Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие дифференциала функции.Содержание книги
Поиск на нашем сайте
Пусть функция Если Учитывая, что для дифференцируемой в точке Заметим, что дифференциал
Точка Установим выражение для дифференциала функции Под дифференциалом независимой переменной будем понимать приращение этой переменной, т.е. В дальнейшем будет показано, что равенство (10) верно и в случае, когда аргумент Дифференцирование сложной функции и обратной функции. Дифференцируемость сложной функции. Теорема 2.1. Пусть функция
Доказательство. Придадим аргументу
Приращению
где
Из дифференцируемости функции
или Замечание 1. Теорема 2.1 последовательно переносится на сложную функцию, являющуюся суперпозицией трёх и большего числа функций. Например, для сложной функции являющейся суперпозицией трёх функций
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.180.210 (0.008 с.) |

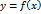 дифференцируема в точке
дифференцируема в точке  , т.е. её приращение в этой точке может быть записано в виде (5). Первое слагаемое в правой части представления (5) имеет вид
, т.е. её приращение в этой точке может быть записано в виде (5). Первое слагаемое в правой части представления (5) имеет вид 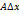 , где
, где 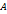 - постоянная, не зависящая от
- постоянная, не зависящая от 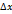 . Если
. Если 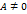 , то
, то 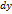 . Итак, для дифференцируемой в точке
. Итак, для дифференцируемой в точке 
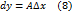
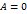 , то дифференциал считают равным нулю.
, то дифференциал считают равным нулю.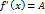 , то равенство (8) можно записать в виде
, то равенство (8) можно записать в виде 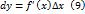 .
.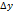 в этой точке
в этой точке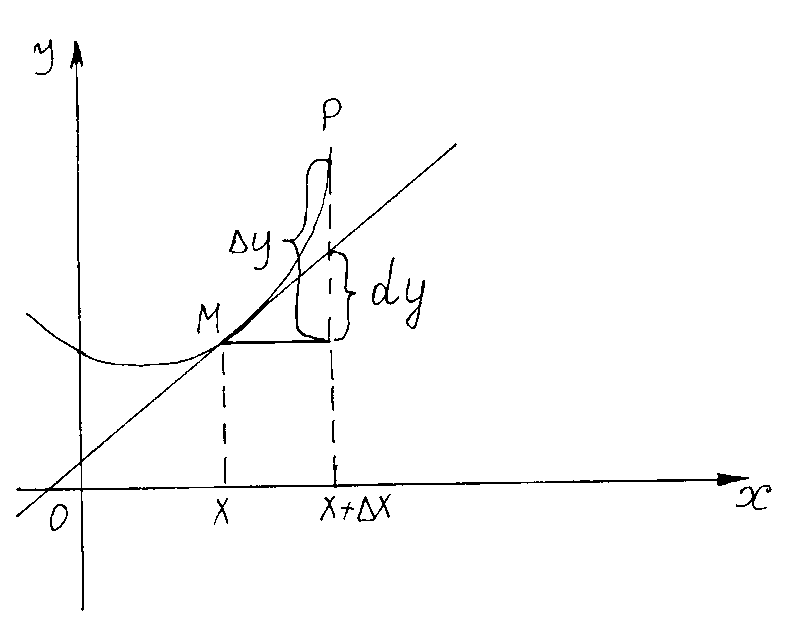
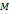 на графике функции имеет координаты
на графике функции имеет координаты 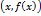 , а точка
, а точка 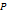 –
– 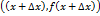 . Тогда приращение
. Тогда приращение 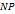 . В то же время из прямоугольного треугольника
. В то же время из прямоугольного треугольника 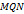 имеем
имеем 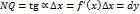 . Очевидно, величина отрезка
. Очевидно, величина отрезка 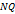 , вообще говоря, отличается от величины
, вообще говоря, отличается от величины 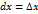 , тогда равенство (9) примет вид:
, тогда равенство (9) примет вид: 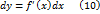 .
.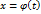 дифференцируема в точке
дифференцируема в точке  , а функция
, а функция 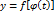 дифференцируема в указанной точке
дифференцируема в указанной точке 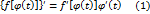
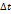 . Этому приращению соответствует приращение
. Этому приращению соответствует приращение 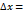
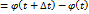 .
.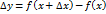 функции
функции 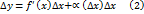
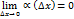 . Поделив равенство (2) на
. Поделив равенство (2) на  , получим
, получим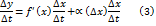
 имеет предел при
имеет предел при 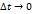 , равный
, равный  . Докажем теперь, что
. Докажем теперь, что 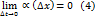 . Из дифференцируемости функции
. Из дифференцируемости функции 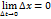 . Т.е.
. Т.е. 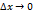 при
при 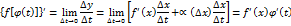
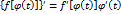 . Теорема 2.1 доказана.
. Теорема 2.1 доказана.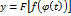 имеем
имеем