
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление отрезка в данном отношении.
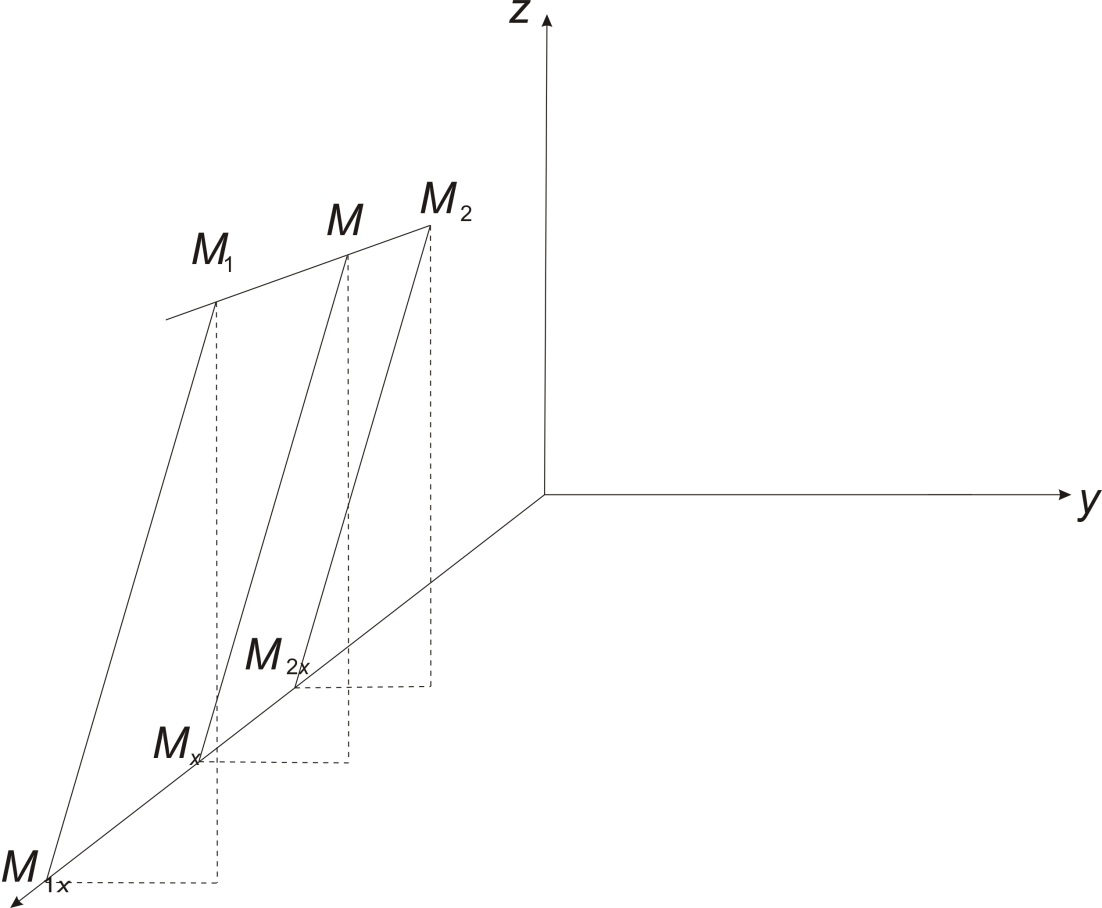
Рассмотрим в пространстве две различные точки Пусть Замечание 1. При изменении направления на прямой, проходящей через точки Введём в пространстве декартову прямоугольную систему координат Выясним, как можно выразить координаты точки
Согласно теореме 1.1 §1 главы 3
Формулы (4) называются формулами деления отрезка в данном отношении 𝜆. Замечание 2. Очевидно, если
Формулы (5) называются формулами деления отрезка пополам.
3. Формула площади треугольника на плоскости. Рассмотрим в плоскости прямоугольную систему координат
Пусть В зависимости от расположения точек 1. Рассмотрим случай 1. Площадь треугольника
Учитывая, что
Аналогично устанавливается справедливость формулы (6) в случаях 2 и 3. Замечание. Аналогичная формула верна и для случая n-угольника
4. Полярная система координат. Во многих задачах математики, наряду с прямоугольными координатами рассматриваются также полярные координаты. Полярные координаты вводятся следующим образом:
Рассмотрим на плоскости некоторую точку Полярными координатами точки Тот факт, что точка Для того, чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат
Пусть точка
Тогда прямоугольные координаты
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.124.232 (0.007 с.) |
 и прямую, проходящую через эти точки. Выберем на этой прямой некоторое направление. Тогда на полученной оси точки
и прямую, проходящую через эти точки. Выберем на этой прямой некоторое направление. Тогда на полученной оси точки 
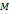 - любая отличная от
- любая отличная от 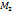 точка указанной оси. Число
точка указанной оси. Число  , где
, где  и
и  - величины направленных отрезков
- величины направленных отрезков  соответственно, называется отношением, в котором точка
соответственно, называется отношением, в котором точка  .
.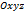 , и пусть в этой системе координат точки
, и пусть в этой системе координат точки  имеют соответственно координаты
имеют соответственно координаты  ,
,  и
и  . Пусть точка
. Пусть точка  , при этом будем считать, что
, при этом будем считать, что  .
. . Пусть
. Пусть 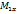 ,
, 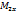 и
и  - основания перпендикуляров, опущенных из точек
- основания перпендикуляров, опущенных из точек  и
и  . Очевидно, что точка
. Очевидно, что точка  в отношении 𝜆, поэтому
в отношении 𝜆, поэтому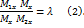
 ,
,  . Тогда из равенств (3) и равенства (2) найдём
. Тогда из равенств (3) и равенства (2) найдём  . Аналогично, проектируя точки
. Аналогично, проектируя точки  и повторяя проведённые выше рассуждения получим следующие формулы нахождения координат точки
и повторяя проведённые выше рассуждения получим следующие формулы нахождения координат точки 
 , то точка
, то точка 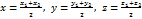 . (5)
. (5)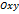 . Пусть вершины треугольника
. Пусть вершины треугольника 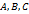 имеют координаты
имеют координаты 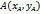 ,
,  ,
,  .
.
 и пусть
и пусть  и
и 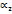 - углы наклона векторов
- углы наклона векторов 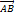 и
и  к оси
к оси 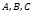 возможны следующие три случая:
возможны следующие три случая: ; 2.
; 2.  ; 3.
; 3. 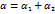 .
.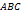 можно найти по формуле
можно найти по формуле .
.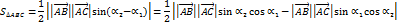
 , получим
, получим
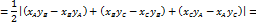
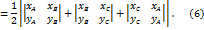
 .
. .
.
 и выходящий из нее луч
и выходящий из нее луч 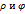 , первое из которых (полярный радиус)
, первое из которых (полярный радиус)  равно расстоянию от полюса
равно расстоянию от полюса  . При этом предполагается, что точка
. При этом предполагается, что точка  .
. ) было взаимно однозначным, считают, что
) было взаимно однозначным, считают, что
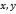 и полярные координаты ρ, 𝜑.
и полярные координаты ρ, 𝜑.
 и полярные координаты ρ, 𝜑, очевидно связаны соотношениями:
и полярные координаты ρ, 𝜑, очевидно связаны соотношениями:  , при этом
, при этом 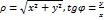 .
.


