
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекция вектора на ось и её свойства.
Пусть дан произвольный вектор Проекцией вектора Проекцию вектора Рис. Углом наклона вектора Теорема 4.1. Проекция вектора Доказательство. Пусть (Рис2) Возможны два случая. 1. Направленный отрезок
2. Направленный отрезок Заметим, что в первом случае (рис 2) Рассмотрим случай 1. Для рассматриваемого случая имеем Из прямоугольного треугольника
Так как, по определению
Тем самым, для случая 1 теорема доказана. Случай 2 рассматривается аналогично. Рассмотрим декартову прямоугольную систему координат Теорема 4.2. Для любого вектора
при этом Доказательство. Приложим вектор
Очевидно, что Из определения величины
Введем обозначения Единственность Числа Теорема 4.3. Пусть в прямоугольной системе координат
Доказательство. Обозначим через
Согласно теореме 1.1 гл.3, величина направленного отрезка Замечание. Если точки Теорема 4.4. При сложении двух векторов Доказательство. Пусть
Из последних равенств вытекает утверждение теоремы. Теорема 4.5. При сложении двух векторов Доказательство. Пусть даны произвольные векторы Пусть в введённой системе координат
Следовательно
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.102.124 (0.009 с.) |
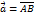 . Пусть
. Пусть 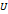 - произвольная ось. Обозначим через
- произвольная ось. Обозначим через 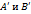 основания перпендикуляров, опущенных на ось
основания перпендикуляров, опущенных на ось  соответственно.
соответственно.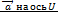 называется величина
называется величина  .
.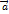 на ось
на ось  . Построение проекции вектора
. Построение проекции вектора  на ось
на ось 
 к оси
к оси  называется угол между двумя лучами, выходящими из произвольной точки
называется угол между двумя лучами, выходящими из произвольной точки  , один из которых имеет направление, совпадающее с направлением вектора
, один из которых имеет направление, совпадающее с направлением вектора  на ось
на ось  – ось, проходящая через начало
– ось, проходящая через начало 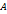 вектора
вектора  и имеющая то же направление, что и ось
и имеющая то же направление, что и ось 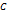 – основание перпендикуляра, опущенного из точки
– основание перпендикуляра, опущенного из точки 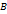 на ось
на ось  , где
, где  - величина направленного отрезка
- величина направленного отрезка  .
.
 имеет направление, совпадающее с направлением оси
имеет направление, совпадающее с направлением оси 
 . (рис.3).
. (рис.3). – угол наклона вектора
– угол наклона вектора  . Четырехугольник
. Четырехугольник  является прямоугольником. Поэтому
является прямоугольником. Поэтому  .
.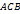 имеем
имеем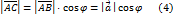
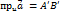 , из равенств (2), (3), (4) находим
, из равенств (2), (3), (4) находим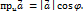
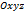 с началом в точке
с началом в точке  и тройку векторов
и тройку векторов 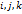 единичной длины, приложенных к точке
единичной длины, приложенных к точке 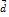 существует единственная тройка чисел
существует единственная тройка чисел  такая, что
такая, что
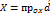 ,
,  ,
,  .
. в точке
в точке 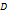 плоскости, параллельные координатным плоскостям
плоскости, параллельные координатным плоскостям  . Точки пересечения этих плоскостей с осями
. Точки пересечения этих плоскостей с осями 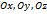 обозначим соответственно
обозначим соответственно 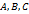 .
.
 . Т.к.
. Т.к.  , мы находим
, мы находим  .
. и из того, что
и из того, что  следует, что
следует, что 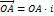 . Так как проекция вектора на ось
. Так как проекция вектора на ось  по определению есть величина
по определению есть величина  . Аналогично доказывается справедливость следующих равенств:
. Аналогично доказывается справедливость следующих равенств:  =
=  =
=  . Учитывая эти равенства в равенстве (6), найдем
. Учитывая эти равенства в равенстве (6), найдем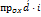 +
+  +
+ 


 , запишем равенство (7) в виде
, запишем равенство (7) в виде 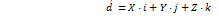
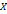 ,
, 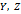 в равенстве (5) называются координатами вектора
в равенстве (5) называются координатами вектора  Тот факт, что
Тот факт, что  .
.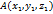 ,
, 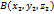 . Тогда координаты
. Тогда координаты  вектора
вектора 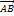 соответственно равны
соответственно равны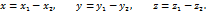
 и
и 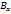 основания перпендикуляров, опущенных из точек
основания перпендикуляров, опущенных из точек  ,
,  , где
, где  – величины направленных отрезков
– величины направленных отрезков 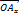 и
и 

 равна
равна  . С другой стороны величина
. С другой стороны величина 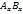 является проекцией вектора
является проекцией вектора 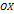 . Следовательно
. Следовательно  вектора
вектора 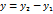 и
и 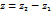 .
. и
и  расположены в плоскости
расположены в плоскости 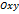 , то для координат вектора
, то для координат вектора  справедливы равенства
справедливы равенства  и
и  и
и 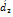 их координаты складываются. При умножении вектора
их координаты складываются. При умножении вектора 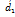 на любое число 𝜆 все его координаты умножаются на это число.
на любое число 𝜆 все его координаты умножаются на это число. ,
,  . Складывая эти равенства и пользуясь свойствами линейных операций, получим
. Складывая эти равенства и пользуясь свойствами линейных операций, получим
 .
.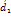 и
и 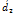 их проекции на произвольную ось складываются. А при умножении вектора
их проекции на произвольную ось складываются. А при умножении вектора  ,
,  . Тогда в силу теоремы 4.4
. Тогда в силу теоремы 4.4 и
и 
 .
.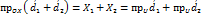 и
и  Теорема доказана.
Теорема доказана.


