
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства определителей.Содержание книги
Поиск на нашем сайте
Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании: Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка. Пусть
Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю. Свойство 2 непосредственно вытекает из определения определителя. Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак. Доказательство свойства 3 приведём для квадратных матриц третьего порядка. Пусть
Пусть
Аналогично проходит доказательство свойства 3, при перестановке любых других строк (столбцов). Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число. Доказательство свойства 4 приведём для случая умножения элементов первой строки, квадратной матрицы третьего порядка, на произвольное число Пусть
Аналогично доказывается свойство 4 для всех остальных случаев. Свойство 5. Если каждый элемент i-й строки (столбца) матрицы Доказательство свойства 5 приведём для случая, когда элементы первой строки квадратной матрицы второго порядка, представлены в виде двух слагаемых. Пусть
Аналогично доказывается свойство 5 и для квадратных матриц третьего порядка. Отметим некоторые следствия, непосредственно вытекающие из перечисленных 5 основных свойств определителя. Следствие 1. Определитель матрицы, имеющей две одинаковые строки (столбца) равен нулю. Доказательство. Пусть
Следствие 2. Если какие-либо две строки (столбца) матрицы пропорциональны, то её определитель равен нулю. Доказательство. Пусть
Будем считать, без ограничения общности, что в матрице
Следствие 3. Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число Доказательство. Пусть
В качестве иллюстрации доказательства, рассмотрим случай, когда к элементам первой строки матрицы
Миноры и алгебраические дополнения. Пусть Число
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.009 с.) |

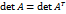 .
. 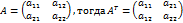
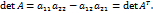

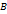 - матрица, полученная из матрицы
- матрица, полученная из матрицы 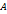 перестановкой мест первых двух строк, т.е.
перестановкой мест первых двух строк, т.е.
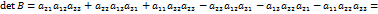
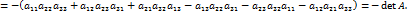
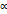 .
.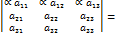
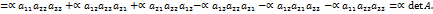
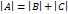 , где элементы матриц
, где элементы матриц 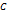 , за исключением элементов -й строки (столбца), совпадают с соответствующими элементами матрицы
, за исключением элементов -й строки (столбца), совпадают с соответствующими элементами матрицы  -х строках (столбцах) матриц
-х строках (столбцах) матриц 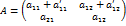 .
.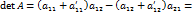
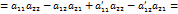
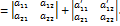
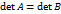 , с другой стороны, в силу свойства 3,
, с другой стороны, в силу свойства 3, 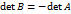 . Следовательно,
. Следовательно, 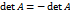 . Из последнего равенства следует, что
. Из последнего равенства следует, что 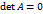 .
.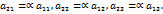
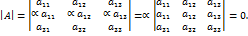
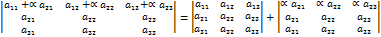 =
= 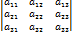
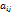 – её элемент, стоящий в позиции
– её элемент, стоящий в позиции 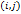 . Вычеркивая из матрицы
. Вычеркивая из матрицы 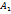 , порядка
, порядка 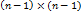 . Определитель матрицы
. Определитель матрицы 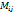 .
.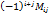 называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 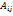 .
.


