
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Элементы математического анализаСодержание книги
Поиск на нашем сайте
Множества. Операции над множествами. Понятие множества относится к первичным, т.е. неопределяемым понятиям. Слова «совокупность», «семейство», «набор» и т.п. – синонимы слова «множество». Примерами множества могут служить множество студентов, присутствующих в данной аудитории, или множество студентов, прогуливающих данную лекцию. Последнее множество, к сожалению, не пустое множество. Множество называется пустым, если оно не содержит ни одного элемента. Обозначается Операции над множествами. Множества
и наоборот
Если Равенство множество обозначается следующим образом Множество Если Тот факт, что Примеры: множество натуральных чисел
Из определения 1 и 2 следует, что множества При этом считается, что Множество элементов Пример. Множество всех положительных чисел
Множество Множество
Очевидно, что если
Разностью множеств
Пусть
Дополнением множества Рассмотрим два множества Отображение 1. 2. Если существует взаимно однозначное отображение множества Тот факт, что множества
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.130.96 (0.009 с.) |

 . Объекты, из которых состоит множество, называются его элементами. Обычно множество обозначают заглавными латинскими буквами
. Объекты, из которых состоит множество, называются его элементами. Обычно множество обозначают заглавными латинскими буквами 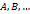 а элементы множества – строчными латинскими буквами. Тот факт, что
а элементы множества – строчными латинскими буквами. Тот факт, что  является элементом множества
является элементом множества 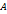 , обозначается следующим образом
, обозначается следующим образом 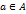 . И читается «
. И читается «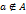
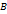 называются равными, если
называются равными, если
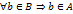
 .
.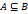 .
.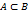 .
.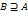 .
.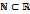
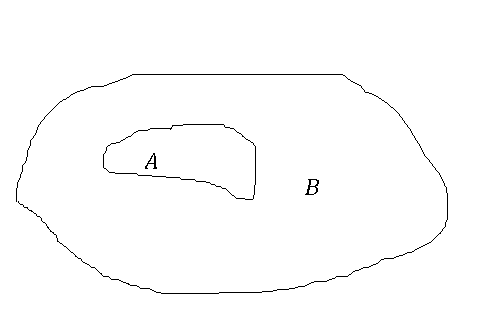
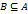 .
. из некоторого множества
из некоторого множества 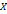 , обладающих некоторым свойством
, обладающих некоторым свойством 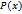 будем обозначать следующим образом
будем обозначать следующим образом 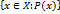 .
.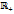 можно записать следующим образом
можно записать следующим образом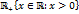
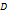 называется объединением множеств
называется объединением множеств 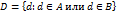
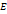 называется пересечением множеств
называется пересечением множеств 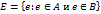
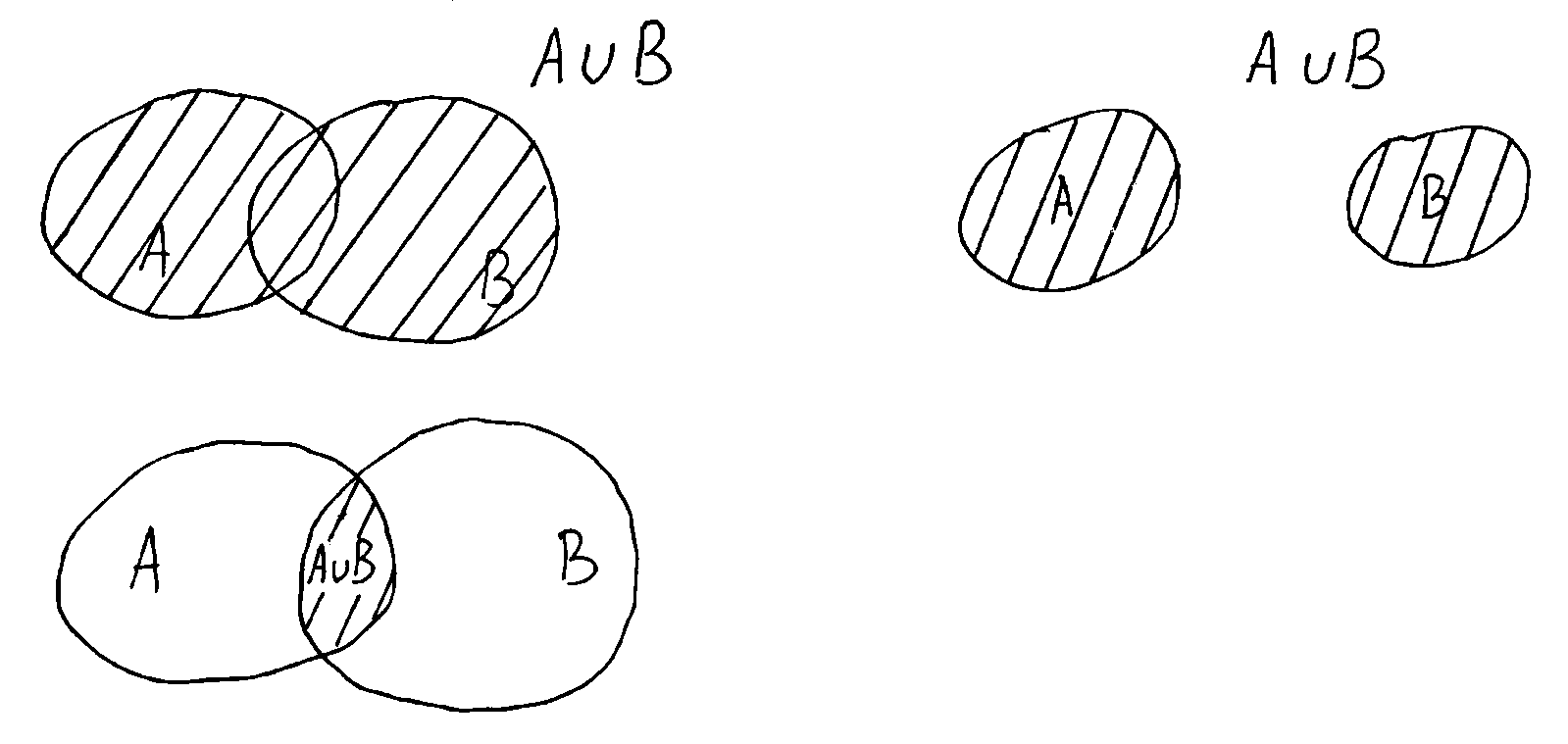
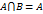 .
.
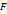 , что каждый элемент множества
, что каждый элемент множества 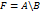 .
.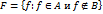
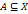 .
. . Обозначение
. Обозначение 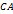 или
или 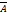 .
. множества
множества 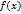 . Тогда
. Тогда 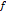 называется отображением множества
называется отображением множества 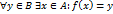
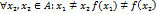
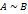 .
.


