
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение определителя по строке (столбцу)Содержание книги
Поиск на нашем сайте
Теорема 4.1. Определитель квадратной матрицы равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения. В качестве иллюстрации докажем, что определитель любой квадратной матрицы третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения. Пусть.
Рассмотрим сумму произведений элементов первой строки на их алгебраическое дополнение
Легко заметить, что правая часть равенства (3) равна определителю матрицы Понятие определителя квадратной матрицы любого порядка Приведённая теорема 4.1 может быть положена в основу последовательного введения по индукции определителя четвёртого, пятого и всех последующих порядков. Предположим, что уже введено понятие определителя Назовём определителем квадратной матрицы
Заметим, что в правой части равенства (4) стоит сумма произведений элементов первой строки на их алгебраические дополнения. Можно доказать, если взять сумму произведений элементов любой другой строки (столбца) матрицы Заметим также, что при Такая схема введения определителя любого порядка изложена в книге В.А. Ильин, Э.Г. Позняк «Линейная алгебра» (М: Физматлит, 2001). Там же доказано, что определители любого порядка Заметим, что теоретически, определитель любой квадратной матрицы порядка В дальнейшем приведём метод Гаусса, существенно облегчающий вычисление определителя. Теорема 4.2. Определитель любой верхней треугольной (нижней треугольной) матрицы равен произведению диагональных элементов. Доказательство. Рассмотрим случай верхней треугольной матрицы (Случай нижней треугольной матрицы рассматривается аналогично).
Разложив определитель
Раскладывая полученный определитель
Теорема 4.2. доказана. Следствие из теоремы 4.2. Определитель любой диагональной матрицы равен произведению диагональных элементов. Данное следствие непосредственно вытекает из теоремы 4.2. и того факта, что любая диагональная матрица является как верхней треугольной, так и нижней треугольной. Теорема 4.3. ** Определитель произведения квадратных матриц Изящное доказательство этой теоремы можно найти в книге В.А. Ильин, Г.Д. Ким «Линейная алгебра и аналитическая геометрия». Теорема 4.4. (О фальшивом разложении определителя). Сумма произведений элементов одной строки (столбца) квадратной матрицы, на алгебраические дополнения элементов другой её строки (столбца) равна нулю. Доказательство. Пусть
Рассмотрим матрицу
Определитель матрицы
Вычисление определителя. Во многих задачах линейной алгебры возникает необходимость вычисления определителя. Среди различных методов вычисления определителя особое место занимает метод Гаусса. Суть метода Гаусса вычисления определителя состоит в следующем: 1. Привести элементарными преобразованиями данную квадратную матрицу к треугольному виду. При этом такие преобразования либо не изменяют определителя матрицы, либо изменяют его контролируемым образом; 2. Вычислить определитель треугольной матрицы; 3. Восстановить исходный определитель.
Обратная матрица Условие обратимости. Матрица Так как равенство
Квадратная матрица Теорема 5.1. (Критерий обратимости) Матрица Доказательство. Пусть Пусть теперь матрица
где Рассмотрим матрицу
Из последнего равенства следует, что Совершенно аналогично доказывается, что
Теорема 5.1 доказана. Теорема 5.2. (О единственности обратной матрицы) Если Доказательство. Т.к. матрица Пусть Умножая равенство С другой стороны
Сравнивая равенства (1) и (2) приходим к выводу Теорема 5.2 доказана. В качестве примера найдём обратную к матрице Как уже известно, обратную матрицу
Проверить самостоятельно, что Теорема 5.3. (обратимость призведения двух невырожденных матриц) Пусть
Доказательство. В силу теоремы 4.3 Рассмотрим матрицу Рассмотрим теперь матрицу
Из равенств (3), (4) и определения обратной матрицы следует, что Обратная к невырожденной диагональной матрице. Пусть Тогда
Легко проверить, что обратной к матрице
(Проверить самостоятельно). Замечание. Из теоремы 4.3 непосредственно вытекает справедливость равенства
Ранг матрицы. Понятие ранга матрицы. Пусть Для обозначения минора будем пользоваться символом Рангом ненулевой матрицы называется максимальный порядок ненулевых миноров этой матрицы. Ранг нулевой матрицы по определению считается равным нулю.
Ранг матрицы будем обозначать символами Из определения ранга матрицы вытекают следующие факты: 1.Ранг матрицы не превосходит её размеров: есл 2.Равенство Пусть Теорема 6.1. При транспонировании матрицы её ранг не изменяется. Доказательство. Справедливость приведенной теоремы вытекает из следующих двух фактов: 1. Определители транспонированных матриц равны; 2. При транспонировании базисные строки матрицы Теорема 6.2. Элементарные преобразования матрицы не изменяют её ранга. Справедливость теоремы непосредственно вытекает из определения ранга, так как, при элементарных преобразованиях матрицы, любой её ненулевой минор преобразуется в ненулевой минор. Теорема 6.3. Ранг трапециевидной матрицы равен числу её ненулевых строк. Доказательство. Пусть матрица Рассмотрим минор В силу теоремы 4.2 Пусть Доказательство теоремы 6.3, для верхних травециевидных матриц остальных трех типов проводится аналогично. Метод Гаусса вычисления ранга. Теоретическую основу этого метода составляют, доказанные выше, теоремы 6.2 и 6.3. Суть метода Гаусса вычисления ранга матрицы состоит в приведении этой матрицы элементарными преобразованиями к верхней трапециевидной форме и подсчете ненулевых строк полученной трапециевидной матрицы.
|
|||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.117 (0.008 с.) |



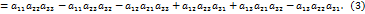
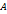 .
.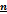 .
.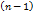 -го порядка. Пусть
-го порядка. Пусть 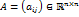 Минором каждого элемента
Минором каждого элемента 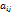 матрицы
матрицы 
 .
. разложение (4) совпадает с разложением определителя третьего порядка по первой строке.
разложение (4) совпадает с разложением определителя третьего порядка по первой строке. обладают теми же свойствами, что определители второго и третьего порядков.
обладают теми же свойствами, что определители второго и третьего порядков.
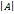 по первому столбцу, получим
по первому столбцу, получим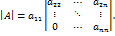
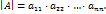
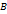 равен произведению определителей матриц-сомножителей, т.е.
равен произведению определителей матриц-сомножителей, т.е. 

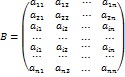
 , т.к. в этой матрице две одинаковые строки. С другой стороны, по теореме 4.1. определитель матрицы
, т.к. в этой матрице две одинаковые строки. С другой стороны, по теореме 4.1. определитель матрицы 
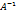 называется обратной к матрице
называется обратной к матрице  , где
, где 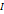 - единичная матрица. Матрица
- единичная матрица. Матрица  одинакового размера, то обратимой может быть лишь квадратная матрица. Однако, не каждая квадратная матрица обратима.
одинакового размера, то обратимой может быть лишь квадратная матрица. Однако, не каждая квадратная матрица обратима. , и невырожденной, если
, и невырожденной, если 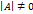 .
.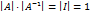 . Следовательно
. Следовательно 
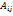 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 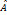 называется присоединённой или взаимной к матрице
называется присоединённой или взаимной к матрице  является обратной к матрице
является обратной к матрице 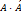 . В позиции
. В позиции 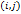 матрицы
матрицы 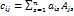 ,
, . Из теоремы 4.4. и определения определителя n-го порядка следую, что
. Из теоремы 4.4. и определения определителя n-го порядка следую, что 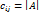 при
при  и
и  при
при  . Следовательно
. Следовательно .
.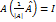 .
.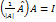 , т.е.
, т.е. 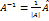 .
.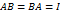 . Единственность обратной матрицы будет доказана, если
. Единственность обратной матрицы будет доказана, если 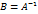 .
.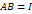 слева на матрицу
слева на матрицу 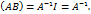 (1)
(1) =
=  . (2)
. (2)
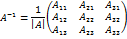

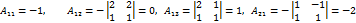
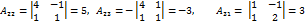
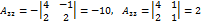
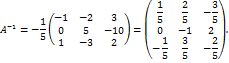
 квадратные невырожденные матрицы порядка
квадратные невырожденные матрицы порядка 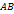 обратима и при этом
обратима и при этом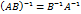
 . Т.е. матрица
. Т.е. матрица 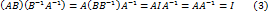
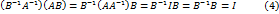
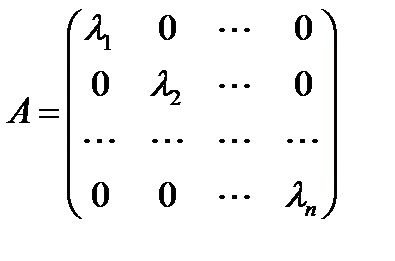 .
.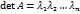 . Из условия невырожденности матрицы
. Из условия невырожденности матрицы 

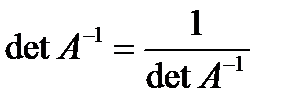 (проверить самостоятельно).
(проверить самостоятельно).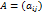 - произвольная матрица размера
- произвольная матрица размера 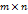 ,
, 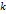 - произвольное натуральное число, удовлетворяющее неравенству
- произвольное натуральное число, удовлетворяющее неравенству 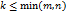 . Выберем в матрице
. Выберем в матрице 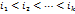 и
и  соответственно. Элементы матрицы
соответственно. Элементы матрицы 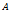 , стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка, расположенным в строках с номерами
, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка, расположенным в строках с номерами  и столбцах с номерами
и столбцах с номерами  .
. или
или 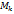 .
. .
.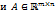 , то
, то 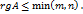
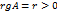 равносильно выполнению двух условий: а) в матрице A существует ненулевой минор порядка r; б) любой минор более высокого порядка (если такой существует) равен нулю.
равносильно выполнению двух условий: а) в матрице A существует ненулевой минор порядка r; б) любой минор более высокого порядка (если такой существует) равен нулю.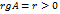 . Любой ненулевой минор порядка
. Любой ненулевой минор порядка  называется базисным минором. Строки и столбцы матрицы
называется базисным минором. Строки и столбцы матрицы  , а базисные столбцы – базисными строками.
, а базисные столбцы – базисными строками.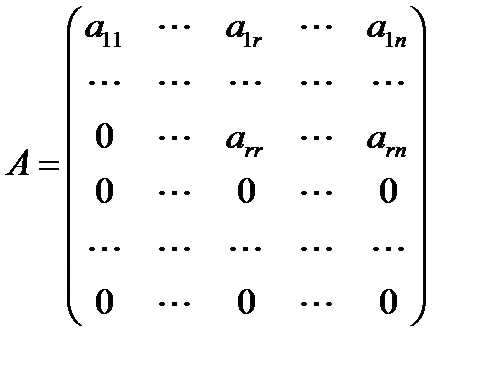 .
. порядка
порядка 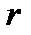 , расположенный в левом верхнем углу матрицы
, расположенный в левом верхнем углу матрицы  .
. .
.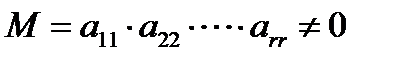 .
.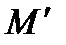 - любой минор, порядок которого больше
- любой минор, порядок которого больше 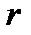 . Так как, в матрице
. Так как, в матрице  всего
всего  . Следовательно
. Следовательно  .
.


