
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация линий второго порядка.Содержание книги
Поиск на нашем сайте В зависимости от знака величины 1. 2. 3. Нами доказано, что любое уравнение линии второго порядка
Очевидно, что при преобразовании координат меняется только вид уравнения линии второго порядка. Поэтому мы можем вместо общего уравнения линии второго порядка исследовать уравнение более простого вида, а именно уравнение (47). 1) Рассмотрим линии эллиптического типа, т.е.
Рассмотрим два случая а)
Т.к.
Очевидно, что последнему уравнению не удовлетворяют координаты никакой точки плоскости. Оно называется уравнением мнимого эллипса. б)
Т.к.
Т.е. в этом случае уравнение (47) определяет эллипс. (Рассмотреть случай Случаи 2) Гиперболический тип. а)
Так как
Последнее уравнение является каноническим уравнением гиперболы. б)
Последнему уравнению удовлетворяют координаты точек, расположенных на пересекающихся прямых в) Так как
Что является уравнением гиперболы, сопряжённой к гиперболе
Все оставшиеся случаи получаются из рассмотренных случаев а, б, в. 3. Параболический тип. Если
Так как выражение
Из этого уравнения имеем
Перенесём начало координат параллельно оси
И уравнение (50) примет вид
где Рассмотрим два случая. а)
Перенесём начало координат параллельно оси
б)
Если
Уравнение (54) в свою очередь можно записать в виде Если Наконец, если В заключении сформулируем следующую теорему, справедливость которой следует из проведённого выше рассуждений. Теорема 4.1. Пусть в прямоугольной системе координат задано общее уравнение линии второго порядка
Тогда существует такая прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов: 1) 2) 3) 4) 5) 6) 7) 8) 9)
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

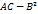 общее уравнение линии второго порядка разделяются на следующие три типа:
общее уравнение линии второго порядка разделяются на следующие три типа: эллиптический тип
эллиптический тип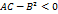 гиперболический тип
гиперболический тип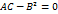 параболический тип.
параболический тип.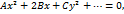 при
при  путём преобразования координат (параллельный перенос и поворот на определённый угол
путём преобразования координат (параллельный перенос и поворот на определённый угол 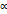 ) можно привести к виду
) можно привести к виду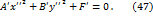
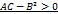 . Выше было доказано, что
. Выше было доказано, что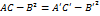 , т.е. величина
, т.е. величина 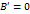 , то
, то  , и следовательно,
, и следовательно,  .
. ,
,  ,
, 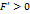 . Тогда из уравнения (47) имеем
. Тогда из уравнения (47) имеем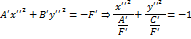
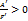 и
и  , то обозначая
, то обозначая 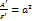 и
и 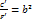 , получим
, получим
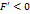 . Тогда из уравнения (47) имеем
. Тогда из уравнения (47) имеем
 и
и 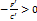 , обозначая
, обозначая  ,
, 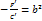 , получим
, получим
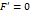 )
)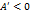 ,
,  ,
,  . Рассмотрим следующие возможные случаи:
. Рассмотрим следующие возможные случаи: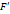 в правую часть уравнения и разделим на него, получим
в правую часть уравнения и разделим на него, получим
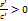 , то, обозначая
, то, обозначая 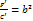 , получим
, получим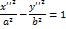
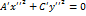 . Обозначая
. Обозначая 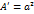 ,
, , получим
, получим  или
или 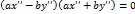 .
.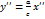 и
и 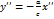 . Таким образом, в данном случае, уравнение (47) определяет пару пересекающихся прямых.
. Таким образом, в данном случае, уравнение (47) определяет пару пересекающихся прямых.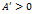 ,
, 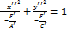 .
. , то обозначая
, то обозначая 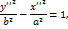


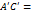
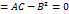 . Т.е либо
. Т.е либо 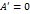 , либо
, либо 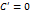 . Пусть
. Пусть 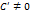 . Тогда из уравнения (49) найдем
. Тогда из уравнения (49) найдем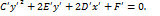
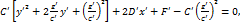 или
или
 в точку
в точку 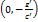 и перейдём к новым координатам
и перейдём к новым координатам 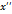 и
и  , тогда
, тогда

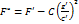 .
.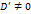 . Тогда уравнение (51) можно записать в виде
. Тогда уравнение (51) можно записать в виде
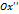 в точку
в точку  , получим
, получим 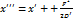 ,
, 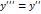 . Учитывая последние равенства в уравнении (52), получим
. Учитывая последние равенства в уравнении (52), получим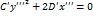 или
или 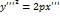 , где
, где 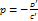 .
.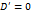 , тогда
, тогда
 и
и 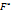 имеют разные знаки, то уравнение (53) можно записать в следующем виде:
имеют разные знаки, то уравнение (53) можно записать в следующем виде: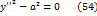 где
где  .
. . Это уравнение определяет пару параллельных прямых
. Это уравнение определяет пару параллельных прямых  и
и  .
.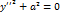 , где
, где  . Очевидно последнему уравнению не удовлетворяют координаты никакой точки плоскости. Оно называется уравнением пары мнимых параллельных прямых.
. Очевидно последнему уравнению не удовлетворяют координаты никакой точки плоскости. Оно называется уравнением пары мнимых параллельных прямых.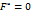 , то уравнение (53) примет вид
, то уравнение (53) примет вид 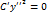 или
или 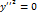 . Последнее уравнение определяет ось
. Последнее уравнение определяет ось  и оно называется уравнением пары совпадающих прямых.
и оно называется уравнением пары совпадающих прямых.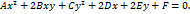
 – эллипс;
– эллипс;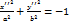 - мнимый эллипс;
- мнимый эллипс; - пара мнимых пересекающихся прямых;
- пара мнимых пересекающихся прямых; - гипербола;
- гипербола;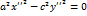 - пара пересекающихся прямых;
- пара пересекающихся прямых;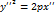 парабола;
парабола;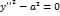 - пара параллельных прямых;
- пара параллельных прямых;


