Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия пересечения, коллинеарности и ортогональности двух прямых. Угол между двумя пересекающимися прямыми.Содержание книги
Поиск на нашем сайте
Условие коллинеарности двух прямых. Пусть прямые
Две прямые будем называть коллинеарными, если они либо параллельны, либо совпадают (сливаются). Очевидно, что прямые, определяемые уравнениями (15) и (16) коллинеарны тогда и только тогда, когда коллинеарны их нормальные векторы
В случае
Равенство (19) является условием коллинеарности прямых Замечание. В равенстве (17) мы предполагаем, что
Рассмотрим определитель
Если прямые Заметим, что
Данная система имеет единственное решение при условии, что
Итак, если прямые, лежащие в плоскости Если выполнено условие (19), то прямые Пусть прямые Тогда справедливы равенства
Пользуясь равенствами (23), получим
Могут представиться два случая. 1.
Следовательно в случае, когда
является условием параллельности прямых 2. Пусть теперь
Итак, мы получили следующее условие слияния двух прямых
Заметим, что при выполнении условия (25) система линейных уравнений (20) не имеет решений, а при выполнении условия (26) имеет бесконечное множество решений. Условие ортогональности двух прямых. Любые две пересекающиеся в одной точке прямые Найдём угол между векторами Пусть прямые
Учитывая в этой формуле, что
получим
В частности, если угол
Пусть теперь прямые
Запишем уравнения (27) и (28) в виде
Уравнения (31) и (32) являются общими уравнениями прямых
Из условия (26) получим условие слияния двух прямых
Из формулы (27) получим формулу для определения угла
Из условия (28) получим условие ортогональности прямых Рассмотрим теперь случай, когда прямые
Из уравнений (37) и (38) получим
Уравнения (39) и (40) являются общими уравнениями прямых
1. Условие коллинеарности 2. Условие параллельности 3. Условие слияния 4. Формула для вычисления угла 5. Условие ортогональности Приведём ещё одну формулу для нахождения угла между двумя прямыми. Пусть прямые
Пусть
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.130.151 (0.009 с.) |

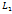 и
и 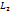 заданные их общими уравнениями
заданные их общими уравнениями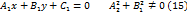
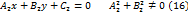
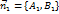 ,
, 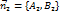 . Коллинеарность векторов
. Коллинеарность векторов 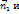
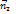 означает существует такого действительного число 𝜆, что
означает существует такого действительного число 𝜆, что 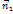
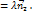 Следовательно прямые, заданные уравнениями (15) и (16), коллинеарны тогда и только тогда, когда выполнены равенства:
Следовательно прямые, заданные уравнениями (15) и (16), коллинеарны тогда и только тогда, когда выполнены равенства: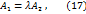
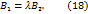
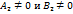 , равенства (17) и (18) могут быть записаны в виде:
, равенства (17) и (18) могут быть записаны в виде: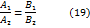
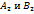 обращается в ноль, например
обращается в ноль, например 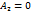 , то из равенства (17) имеем, что и
, то из равенства (17) имеем, что и 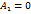 .
.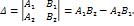
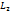 не коллинеарны, то нарушено равенство (19), тогда очевидно определитель
не коллинеарны, то нарушено равенство (19), тогда очевидно определитель 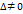 .
. является определителем основной матрицы системы линейных алгебраических уравнений
является определителем основной матрицы системы линейных алгебраических уравнений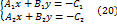
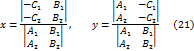
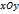 неколлинеарны, то координаты точки их пересечения находятся по формулам (21).
неколлинеарны, то координаты точки их пересечения находятся по формулам (21).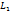 и
и  коллинеарны, т.е. они либо параллельны и не имеют ни одной общей точки, либо эти прямые совпадают.
коллинеарны, т.е. они либо параллельны и не имеют ни одной общей точки, либо эти прямые совпадают. , т.е. положим, что
, т.е. положим, что 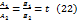
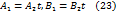 . Рассмотрим произвольную точку
. Рассмотрим произвольную точку 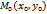 , лежащую на прямой
, лежащую на прямой 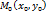 удовлетворяют уравнению
удовлетворяют уравнению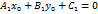
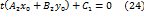
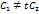 , тогда из равенства (24) найдём
, тогда из равенства (24) найдём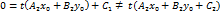 . Из последних соотношений имеем
. Из последних соотношений имеем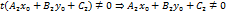
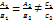 , произвольная точка
, произвольная точка 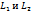 нет общих точек. Следовательно, условие
нет общих точек. Следовательно, условие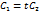 , где
, где 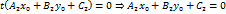 , т.е. точка
, т.е. точка 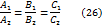
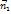 и
и 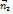 этих прямых.
этих прямых.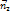
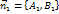 ,
, 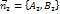 . Обозначим через
. Обозначим через 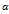 угол между векторами
угол между векторами 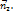 Косинус этого угла может быть вычислен по формуле:
Косинус этого угла может быть вычислен по формуле: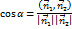
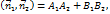
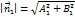 ,
, 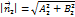 ,
,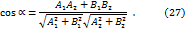
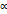 прямой, то
прямой, то 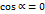 и мы получим условие ортогональности прямых
и мы получим условие ортогональности прямых  (28)
(28)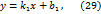
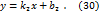
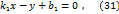
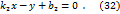
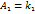 ,
, 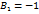 ,
, 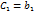 ,
, 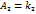 ,
, 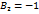 ,
, 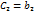 . При этом из условия (25) получим условие параллельности прямых
. При этом из условия (25) получим условие параллельности прямых 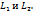
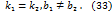
 .
. между прямыми
между прямыми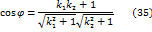
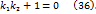
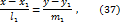
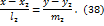
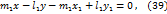
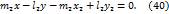
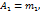
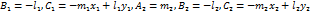 . Тогда из условий (25), (26), (27), (28) получим
. Тогда из условий (25), (26), (27), (28) получим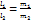 .
.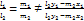 .
.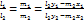 .
.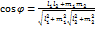 .
.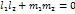 .
.
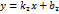
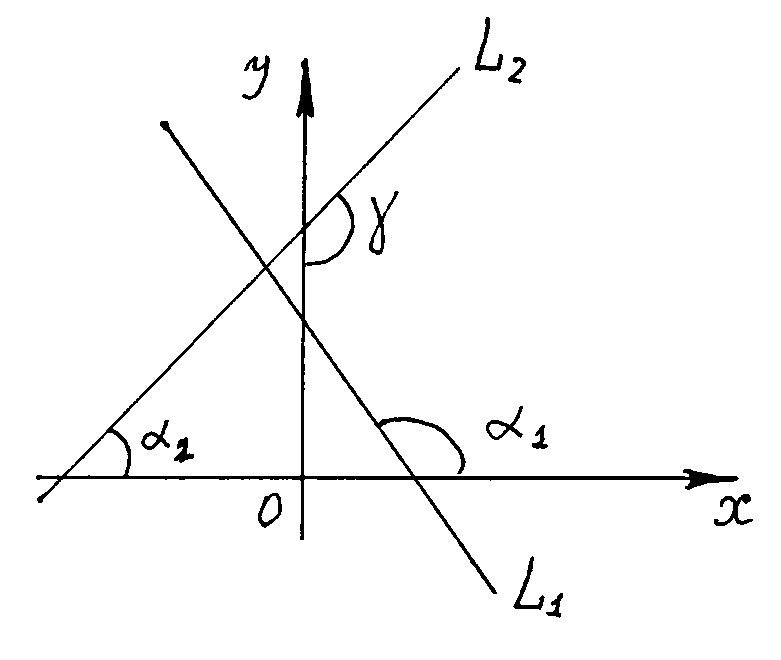
 - угол между прямыми
- угол между прямыми 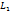 до прямой
до прямой 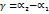 , либо
, либо 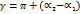 , либо
, либо 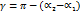 . Но во всех указанных случаях
. Но во всех указанных случаях 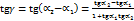 . Учитывая в последнем равенстве, что
. Учитывая в последнем равенстве, что 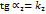 ,
, 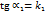 , получим
, получим