
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 7. Теоремы о дифференцируемых функциях и их приложенияСодержание книги
Поиск на нашем сайте Локальный экстремум функции. 1. Теорема Ферма. (Необходимое условие локального экстремума). Определение 1.1. Точка Если в определении 1.1 вместо неравенства Определение 1.1. (Теорема Ферма о необходимом условии локального экстремума). Пусть функция Если функция Доказательство. Рассмотрим случай, когда функция
Т.к. функция
По определению правой производной
Т.к.
Итак, мы доказали, что Аналогично рассматривается случай локального минимума. Теорема 1.1 доказана. Теорема 1.1 имеет простой геометрический смысл: если дифференцируемая в точке Теорема Ролля. Теорема 1.2. Если функция Доказательство. Так как функция
Возможны два случая: 1. В первом случае Во втором случае, т.к. Теорема Ролля имеет простой геометрический смысл: если Теорема Лагранжа. Теорема 1.3. Если функция
Формула (4) называется формулой Лагранжа. Доказательство. Рассмотрим функцию
Из равенства (6) следует, что
Теорема доказана. Теорема Лагранжа также имеет простой геометрический смысл. Прежде всего заметим, что величина
Теорема 1.4. Если функция Доказательство. Рассмотрим произвольные две точки
Теорема 1.4 имеет простой геометрический смысл: если касательная к графику функции
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

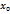 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  , если существует такая
, если существует такая  окрестность точки
окрестность точки  справедливо неравенство
справедливо неравенство 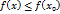
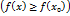 .
.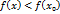
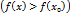 , то такая точка
, то такая точка 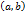 и пусть в точке
и пусть в точке 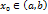 локальный экстремум. Тогда если
локальный экстремум. Тогда если 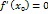 .
. , т.е.
, т.е.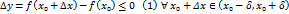
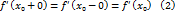

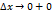 , то
, то 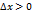 , следовательно, из неравенства (1) имеем
, следовательно, из неравенства (1) имеем 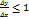 . Тогда такому неравенству удовлетворяет
. Тогда такому неравенству удовлетворяет 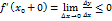 , т.е.
, т.е. 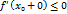 . Рассмотрим теперь
. Рассмотрим теперь 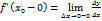 . Т.к.
. Т.к.  , то
, то 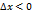 , тогда из неравенства (1) следует
, тогда из неравенства (1) следует  . Следовательно
. Следовательно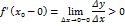
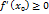 и
и 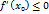 , что возможно только в случае
, что возможно только в случае 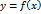 в точке
в точке  параллельна оси
параллельна оси  .
.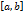 и имеет производную во всех точках интервала
и имеет производную во всех точках интервала 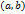 , кроме того
, кроме того 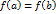 , то внутри сегмента найдётся такая точка
, то внутри сегмента найдётся такая точка 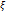 , производная
, производная  в которой равна нулю.
в которой равна нулю. , что
, что 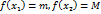 . При этом
. При этом

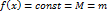 . Поэтому производная
. Поэтому производная  функции
функции 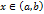 , т.е. для этого случая теорема доказана.
, т.е. для этого случая теорема доказана.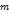 или
или 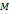 не принимается на концах сегмента
не принимается на концах сегмента 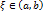 , в которой функция
, в которой функция 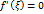 . Теорема 1.2 доказана.
. Теорема 1.2 доказана.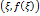 , в которой касательная к графику параллельна
, в которой касательная к графику параллельна 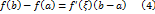
 , определённую на сегменте
, определённую на сегменте 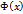 выполнены все условия теоремы Ролля. Действительно, функция
выполнены все условия теоремы Ролля. Действительно, функция  и
и  . Функция
. Функция  и
и 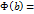
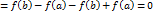 , т.е.
, т.е. 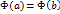 . Тогда по теореме Ролля существует точка
. Тогда по теореме Ролля существует точка  . Вычислим
. Вычислим 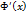 .
.
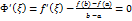 или
или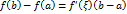
 является угловым коэффициентом секущей, проходящей через точки
является угловым коэффициентом секущей, проходящей через точки  и
и  кривой
кривой 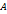 и
и 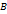 найдётся точка
найдётся точка 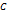 , касательная в которой параллельна секущей
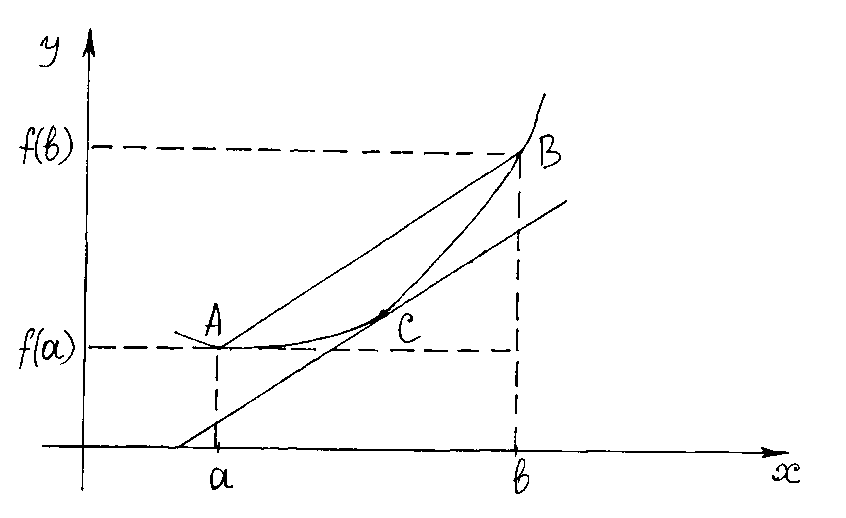
, касательная в которой параллельна секущей 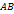 .
.
 указанного интервала
указанного интервала 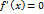 , то функция
, то функция  , поэтому функция
, поэтому функция 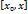 . Тогда по теореме Лагранжа
. Тогда по теореме Лагранжа 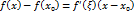 , где
, где 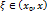 . Т.к.
. Т.к. 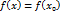 . Т.е. значения функции
. Т.е. значения функции 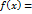
 . Теорема доказана.
. Теорема доказана.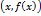 , где
, где 


