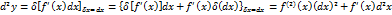Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциалы высших порядков.
В данном разделе мы будем использовать для обозначения дифференциала наряду с символом Как уже известно, для первого дифференциала дифференцируемой в данной точке
Предположим, что правая часть равенства (3) является функцией аргумента Для этого достаточно потребовать, чтобы функция
от обеих частей равенства (3). Определение 5.1. Значение Итак по определению Предположим, что уже введён дифференциал Определение 5.2. Значение Итак, по определению При вычислении второго и последующих дифференциалов следует существенно различать два случая: 1) когда аргумент В случае, когда
Итак, в случае, когда аргумент По аналогии устанавливается, что в случае, когда аргумент
Таким образом, для случая, когда аргумент
Иной вид имеют представления второго и последующих дифференциалов в случае, когда аргумент Пусть функция
Из последнего равенства находим
Т.е Сравнивая равенства (5) и (6) мы видим, что в отличии от первого дифференциала, второй дифференциал не обладает свойством инвариантности формы. Тем более не обладают свойством инвариантности формы последующие дифференциалы.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.136 (0.005 с.) |
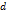 также символ
также символ  .
. функции
функции 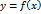 справедливо равенство
справедливо равенство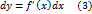
 . При этих предположениях мы можем рассмотреть дифференциал
. При этих предположениях мы можем рассмотреть дифференциал
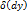 дифференциала от первого дифференциала (3) взятое при
дифференциала от первого дифференциала (3) взятое при 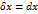 , называется вторым дифференциалом функции
, называется вторым дифференциалом функции 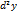 .
.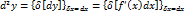 .
. порядка
порядка  и что функция
и что функция  является
является  раз дифференцируемой в данной точке
раз дифференцируемой в данной точке  дифференциала
дифференциала 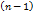 -го порядка
-го порядка 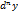 .
.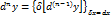 .
.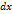 не зависит от
не зависит от 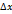 . При этом мы имеем
. При этом мы имеем 
 . Тогда
. Тогда