
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второе достаточное условие экстремума.
В некоторых случаях исследование знака первой производной слева и справа от точки возможного экстремума затруднено. В таких случаях целесообразно использовать второе достаточное условие экстремума. При этом приходится усиливать условие, накладываемое на функцию Теорема 4.2. (Второе достаточное условие экстремума) Пусть функция Доказательство. По определению, вторая производная функции
Т.к.
По условию
или
Т.к. 1) 1) Если 2) Если Пусть теперь
Экстремум функции, не дифференцируемой в данной точке. При доказательстве теоремы 4.1 мы пользовались теоремой Лагранжа на сегменте Теорема 4.3. Пусть функция
Пример.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 55; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.154.208 (0.005 с.) |
 . Справедлива следующая теорема:
. Справедлива следующая теорема: конечную вторую производную
конечную вторую производную  . При этом
. При этом 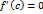 . Тогда функция
. Тогда функция  и локальный минимум, если
и локальный минимум, если  . (Рассмотрим случай
. (Рассмотрим случай 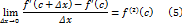
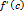 , из равенства (5) получим
, из равенства (5) получим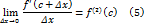
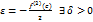 такое, что для всех
такое, что для всех  справедливы неравенства
справедливы неравенства
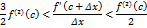
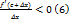 для всех
для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 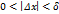 . Рассмотрим два случая
. Рассмотрим два случая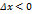 2)
2)  .
. и из неравенства (6) имеем
и из неравенства (6) имеем  , т.е. производная функции
, т.е. производная функции 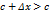 и из неравенства (6) имеем
и из неравенства (6) имеем 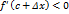 , т.е. производная функции отрицательна справа от точки
, т.е. производная функции отрицательна справа от точки  , тогда
, тогда  ,
, 
 , следовательно функция
, следовательно функция 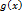 имеет в точке
имеет в точке  , в случае, когда рассматривался интервал
, в случае, когда рассматривался интервал 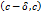 и
и  . Но в теореме Лагранжа вовсе не требуется, чтобы функция
. Но в теореме Лагранжа вовсе не требуется, чтобы функция  положительна (соответственно отрицательна) слева от точки
положительна (соответственно отрицательна) слева от точки 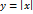 . Эта функция непрерывна на всей бесконечной прямой и дифференцируема в каждой точке, за исключением одной точки
. Эта функция непрерывна на всей бесконечной прямой и дифференцируема в каждой точке, за исключением одной точки 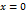 , причём
, причём  при
при 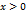 и
и  при
при  . Теорема 4.1 к этой функции неприменима, а согласно теореме 4.3 она имеет минимум в точке
. Теорема 4.1 к этой функции неприменима, а согласно теореме 4.3 она имеет минимум в точке 


