
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 8. Неопределённый интеграл.
Понятие первообразной функции и неопределённого интеграла. Понятие первообразной функции. Определение 1.1. Функция
Замечание. В определении 1.1 интервал Примеры: функция Если функция Следующая теорема устанавливает связь между различными первообразными одной и той же функции. Теорема 1.1. Если Доказательство. Обозначим через Следствие из теоремы 1.1. Если Неопределённый интеграл. Определение 1.2. Совокупность всех первообразных функции
Знак Если
где Равенство (1) непосредственно следует из следствия теоремы (1). Основные свойства неопределённого интеграла. 1.
2. 3. Постоянный множитель можно вынести из-под знака интеграла, т.е.
где Действительно, если
4. Неопределённый интеграл от суммы или разности двух функций равен соответственно сумме или разности неопределённых интегралов этих функций, т.е.
Действительно, пусть
Так как
Таблица основных интегралов. Приведённые ниже интегралы принято называть табличными интегралами. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Справедливость всех приведённых формул, за исключением формул 4, 12, 13, непосредственно следует из определения неопределённого интеграла и таблицы производных элементарных функций. Сделаем замечания в отношении формул 4, 12 и 13. Формула 4 справедлива для любого интервала, не содержащего точки Докажем равенство 12. Рассмотрим два случая 1)
1.
Следовательно
Рассмотрим теперь функцию
Следовательно справедливо
на полупрямой Если
Т.е.
на интервале Справедливость равенства (12) доказана. Справедливость равенства (13) проверить самостоятельно.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.132 (0.022 с.) |
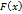 называется первообразной функцией функции
называется первообразной функцией функции  на интервале
на интервале 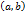 , если всюду на интервале
, если всюду на интервале  существует производная
существует производная  и эта производная
и эта производная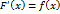 .
. , либо на одну из бесконечных полупрямых
, либо на одну из бесконечных полупрямых 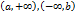 .
. является первообразной функции
является первообразной функции  на интервале
на интервале  , так как всюду на этом интервале
, так как всюду на этом интервале  ; функция
; функция 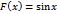 является первообразной функции
является первообразной функции  на бесконечной прямой
на бесконечной прямой 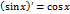 ; функция
; функция  является первообразной функции
является первообразной функции  на бесконечной полупрямой
на бесконечной полупрямой 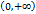 , так как
, так как  в каждой точке полупрямой
в каждой точке полупрямой 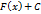 , где
, где 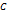 – произвольная постоянная, также является первообразной функции
– произвольная постоянная, также является первообразной функции 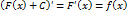 .
.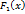 и
и 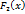 – любые две первообразные функции
– любые две первообразные функции 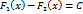 , где
, где 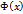 разность функций
разность функций  . Тогда в каждой точке интервала
. Тогда в каждой точке интервала 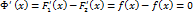 . Из теоремы 1.4 §1 главы 7 следует, что
. Из теоремы 1.4 §1 главы 7 следует, что  . Теорема 1.1 доказана.
. Теорема 1.1 доказана.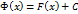 , где
, где 
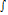 называется знаком интеграла, выражение
называется знаком интеграла, выражение  - подынтегральным выражением, а сама функция
- подынтегральным выражением, а сама функция  – переменной интегрирования.
– переменной интегрирования.
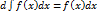 . Действительно, если
. Действительно, если 
 . Действительно,
. Действительно, 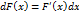 . Тогда
. Тогда  . Т.к.
. Т.к. 
 .
. – первообразная функции
– первообразная функции  , т.к.
, т.к.  . Из чего следует, что
. Из чего следует, что 
 , где
, где  .
.
 первообразные функций
первообразные функций 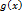 соответственно:
соответственно:
 , то функция
, то функция 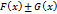 является первообразной функции
является первообразной функции  .
.


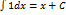




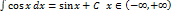




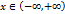

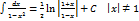
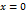 . Действительно, если
. Действительно, если 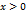 то из равенства
то из равенства  , а если
, а если  , то из равенства
, то из равенства  , заключаем, что
, заключаем, что 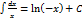 . Следовательно, формула 4 справедлива для любого
. Следовательно, формула 4 справедлива для любого  .
. . Тогда
. Тогда
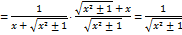
 . Поэтому
. Поэтому


 . Данная функция определена на множестве
. Данная функция определена на множестве  . Если
. Если  то
то 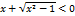 , поэтому для любой точки полупрямой
, поэтому для любой точки полупрямой 

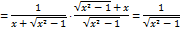

 , то
, то  , поэтому
, поэтому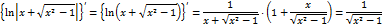
 .
.


