
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые и бесконечно большие функции.
Функция
Приведем эквивалентное определение бесконечно малой функции «на языке Функция Теорема 4.4. Сумма и произведение двух бесконечно малых, при
Следствие. Сумма и произведение конечного числа бесконечно малых, при Справедливость приведённого следствия непосредственно вытекает из теоремы 3.4. Функция
Функция Функция Из сказанного выше следует, что функция ограничена на отрезке
Теорема 4.5. Произведение ограниченной функции на бесконечно малую функцию является бесконечно малой функцией. Доказательство. Пусть Функция В этом случае пишут Если для любого
Если для любого Обозначение По аналогии определяются бесконечные левые пределы Теорема 4.6. Если функция Доказательство. Пусть Замечательные пределы. Первый замечательный предел. Докажем, что Этот предел принято называть первым замечательным пределом. Рассмотрим дугу единичной окружности, с центральным углом, радиальная мера которого равна
Тогда
Для завершения доказательства равенства (7), достаточно воспользоваться неравенствами (12) и теоремой 4.3. Второй замечательный предел. Доказательство равенства (13) основано на, доказанное в §4 равенство,
Третий замечательный предел. Докажем, что Действительно. Четвёртый замечательный предел. Докажем, что Очевидно, при
Пятый замечательный предел. Докажем, что Пользуясь основным логарифмическим тождеством, представим
Из равенства (14) имеем
Непрерывные функции. 1. Определение непрерывной функции по Гейне и по Коши. Пусть функция Функция Пользуясь определением предела функции по Гейне и по Коши, приведем следующие два определения непрерывной функции. Определение непрерывной функции по Гейне. Функция Определение непрерывной функции по Коши. Функция Очевидно, приведенные определения эквивалентны.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.181.231 (0.015 с.) |
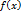 называется бесконечно малой функцией в точке
называется бесконечно малой функцией в точке  , если
, если 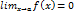 . Аналогично определяются бесконечно малые функции при
. Аналогично определяются бесконечно малые функции при 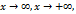
 .
. ».
». , существует такое положительное число
, существует такое положительное число  , что как только
, что как только  будет выполняться неравенство
будет выполняться неравенство 
 функций, являются бесконечно малыми функциями.
функций, являются бесконечно малыми функциями.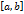 , если существует такое положительное число
, если существует такое положительное число  , что для всех
, что для всех 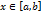 справедливо неравенство
справедливо неравенство 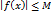 , или
, или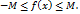 Ограниченность функции
Ограниченность функции 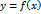 означает, что график этой функциивыходит из полосы
означает, что график этой функциивыходит из полосы 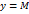 и
и 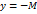 .
.
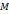 , что
, что 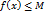 для каждого
для каждого 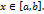
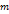 , что справедливо неравенство
, что справедливо неравенство  , для каждого
, для каждого 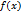 – ограниченная функция, а
– ограниченная функция, а 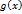 - бесконечно малая при
- бесконечно малая при 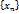 , сходящуюся к
, сходящуюся к 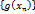 является бесконечно малой последовательностью, а
является бесконечно малой последовательностью, а 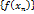 - ограниченной последовательностью. В силу теоремы 3.2 последовательность
- ограниченной последовательностью. В силу теоремы 3.2 последовательность 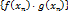 будет бесконечно малой, т.е.
будет бесконечно малой, т.е.  . Из последнего равенства следует утверждение теоремы.
. Из последнего равенства следует утверждение теоремы. (или при
(или при 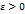 существует
существует 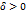 такое, что для всех
такое, что для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 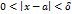 , справедливо неравенство
, справедливо неравенство  .
. и говорят, что функция стремится к бесконечности при
и говорят, что функция стремится к бесконечности при 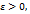 существует число
существует число 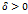 такое, что для всех
такое, что для всех  , то будем говорить, что функция
, то будем говорить, что функция  .
. справедливо неравенство
справедливо неравенство  .
.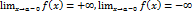 .
.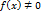 в некоторой окрестности точки
в некоторой окрестности точки 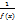 является бесконечно большой функцией в точке
является бесконечно большой функцией в точке  . Для этого числа существует положительное
. Для этого числа существует положительное 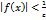 или
или  Следовательно, для всех
Следовательно, для всех  . Это означает, что
. Это означает, что 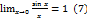 .
. .
.
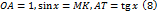 . Очевидно, что площадь
. Очевидно, что площадь 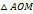 меньше площади сектора
меньше площади сектора  , которая меньше площади
, которая меньше площади 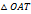 . Так как,
. Так как,  ,
, 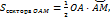
 , то
, то 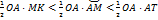 . Из этих неравенств и равенства (8), найдём:
. Из этих неравенств и равенства (8), найдём: 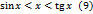 . Разделив обе части неравенств (9) на
. Разделив обе части неравенств (9) на 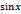 , найдём
, найдём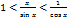 или
или 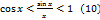 . Из неравенств (10) находим
. Из неравенств (10) находим  или
или  . Так как,
. Так как,  , то при
, то при  , справедливо неравенство
, справедливо неравенство  , поэтому из неравенств (11) имеем
, поэтому из неравенств (11) имеем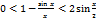 . Т.к.
. Т.к.  , то
, то 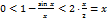 , т.е.
, т.е.  .
.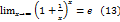 .
.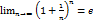 . Подробное доказательство равенства (13) см. Шипачёв В.С. «Высшая математика» стр. 81.
. Подробное доказательство равенства (13) см. Шипачёв В.С. «Высшая математика» стр. 81. .
.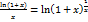 . Пусть
. Пусть 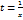 . Тогда
. Тогда  при
при 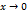 . Поэтому
. Поэтому 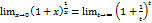 . В силу равенства (13), последний предел равен
. В силу равенства (13), последний предел равен 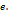 Тогда
Тогда 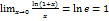 .
. .
. , равенство (14) выполнено. Пусть
, равенство (14) выполнено. Пусть 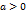 и
и  . Обозначим
. Обозначим 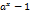 через
через  . Тогда
. Тогда 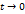 при
при  . Тогда
. Тогда 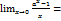
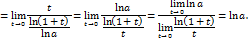
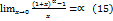 .
.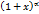 в виде
в виде 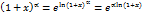 . Обозначим
. Обозначим 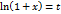 . Тогда
. Тогда 
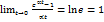 и
и  . Т.е.
. Т.е. 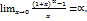
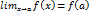 .
.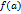 .
. такое, что для всех
такое, что для всех 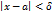 , справедливо неравенство
, справедливо неравенство  .
.


