Последовательность 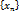 называется возрастающей, если
называется возрастающей, если 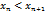 для всех
для всех  ; неубывающей, если
; неубывающей, если  для всех
для всех  ; убывающей, если
; убывающей, если  для всех
для всех  ; невозрастающей, если
; невозрастающей, если  для всех
для всех 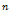 .
.
Все такие последовательности объединяются общим названием: монотонные последовательности. Возрастающие и убывающие последовательности называются также строго монотонными.
Теорема 3.10. Монотонная ограниченная последовательность сходится.
Рассмотрим случай неубывающей последовательности. Пусть  для всех
для всех  . Т.к. последовательность ограничена, то существует такое число
. Т.к. последовательность ограничена, то существует такое число 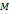 , что для всех номеров
, что для всех номеров  справедливо неравенство
справедливо неравенство 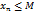 . Пусть
. Пусть 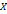 - множество, состоящее из элементов последовательности
- множество, состоящее из элементов последовательности 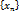 , т.е.
, т.е.
 . Тогда
. Тогда 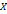 - непустое, ограниченное сверху множество. Поэтому по теореме 2.1 для множества
- непустое, ограниченное сверху множество. Поэтому по теореме 2.1 для множества 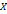 существует точная верхняя грань
существует точная верхняя грань  , т.е.
, т.е.  . Докажем, что
. Докажем, что  является пределом последовательности
является пределом последовательности 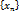 .
.
Т.к.  - точная верхняя грань множества
- точная верхняя грань множества  , то для любого
, то для любого 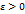 существует такой элемент
существует такой элемент 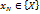 , что
, что  . С другой стороны, по определению точной верхней грани
. С другой стороны, по определению точной верхней грани  для всех
для всех  . Из неравенств (22), (23) и из условия неубывания последовательности
. Из неравенств (22), (23) и из условия неубывания последовательности 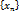 найдём
найдём
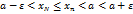 для всех
для всех 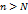 .
.
Из последних неравенств имеем
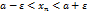 для всех
для всех 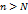 или
или
 для всех
для всех 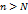 .
.
Т.е.  является пределом последовательности
является пределом последовательности 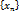 .
.
Отметим, что аналогично рассматривается случай невозрастающей ограниченной последовательности с той лишь разницей, что вместо  надо рассмотреть
надо рассмотреть  . Теорема доказана.
. Теорема доказана.
4. Число  . Рассмотрим последовательность
. Рассмотрим последовательность 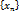 с общим членом
с общим членом  . Докажем, что последовательность
. Докажем, что последовательность 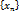 является возрастающей и ограниченной сверху. Тогда из теоремы 3.10 будет следовать существование предела этой последовательности.
является возрастающей и ограниченной сверху. Тогда из теоремы 3.10 будет следовать существование предела этой последовательности.
Воспользуемся формулой бинома Ньютона.
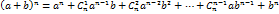 ,
,
где  – число сочетаний из
– число сочетаний из  элементов по
элементов по 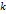 элементов и
элементов и  , где
, где  .
.
Тогда 


Подставляя в это равенство в место индекса 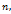
 , найдем
, найдем

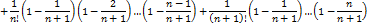
Так как для любого натурального 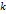
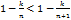 , то каждое слагаемое в выражении для
, то каждое слагаемое в выражении для 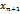 , начиная со второго слагаемого, больше, чем соответствующее слагаемое в выражении для
, начиная со второго слагаемого, больше, чем соответствующее слагаемое в выражении для 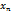 , кроме этого
, кроме этого 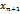 содержит на одно положительное слагаемое больше, чем
содержит на одно положительное слагаемое больше, чем 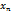 , т.е.
, т.е.  . Тем самым, монотонное возрастание последовательности
. Тем самым, монотонное возрастание последовательности 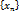 доказано. Докажем ограниченность последовательности
доказано. Докажем ограниченность последовательности 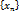 .
.
Для доказательства ограниченности сверху этой последовательности заметим, что для любого  справедливо неравенство
справедливо неравенство  . Поэтому
. Поэтому

Т.е.  для всех
для всех  . Т.е. последовательность
. Т.е. последовательность 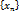 ограничена сверху.
ограничена сверху.
Итак, последовательность 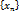 является монотонно возрастающей ограниченной сверху последовательностью. По теореме 3.10 она сходится к некоторому пределу, который мы обозначим через
является монотонно возрастающей ограниченной сверху последовательностью. По теореме 3.10 она сходится к некоторому пределу, который мы обозначим через 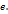
Итак,  (24)
(24)
Отметим, что число  является иррациональным (без доказательства) числом, имеющим с точностью до пятнадцати знаков после запятой вид
является иррациональным (без доказательства) числом, имеющим с точностью до пятнадцати знаков после запятой вид
Функция и её предел.
1. Понятие функции. Пусть 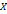 и
и 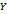 - непустые числовые множества. Если каждому элементу
- непустые числовые множества. Если каждому элементу  по некоторому закону
по некоторому закону 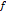 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  , то говорят, что на множестве
, то говорят, что на множестве 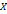 задана функция
задана функция 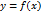 , при этом переменная
, при этом переменная  называется аргументом или независимой переменной, множество
называется аргументом или независимой переменной, множество 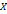 называется областью определения функции. Совокупность всех значений
называется областью определения функции. Совокупность всех значений 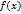 называется областью изменения функции.
называется областью изменения функции.
Примеры функций.
1.  . Эта функция определена на всей числовой прямой
. Эта функция определена на всей числовой прямой  . Областью изменения является полупрямая
. Областью изменения является полупрямая  .
.
2. 
Областью определения является множество  . Область изменения состоит из двух точек: 0 и 1.
. Область изменения состоит из двух точек: 0 и 1.
3. 
2. Предел функции по Гейне и по Коши. Пусть  – бесконечное числовое множество.
– бесконечное числовое множество.
Точка  бесконечной прямой
бесконечной прямой  называется предельной точкой множества
называется предельной точкой множества  , если в любой
, если в любой  окрестности точки
окрестности точки  (т.е. в любом интервале
(т.е. в любом интервале 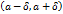 ) имеются точки множества
) имеются точки множества  , отличные от точки
, отличные от точки  .
.
Замечание. Точка  может, как принадлежать множеству
может, как принадлежать множеству  , так и не принадлежать ему.
, так и не принадлежать ему.
Например, для интервала 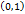 очевидно,
очевидно,  является предельной точкой. Однако
является предельной точкой. Однако 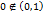 . Для сегмента
. Для сегмента  точка
точка  является предельной точкой. В последнем случае
является предельной точкой. В последнем случае  .
.
Пусть функция 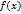 определена на множестве
определена на множестве  и точка
и точка  предельная точкой этого множества.
предельная точкой этого множества.
Предел функции по Гейне. Число  называется пределом функции
называется пределом функции 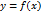 в точке
в точке  , если для любой последовательности значений аргументов
, если для любой последовательности значений аргументов 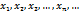 , сходящейся к
, сходящейся к  , элементы которой отличны от
, элементы которой отличны от  соответствующая последовательность
соответствующая последовательность  сходится к числу
сходится к числу  .
.
Предел функции по Коши. Число  называется пределом функции в точке
называется пределом функции в точке  , если для любого положительного числа
, если для любого положительного числа  найдётся положительное число
найдётся положительное число  , такое, что для всех значений аргумента
, такое, что для всех значений аргумента  , удовлетворяющих условию
, удовлетворяющих условию 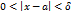 справедливо неравенство
справедливо неравенство

Замечание. Отметим, что в определении предела функции по Гейне говорится, что элементы 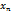 отличны от
отличны от  , а в определении предела по Коши, что
, а в определении предела по Коши, что 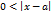 . Эти требования вызваны тем, что функция
. Эти требования вызваны тем, что функция  может быть не определена в точке
может быть не определена в точке  .
.
Докажем теперь эквивалентность приведенных определений.
Пусть  является пределом функции
является пределом функции  по Коши. Возьмём произвольную последовательность элементов
по Коши. Возьмём произвольную последовательность элементов 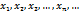 , отличных от
, отличных от  и сходящихся к
и сходящихся к  . Тогда для произвольного
. Тогда для произвольного 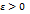 найдется такое положительное число
найдется такое положительное число 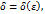 что при всех значениях аргумента
что при всех значениях аргумента  для которых выполнено неравенство
для которых выполнено неравенство  будет выполнено
будет выполнено 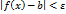 . Так как последовательность
. Так как последовательность 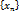 сходится к
сходится к  , то для числа
, то для числа  существует такой номер
существует такой номер  , что для всех номеров
, что для всех номеров 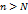 справедливо неравенство
справедливо неравенство  . Но для таких аргументов
. Но для таких аргументов 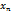 справедливо неравенство
справедливо неравенство
 .
.
Итак, для любого 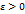 существует такой номер
существует такой номер 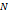 , что для всех номеров
, что для всех номеров 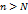 , выполняется
, выполняется

Следовательно, число  является пределом последовательности
является пределом последовательности  .
.
Таким образом, если  является пределом функции
является пределом функции  в точке
в точке  по Коши, то
по Коши, то  является пределом функции
является пределом функции  и по Гейне.
и по Гейне.
Докажем теперь обратное. Пусть  - предел функции по Гейне. Предположим, что
- предел функции по Гейне. Предположим, что  не является пределом функции
не является пределом функции  по Коши. Тогда должно существовать такое положительное число
по Коши. Тогда должно существовать такое положительное число 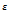 , что для произвольного положительного числа
, что для произвольного положительного числа  , найдется, хотя бы одно значение аргумента
, найдется, хотя бы одно значение аргумента  , для которого
, для которого 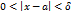 , но
, но 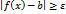 .
.
Возьмём последовательность  , где
, где  . Для каждого
. Для каждого  должен существовать такой элемент
должен существовать такой элемент 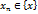 , для которого выполнены неравенства:
, для которого выполнены неравенства: 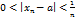 (2) и
(2) и 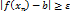 . (3).
. (3).
Из неравенства (2) следует, что последовательность 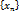 сходится к
сходится к  и состоит из чисел, отличных от
и состоит из чисел, отличных от  . Тогда по условию последовательность
. Тогда по условию последовательность 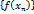 сходится к числу
сходится к числу  . В тоже время, из неравенства (3) следует, что последовательность
. В тоже время, из неравенства (3) следует, что последовательность 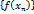 не сходится к
не сходится к  . Т.е. получаем противоречие, что вызвано предположением о том, что число
. Т.е. получаем противоречие, что вызвано предположением о том, что число  не является пределом функции по Коши. Итак, эквивалентность приведенных определений доказана.
не является пределом функции по Коши. Итак, эквивалентность приведенных определений доказана.
3. Односторонние пределы.
Определение одностороннего предела по Гейне. Число  называется правым (левым) пределом функции
называется правым (левым) пределом функции  в точке
в точке  , если для любой сходящейся к
, если для любой сходящейся к  последовательности
последовательности 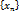 , элементы
, элементы 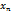 которой больше (меньше)
которой больше (меньше)  , соответствующая последовательность
, соответствующая последовательность 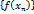 сходится к числу
сходится к числу  .
.
Обозначение 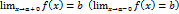 .
.
Определение одностороннего предела по Коши. Число  называется правым (левым) пределом функции
называется правым (левым) пределом функции  в точке
в точке  , если для любого
, если для любого 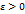 существует
существует 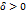 такое, что для всех
такое, что для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  выполняется неравенство
выполняется неравенство 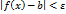 .
.
Повторяя рассуждения, приведенные в п.2, без особого труда, можно доказать эквивалентность приведенных определений.
Рассмотрим в качестве примера функцию  . Для этой функции имеем
. Для этой функции имеем
 р
р
так как, для любой сходящейся к  последовательности
последовательности 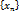 , элементы которой больше
, элементы которой больше  имеем
имеем  , а для любой сходящейся к
, а для любой сходящейся к  последовательности
последовательности 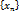 , элементы которой меньше
, элементы которой меньше 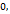
 поэтому
поэтому  ,
,  .
.
Теорема 4.1. Функция  имеет в точке
имеет в точке  предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам.
предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам.
Доказательство. Пусть  . Тогда, согласно определению предела функции слева и справа, для любого
. Тогда, согласно определению предела функции слева и справа, для любого 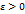 существуют числа
существуют числа  и
и  , такие, что для всех
, такие, что для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  и для всех
и для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  справедливо неравенство
справедливо неравенство  .
.
Пусть  , тогда для всех
, тогда для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 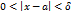 будет выполнено хотя бы одно из двух неравенств (4) и (5), но при таких значениях
будет выполнено хотя бы одно из двух неравенств (4) и (5), но при таких значениях  верно неравенство (6). Итак, для любого положительного
верно неравенство (6). Итак, для любого положительного  существует такое положительное число
существует такое положительное число  , что для всех
, что для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 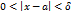 , выполнено неравенство
, выполнено неравенство 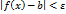 . Т.е.
. Т.е.  является пределом функции
является пределом функции  в точке
в точке  .
.
Обратно. Пусть  . Тогда для любого
. Тогда для любого 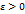 , существует
, существует 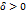 такое, что как только
такое, что как только 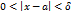 , справедливо неравенство
, справедливо неравенство 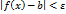 . Следовательно, неравенство
. Следовательно, неравенство 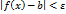 верно для всех
верно для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 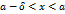 и для всех
и для всех  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  . Но в таком случае, из определения левого и правого пределов следует, что
. Но в таком случае, из определения левого и правого пределов следует, что  и
и 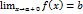 . Теорема 4.1 доказана.
. Теорема 4.1 доказана.
4. Предел функции при 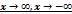 и при
и при 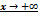 .
.
Предел функции при 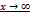 по Гейне. Число
по Гейне. Число  называется пределом функции
называется пределом функции  при
при 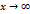 , если для любой бесконечно большой последовательности значений аргумента
, если для любой бесконечно большой последовательности значений аргумента 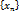 , соответствующая последовательность значений функции
, соответствующая последовательность значений функции 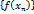 сходится к числу
сходится к числу  .
.
Предел функции при 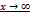 по Коши. Число
по Коши. Число  называется пределом функции
называется пределом функции  при
при 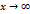 , если для любого положительного числа
, если для любого положительного числа  найдётся отвечающее ему положительное число
найдётся отвечающее ему положительное число  такое, что для всех
такое, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 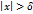 , справедливо неравенство
, справедливо неравенство 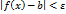 .
.
Предел функции  при
при  (при
(при 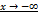 ) по Гейне. Число
) по Гейне. Число  называется пределом функции
называется пределом функции  при
при  (
(  ), если для любой бесконечно большой последовательности значений аргумента
), если для любой бесконечно большой последовательности значений аргумента 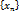 , все элементы которой положительны (отрицательны), соответствующая последовательность
, все элементы которой положительны (отрицательны), соответствующая последовательность 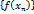 сходится к числу
сходится к числу  .
.
Предел функции  по Коши. Число
по Коши. Число  называется пределом функции
называется пределом функции  при
при  (
(  ), если для любого
), если для любого  существует число
существует число  такое, что для всех значений аргумента
такое, что для всех значений аргумента  , удовлетворяющих неравенству
, удовлетворяющих неравенству 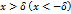 , справедливо неравенство
, справедливо неравенство
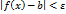 .
.
Для обозначения введённых выше пределов используется следующая символика: 
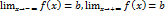 .
.


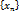 называется возрастающей, если
называется возрастающей, если 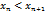 для всех
для всех  ; неубывающей, если
; неубывающей, если  для всех
для всех  для всех
для всех  для всех
для всех 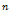 .
.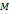 , что для всех номеров
, что для всех номеров 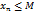 . Пусть
. Пусть 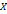 - множество, состоящее из элементов последовательности
- множество, состоящее из элементов последовательности  . Тогда
. Тогда  , т.е.
, т.е.  . Докажем, что
. Докажем, что  , то для любого
, то для любого 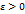 существует такой элемент
существует такой элемент 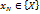 , что
, что  . С другой стороны, по определению точной верхней грани
. С другой стороны, по определению точной верхней грани  для всех
для всех 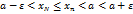 для всех
для всех 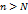 .
.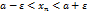 для всех
для всех  для всех
для всех  надо рассмотреть
надо рассмотреть  . Теорема доказана.
. Теорема доказана. . Рассмотрим последовательность
. Рассмотрим последовательность  . Докажем, что последовательность
. Докажем, что последовательность 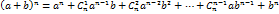 ,
, – число сочетаний из
– число сочетаний из 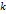 элементов и
элементов и  , где
, где  .
.


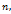
 , найдем
, найдем
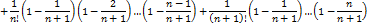
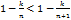 , то каждое слагаемое в выражении для
, то каждое слагаемое в выражении для 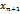 , начиная со второго слагаемого, больше, чем соответствующее слагаемое в выражении для
, начиная со второго слагаемого, больше, чем соответствующее слагаемое в выражении для 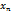 , кроме этого
, кроме этого  . Тем самым, монотонное возрастание последовательности
. Тем самым, монотонное возрастание последовательности  справедливо неравенство
справедливо неравенство  . Поэтому
. Поэтому
 для всех
для всех 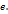
 (24)
(24) является иррациональным (без доказательства) числом, имеющим с точностью до пятнадцати знаков после запятой вид
является иррациональным (без доказательства) числом, имеющим с точностью до пятнадцати знаков после запятой вид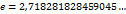
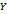 - непустые числовые множества. Если каждому элементу
- непустые числовые множества. Если каждому элементу  по некоторому закону
по некоторому закону 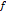 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  , то говорят, что на множестве
, то говорят, что на множестве 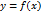 , при этом переменная
, при этом переменная 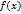 называется областью изменения функции.
называется областью изменения функции. . Эта функция определена на всей числовой прямой
. Эта функция определена на всей числовой прямой  . Областью изменения является полупрямая
. Областью изменения является полупрямая  .
.

 – бесконечное числовое множество.
– бесконечное числовое множество. окрестности точки
окрестности точки 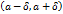 ) имеются точки множества
) имеются точки множества 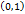 очевидно,
очевидно,  является предельной точкой. Однако
является предельной точкой. Однако 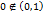 . Для сегмента
. Для сегмента  точка
точка  .
. называется пределом функции
называется пределом функции 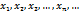 , сходящейся к
, сходящейся к  соответствующая последовательность
соответствующая последовательность  сходится к числу
сходится к числу  найдётся положительное число
найдётся положительное число  , такое, что для всех значений аргумента
, такое, что для всех значений аргумента  , удовлетворяющих условию
, удовлетворяющих условию 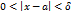 справедливо неравенство
справедливо неравенство 
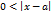 . Эти требования вызваны тем, что функция
. Эти требования вызваны тем, что функция  может быть не определена в точке
может быть не определена в точке 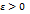 найдется такое положительное число
найдется такое положительное число 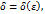 что при всех значениях аргумента
что при всех значениях аргумента  будет выполнено
будет выполнено 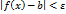 . Так как последовательность
. Так как последовательность  существует такой номер
существует такой номер  , что для всех номеров
, что для всех номеров  . Но для таких аргументов
. Но для таких аргументов  .
.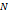 , что для всех номеров
, что для всех номеров 
 является пределом последовательности
является пределом последовательности  .
.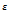 , что для произвольного положительного числа
, что для произвольного положительного числа 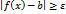 .
. , где
, где  . Для каждого
. Для каждого  должен существовать такой элемент
должен существовать такой элемент 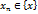 , для которого выполнены неравенства:
, для которого выполнены неравенства: 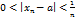 (2) и
(2) и 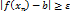 . (3).
. (3).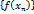 сходится к числу
сходится к числу 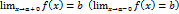 .
.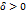 такое, что для всех
такое, что для всех  выполняется неравенство
выполняется неравенство  . Для этой функции имеем
. Для этой функции имеем р
р имеем
имеем  , а для любой сходящейся к
, а для любой сходящейся к 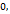
 поэтому
поэтому  ,
,  .
. . Тогда, согласно определению предела функции слева и справа, для любого
. Тогда, согласно определению предела функции слева и справа, для любого  и
и  , такие, что для всех
, такие, что для всех  и для всех
и для всех  справедливо неравенство
справедливо неравенство  .
. , тогда для всех
, тогда для всех  . Тогда для любого
. Тогда для любого 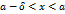 и для всех
и для всех  . Но в таком случае, из определения левого и правого пределов следует, что
. Но в таком случае, из определения левого и правого пределов следует, что  и
и 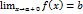 . Теорема 4.1 доказана.
. Теорема 4.1 доказана.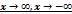 и при
и при 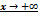 .
.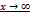 по Гейне. Число
по Гейне. Число 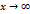 , если для любой бесконечно большой последовательности значений аргумента
, если для любой бесконечно большой последовательности значений аргумента 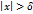 , справедливо неравенство
, справедливо неравенство  при
при  (при
(при 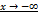 ) по Гейне. Число
) по Гейне. Число  (
(  ), если для любой бесконечно большой последовательности значений аргумента
), если для любой бесконечно большой последовательности значений аргумента  по Коши. Число
по Коши. Число  существует число
существует число  такое, что для всех значений аргумента
такое, что для всех значений аргумента 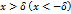 , справедливо неравенство
, справедливо неравенство
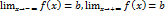 .
.


