
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операция сложения и умножения вещественных чисел.
Справедливо следующее утверждение: Теорема 2.2. Для произвольного натурального Доказательство. Приведём доказательство для случая неотрицательного числа Из правил сравнения вещественных чисел следует, что Случай неположительного Приведенная теорема имеет важное практическое значение, так как любое вещественное число можно заменить рациональным числом с требуемой степенью точности. Важнейшим вопросом теории вещественных чисел является вопрос об определении операций сложения и умножения действительных чисел и о свойствах этих операций. Начнём с определения операции сложения вещественных чисел. Известно как на практике складывают два вещественных числа Приведенное выше практическое правило лежит в основе определения суммы двух вещественных чисел. Суммой вещественных чисел
для любых рациональных чисел
Оказывается, что такое вещественное число Аналогичным образом вводится понятие произведения двух положительных вещественных чисел. Произведением положительных вещественных чисел
Точно так же, как и для суммы, такое число
Произведение вещественных чисел произвольного знака определяется следующим образом: 1) считают, что 2) считают, что Введём теперь понятие разности и частного двух действительных чисел. Разностью действительных чисел
Частным двух вещественных чисел Итак, для действительных чисел мы ввели правило сравнения и операции сложения и умножения. Оказывается, для множества действительных чисел переносятся все 13 основных свойство сформулированных в пункте 1 параграфа 1. В заключение отметим, что множество действительных чисел уже нельзя расширить до более широкого множества, в котором остались бы справедливыми правила сравнения, сложения, умножения и 13 основных свойств, т.е. множество вещественных чисел является полным относительно трёх указанных правил и 13 основных свойств.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.36.192 (0.005 с.) |
 и произвольного действительного числа
и произвольного действительного числа  найдутся два рациональных числа
найдутся два рациональных числа  и
и 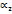 , такие, что
, такие, что  и
и  .
. . Фиксируем номер
. Фиксируем номер 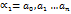 . Прибавив к рациональному числу
. Прибавив к рациональному числу  , мы получим другое рациональное число
, мы получим другое рациональное число 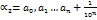 . Очевидно, что
. Очевидно, что 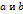 : их заменяют с требуемой степенью точности рациональными числами
: их заменяют с требуемой степенью точности рациональными числами 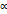 и
и  и за приближённое значение их суммы
и за приближённое значение их суммы  берут сумму указанных рациональных чисел. При этом предполагается, что чем точнее рациональные числа
берут сумму указанных рациональных чисел. При этом предполагается, что чем точнее рациональные числа  приближает то вещественное число, которое должно являться суммой вещественных чисел
приближает то вещественное число, которое должно являться суммой вещественных чисел  и
и  называется такое вещественное число
называется такое вещественное число  , которое удовлетворяет неравенствам
, которое удовлетворяет неравенствам
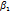 ,
, 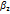 удовлетворяющих неравенствам
удовлетворяющих неравенствам .
.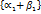 сумм всех рациональных чисел
сумм всех рациональных чисел  и
и  .
.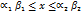 , где
, где 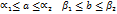
 , где
, где 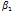 - произвольные положительные рациональные числа, удовлетворяющие неравенствам
- произвольные положительные рациональные числа, удовлетворяющие неравенствам 


 , что
, что  . Разность чисел
. Разность чисел  .
.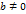 называется такое вещественное число
называется такое вещественное число  .
.


