
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каноническое уравнение прямой в плоскости.
Пусть Запишем параметрические уравнения прямой.
Определяя из каждого уравнения параметр
Уравнение (3) называется каноническим уравнением прямой. Из приведённых выше рассуждений следует, что точка Если
Рассмотрим прямоугольную декартову систему координат Справедлива следующая теорема. Теорема 2.1. Если прямая
где хотя бы один из коэффициентов Уравнение (4) называется общим уравнением прямой на плоскости. Доказательство. Пусть
Умножая первое уравнение на Обозначая Следовательно, уравнение прямой Докажем теперь обратное. Пусть дано уравнение (4). Ниже мы покажем, что существует некоторая прямая Рассмотрим систему уравнений, состоящую из одного уравнения
По условию
Вычитая из второго тождества первое, получим
Рассмотрим два вектора Из равенства (9), в частности следует, что векторы Рассмотрим в плоскости
Пусть Т.к.
Из первого равенства равенств (7) следует, что Следовательно, координаты точек прямой Любой ненулевой вектор, ортогональный к заданной прямой, называется нормальным вектором этой прямой. Замечание. Из доказательства теоремы 2.1 следует, что вектор
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.22.136 (0.006 с.) |
 - произвольная прямая в плоскости
- произвольная прямая в плоскости 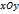 .
. 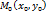 - произвольная точка этой прямой.
- произвольная точка этой прямой. 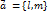 – направляющий вектор прямой
– направляющий вектор прямой 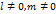 .
.
 , а затем приравнивая полученные значения, получим
, а затем приравнивая полученные значения, получим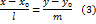
 лежит на прямой
лежит на прямой 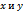 удовлетворяют уравнению (3).
удовлетворяют уравнению (3). , то из параметрического уравнения (2) имеем
, то из параметрического уравнения (2) имеем  . Если
. Если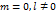 то
то  .
. 3. Общее уравнение прямой в плоскости.
3. Общее уравнение прямой в плоскости.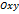 .
.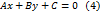
 отличен от нуля. И наоборот. Всякое уравнение (1), в котором хотя бы один из коэффициентов
отличен от нуля. И наоборот. Всякое уравнение (1), в котором хотя бы один из коэффициентов  определяет прямую.
определяет прямую.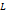 – произвольная прямая плоскости
– произвольная прямая плоскости 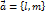 – её направляющий вектор,
– её направляющий вектор, 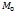 – произвольная точка прямой
– произвольная точка прямой 
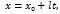
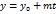 .
.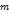 , а второе на
, а второе на 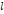 , а затем вычитая из первого равенства второе, получим
, а затем вычитая из первого равенства второе, получим  или
или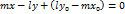 . (5)
. (5) , запишем уравнение (5) в виде
, запишем уравнение (5) в виде
 вектор
вектор 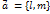 является направляющим вектором прямой
является направляющим вектором прямой  не могут одновременно равняться нулю, следовательно, хотя бы один из коэффициентов
не могут одновременно равняться нулю, следовательно, хотя бы один из коэффициентов  отличен от нуля.
отличен от нуля. (6)
(6)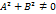 , по этому, система из одного уравнения с неизвестными
, по этому, система из одного уравнения с неизвестными 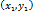 и
и  - два различных решения уравнения (3). Т.е.
- два различных решения уравнения (3). Т.е.

 и
и 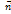 , где
, где 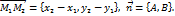 Тогда равенство (8) можно записать в виде
Тогда равенство (8) можно записать в виде . (9)
. (9)  и
и 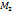
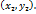 Покажем, что координаты любой точки прямой, проходящей через точки
Покажем, что координаты любой точки прямой, проходящей через точки  и только они удовлетворяют уравнению (4).
и только они удовлетворяют уравнению (4). 
 - произвольная точка плоскости. Очевидно, что точка
- произвольная точка плоскости. Очевидно, что точка  тогда и только тогда, когда вектор
тогда и только тогда, когда вектор 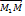 коллинеарен вектору
коллинеарен вектору  . Следовательно точка
. Следовательно точка  . (10)
. (10)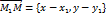 ,
, 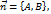 то равенство (10) можно записать в виде:
то равенство (10) можно записать в виде: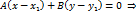
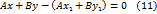
 . Учитывая это в равенстве (11), получим
. Учитывая это в равенстве (11), получим  .
.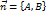 является одним из нормальных векторов прямой, определяемой уравнением
является одним из нормальных векторов прямой, определяемой уравнением 


