
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы с квадратной невырожденной матрицей.
Рассмотрим системы линейных алгебраических уравнений, состоящей из
Пусть Запишем систему (1) в матричной форме
Теорема 2.1. Система линейных алгебраических уравнений с квадратной невырожденной матрицей совместна и имеет единственное решение. Доказательство. Основная матрица системы (1) не вырождена, следовательно она обратима, т.е. для неё существует обратная матрица Умножая обе части равенства
Равенство (3) определяет решение матричного уравнения (2). Матрица Докажем теперь, что найденное решение Пусть
Умножая обе части равенства (4) слева на матрицу Сопоставляя равенства (3) и (5), приходим к выводу Правило Крамера. При доказательстве теоремы 2.1 была получена матричная форма записи решения системы (1).
получим
Следовательно
Введём следующие обозначения
Заметим, что определители Раскладывая определитель
Учитывая равенства (7) в равенствах (6) мы получим
Формулы (8) называются формулами Крамера. Пример. Пользуясь формулами Крамера, решить систему: Вычислим определитель основной матрицы системы:
Вычислим определители
Следовательно
§3. Элементарные преобразования системы линейных алгебраических уравнений. Понятие эквивалентной системы. Рассмотрим две системы линейных алгебраических уравнений с одинаковым количеством неизвестных
Заметим, что числа
Системы (1) и (2) с одинаковым количеством неизвестных называются эквивалентными, если каждое решение системы (1) является решением системы (2) и наоборот – каждое решение системы (2) является решением системы (1). Элементарные преобразования системы. Элементарными преобразованиями системы называются преобразования следующих трёх типов. 1. Перестановка местами любых двух уравнений системы; 2. Умножение любого уравнения системы на любое отличное от нуля число; 3. Прибавление к одному уравнению системы другого её уравнения, умноженного на любое число. Заметим, что элементарные преобразования системы означают элементарные преобразования сток её расширенной матрицы. Теорема 3.1. Элементарные преобразования системы линейных алгебраических уравнений приводят её к эквивалентной системе. Справедливость теоремы 3.1 непосредственно вытекает из определения эквивалентных систем.
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.226.105 (0.01 с.) |
 уравнений и
уравнений и 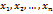 .
.
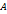 - основная матрица системы (1),
- основная матрица системы (1),  - столбец неизвестных и
- столбец неизвестных и  – столбец свободных членов.
– столбец свободных членов.
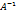 .
.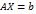 слева на матрицу
слева на матрицу 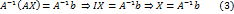
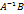 является матрицей столбцом размера
является матрицей столбцом размера 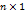 . Записывая равенство (3) в развёрнутом виде, т.е. приравнивая элементы в одинаковых позициях. Мы найдём значения
. Записывая равенство (3) в развёрнутом виде, т.е. приравнивая элементы в одинаковых позициях. Мы найдём значения  – любое решение системы (1). Тогда матрица столбец
– любое решение системы (1). Тогда матрица столбец  будет удовлетворять матричному равенству
будет удовлетворять матричному равенству
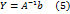 .
.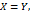 что доказывает единственность решения системы (1).
что доказывает единственность решения системы (1). . Учитывая, что
. Учитывая, что
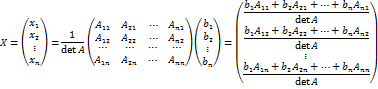

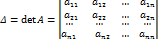

 отличаются от определителя
отличаются от определителя 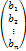 .
.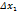 по первому столбцу, определитель
по первому столбцу, определитель 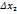 по второму столбцу и т.д. Определитель
по второму столбцу и т.д. Определитель  по последнему столбцу, получим
по последнему столбцу, получим

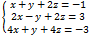



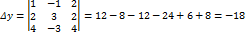

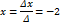

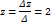


 могут не совпадать. Т.е. количество уравнений системы (1) может не совпадать с количеством уравнений системы (2).
могут не совпадать. Т.е. количество уравнений системы (1) может не совпадать с количеством уравнений системы (2).


