
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статические и динамические режимы и характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статические режимы СУИМ характеризуются установив- шимися состояниями при неизменных входных воздействиях. Уравнения статики легко получить из уравнений динамики СУИМ, приравняв в них к нулю все производные переменных (ко- ординат состояния) по времени и внешних воздействий. В опера- торных уравнениях и структурных схемах линейных САУ это эк- вивалентно приравниванию к нулю оператора p. Таким образом, статическая характеристика системы (элемента) – это зави- симость выходной переменной системы (элемента) от какой-либо входной переменной в установившемся режиме. Примером статической характеристики является механиче- ская характеристика электропривода – зависимость угловой часто- ты вращения вала двигателя от момента статической нагрузки на валу в установившихся режимах. Для электропривода постоянного тока такая характеристика приведена на рис. 2.3. Как видим, при увеличении нагрузки на валу двигателя ско- рость вращения вала двигателя падает и появляется статическая ошибка регулирования скорости. При изменении нагрузки от нуля до номинального значения M сн скорость вращения уменьшается от скорости холостого хода ω0 до номинальной скорости ωн. В номинальном режиме абсолютная величина статической ошибки регулирования скорости вращения Dwc = w0 - wн. Найдем выражения для установившейся ошибки регулирова- ния в общем случае изменения входного (задающего или возму- щающего) воздействия линейной СУИМ.
M 0 M сн
Рис. 2.3. Статическая механическая характеристика двигателя постоянного тока
Передаточная функция любого замкнутого контура регулиро- вания электропривода с отрицательной обратной связью (рис. 2.4) определяется передаточными функциями прямого W 1(p) и обрат- ного W 2(p) каналов регулирования [13, 14]:
W р W 1 (p).
з X (p) W 1 (p) W 2 (p) + 1 Отсюда изображение ошибки регулирования в системе e(p) = X (p) - W 1 (p) W 2 (p)e(p) = 1
(p) + 1 X (p), (2.1)
(2.2) X (p) W 1 (p) W 2 (p) + 1
Рис. 2.4. Структурная схема замкнутого контура регулирования
Как следует из формулы (2.1), ошибка регулирования будет стремиться к нулю при X = const, если W 1 (p) W 2 (p) ® ¥, что предполагает реализацию бесконечно большого усиления в уст- ройстве управления и может привести к неустойчивости системы. Кроме того, реальные динамические звенья обладают конечными коэффициентами усиления, что приводит к возникновению нену- левой статической ошибки регулирования. Такие системы приня- то называть статическими. Между тем статическая ошибка регулирования в системе при неизменном входном воздействии X может быть сведена к нулю, если сделать равной нулю передаточную функцию W e (p) при p = 0. Для этого достаточно в прямой или обратный канал регули- рования системы, приведенной на рис. 2.4, ввести интегрирующее звено. На практике интегрирующее звено вводят в структуру уст- ройства управления, применяя И-, ПИ-, ПИД-регуляторы. Это обеспечивает W 1 (p) ®¥ и тем самым нулевую статическую ошибку регулирования. Такие системы принято называть аста- тическими нулевого порядка по задающему или(и) возмущающе- му воздействию. Для придания системе астатизма более высокого (первого) порядка в структуру регулятора вводят два интегратора. Часто в структуре самого объекта управления имеются интегри- рующие звенья, например ГИМ, что заведомо придает системе свойство астатизма. Величина установившейся ошибки регулирования, наличие и порядок астатизма замкнутой САУ определяются не только ее моделью, но и видом входного сигнала. Определим, как вид вход- ного воздействия влияет на величину установившейся ошибки. Передаточную функцию разомкнутой СУИМ запишем в виде
K Õ(p + zi)
(2.3)
j =1 где K – коэффициент передачи; pj, zi – полюсы и нули передаточ- ной функции (2.3). В установившихся режимах (при p = 0) передаточную функ- цию (2.2) можно записать в виде
1,
где Ki – коэффициент ошибки системы, определяемый видом входного воздействия, i = 0, 1, 2. Поскольку в качестве типовых тестовых сигналов применяют ступенчатое (для систем стабилизации), линейное и квадратичное (для программных и следящих СУИМ) входные воздействия, для оценки установившихся ошибок в системе выделяют три типа ко- эффициентов ошибок: 1) коэффициент ошибки по положению (i = 0)
p 2) коэффициент ошибки по скорости (i = 1)
p 3) коэффициент ошибки по ускорению (i = 2) K = lim p 2 W (p). 2 p ®¥ раз Установившиеся ошибки для трех типов входных воздейст- вий и трех типов передаточной функции W раз(p) – с отсутствием интеграторов, с одним и двумя интеграторами – приведены в табл. 2.1. Таблица 2.1 Установившиеся ошибки регулирования СУИМ
Динамические режимы СУИМ характеризуются переход- ными состояниями системы при изменении начального состояния, а также входных (задающих и(или) возмущающих) воздействий. При этом различают свободные и вынужденные процессы. Свободный (собственный) процесс в системе определяется ре- шением однородного дифференциального уравнения, описывающе- го СУИМ, протекает под действием ненулевых начальных условий Y (t 0) ≠ 0 и в устойчивых системах асимптотически затухает:
(2.4)
где e A (t - t 0)
– матрица перехода системы из начального Y (t 0) в текущее Y (t) состояние. Назовем процесс вынужденным, если промежуток времени между моментом t з(t в) приложения задающего (возмущающего) воздействия X (t) и моментом наблюдения выходной величины Y (t) равен бесконечности. Тогда процесс изменения выходной величи- ны будет иметь вид [1, 16]
¥ Y (t ) = ò w (t) X (t - t) d t, 0
(2.5) где w (τ) – импульсная переходная функция по задающему (возму- щающему) воздействию. Полное решение уравнения движения линейных СУИМ пред- ставляет собой сумму решений уравнений свободного и вынуж- денного движения. В теории управления к типовым тестовым воздействиям от- носят, как правило, единичное ступенчатое и единичное импульс- ное воздействия. Соответствующие динамические реакции систем на эти воздействия называют переходным процессом и импульсным переходным процессом. В качестве примера на рис. 2.5 приведена реакция электро- двигателя постоянного тока на ступенчатое приложение номи- нальной нагрузки M сн к его валу (возмущающего воздействия). При приложении номинальной нагрузки скорость ω(t) двига- теля падает, причем имеет место колебательный процесс. Макси- мальный динамический провал скорости Δωдин может превышать статическое падение скорости Δωс (см. рис. 2.5). Вынужденное движение соответствует новому установивше- муся состоянию – номинальной скорости ωн электродвигателя. Время переходного процесса (перехода в новое установившееся состояние) составляет t рег. Задача исследования динамических свойств СУИМ в концеп- ции современной теории управления выполняется путем решения векторно-матричного уравнения состояния относительно желае- мой, как правило, выходной, переменной СУИМ. Для этой цели применяют матрицу переходных состояний.
Рис. 2.5. Реакция электродвигателя постоянного тока на возмущающее воздействие в виде ступени номинальной нагрузки на валу
Если известны в момент времени t = 0 начальное состояние X (0) объекта управления и вектор U (t) внешних для СУИМ воз- действий, то уравнение движения системы во времени определяет- ся выражением [14, 16]
t X (t ) = Ф (t ) X (0) + ò Ф (t - t) BU (t) d t. 0
(2.6) Первое слагаемое в векторно-матричном выражении (2.6) от- ражает свободное движение многомерной линейной системы управления и аналогично скалярному выражению (2.4), описы- вающему свободное движение одномерной системы. Второе сла- гаемое в формуле (2.6) отражает вынужденное движение много- мерной линейной САУ и аналогично выражению (2.5), описы- вающему вынужденное движение одномерной системы. Матрицу Ф (t), определяющую динамические процессы в сис- теме, называют переходной матрицей состояния или просто мат- рицей перехода. Существует ряд методов нахождения этой матри- цы, базирующихся на описании систем как во временной области (в форме дифференциальных или векторно-матричных уравнений), так и в области комплексного переменного p (в операторной фор- ме или в форме структурных схем). Наиболее часто для определе- ния матрицы перехода во временной области используют матрич- ную экспоненциальную функцию в виде разложения ее в ряд с ог- раниченным числом k (k < ∞) членов ряда [12–16]:
¥ Φ (t ) = exp(A t ) = å k =0 A kt k
k!
= E + A t (A t )2
(A t )3
+... + (A t ) k
+..., где E – единичная матрица;! – знак факториала. Решение векторно-матричного уравнения, описывающего ли- нейную систему управления, можно получить и в области ком- плексного переменного p, применив преобразование Лапласа: X (p) = [ p E - A ]-1 X (0) + [ p E - A ]-1 BU (p), где [ p E - A ]-1
– преобразование Лапласа переходной матрицы состояния, т.е. Φ (p ) = [ p E - A ]-1. В частности, для свободного движения системы под действи- ем ненулевого начального состояния X (0) можно записать X (p) = Φ (p) X (0).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||

 ω ω0 ωн
ω ω0 ωн
 W 1 (p) W 2
W 1 (p) W 2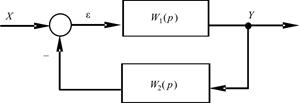

 K i + 1
K i + 1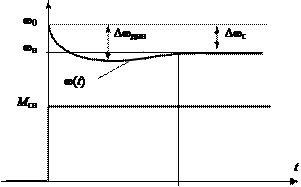 0 t рег
0 t рег
 2!
2!




