
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез контура регулирования скорости.Содержание книги
Поиск на нашем сайте
Структурная схема замкнутого контура регулирования скоро- сти (ЗКРС) приведена на рис. 7.3. Синтез регулятора скорости проведем с применением типовой методики, изложенной выше. В качестве допущения будем полагать, что статическая нагрузка на валу электропривода отсутствует, т.е. i c = 0. 1. Параметрическая декомпозиция объекта управления: – БПВ: T м; – МПВ: T т, T фрс, T фдс; – ЭМПВ: T mс = T т + T фрс + T фдс. 2. Задание критерия качества в виде желаемой передаточной функции разомкнутого контура (рассмотрим два варианта): а) настройка на технический оптимум (ТО):
б) настройка на симметричный оптимум (СО):
U зс
– U с ?
Фильтр
U зт
ЗКРТ
3. Синтез структуры и параметров регулятора:
W pc P W оу (P) W ос (P)
R э K д K с таким образом, структура регулятора скорости – П; – K рс = = K т Т м ; 2 Т mc R э K д K с б) при настройке на симметричный оптимум (СО) передаточ- ная функция регулятора скорости
W оу (P) W ос (P)
8 Т 2 (R K K K Т) Р
– коэффициент передачи регулятора K рс = = K т Т м ; 2 Т mc R э K д K с
– постоянная времени интегрирования Т и
= 8 Т 2 R э K д K с;
– постоянная времени изодромного звена T из = 4 T mс. Заметим, что здесь имеют место лишь два независимых пара- метра, поскольку K рс = T из / T и. 4. Расчет параметров регуляторов скорости. Принципиальные схемы П- и ПИ-регуляторов скорости при- ведены на рис. 7.4, 7.5. Расчету подлежат значения резисторов R зс, R ос, R с и емкости конденсатора C ос. Число параметров принципи- альных схем регуляторов превышает число независимых парамет- ров регуляторов, полученных в результате синтеза (один для П-регулятора скорости и два для ПИ-регулятора скорости). Оче- видно, что при расчете регуляторов скорости, как и при расчете регулятора тока якоря, необходимо задаться какими-то парамет- рами, условиями или соотношениями. Воспользуемся следующей последовательностью:
Рис. 7.4. Принципиальная схема П-регулятора скорости R ос C ос
 U зс U зс
Рис. 7.5. Принципиальная схема ПИ-регулятора скорости
а) зададимся значением емкости C ос в пределах (1…4)10–6 Фа- рады; б) примем, что максимальное напряжение задания, обеспечи- вающее ограничение скорости на допустимом уровне, U зc max = 10 В, т.е. несколько меньше напряжения насыщения операционных уси- лителей; фактически заданием этого напряжения мы однозначно определяем величину контурного коэффициента усиления, т.е. 1 / K c = wmax / U зc max = wmax / 10. в) используем соотношения, справедливые для статических режимов любых операционных усилителей с собственным коэф- фициентом передачи свыше 20 000: U зc max / R зc = U дс max / R с = K с / K дс. Порядок расчета параметров П-регулятора скорости: 1. Зададимся R зс = 10…100 кОм. 2. R с = R зс K дс / K с, где K дс = U дс max / wmax. 3. R ос = K рс R зс = K т T м R зс / 2 T mс R э K д K с = K т T м R с / 2 T mс R э K д K дс. Порядок расчета параметров ПИ-регулятора скорости: 1.
2. R эс = T и C ос = 8 T 2 R K K K т T м C ос. 3. R с = R зс K дс / K с. Примечание: поскольку K рс одинаков для П- и ПИ-регулято- ров скорости, часто целесообразно при расчете параметров ПИ- регулятора сохранить порядок расчета параметров П-регулятора, а затем рассчитать величину емкости конденсатора C ос по формуле C ос = 4 T mс / R ос. Если рассчитанные величины резисторов R зс и R с окажутся менее 1 кОм, необходимо изменить соответствующим образом значение C ос. Величины резисторов и емкостей выбираются из стандартных рядов.
W зкрс (Р) = .
Синтезированную САР с П-регулятором скорости часто назы- вают однократно интегрирующей, поскольку желаемая переда- точная функция разомкнутого контура регулирования содержит интегратор первого порядка. Переходный процесс в САР при скачке задания соответствует реакции фильтра Баттерворта второ- го порядка (предполагается, что ЗКРТ аппроксимирован аперио- дическим звеном первого порядка).
Передаточная функция ЗКРС, настроенного на симметричный оптимум, имеет вид W зкрс (Р) = (4 T m c P +1) K c
8 T mc P (T mc P + 1) + 4 T mc P + 1 Синтезированную САР с ПИ-регулятором скорости часто на- зывают двукратно интегрирующей, поскольку желаемая переда- точная функция разомкнутого контура регулирования содержит интегратор второго порядка. Переходный процесс в САР скорости при скачке задания соответствует кривой 1 на рис. 7.6.
0 3,1
7,0
t / T mс
Рис. 7.6. Переходный процесс в САР скорости при скачке задания
Перерегулирование скорости в линейной зоне работы САР достигает 43 % (предполагается, что ЗКРТ аппроксимирован звеном первого порядка). С целью снижения перерегулирования на входе замкнутой САР скорости устанавливают фильтр (апериодическое звено) первого порядка с постоянной времени 4 T mс: W ф(P) = 1 / 4 T mс P + 1.
W зкрс (Р) = .
Установка фильтра позволяет снизить перерегулирование при скачке задания скорости приблизительно до 8 % при некотором снижении быстродействия системы (см. кривую 2, рис. 7.6). Такая реакция САР соответствует реакции фильтра Баттерворта третьего порядка. На рис. 7.7 приведены реакции одно- и двукратно интегри- рующей САР скорости на ударное приложение нагрузки на валу электропривода.
i c
0
Dwс
Рис. 7.7. Переходные процессы в САР скорости при ударном приложении нагрузки на валу электропривода
Кривые 1, 3 – переходные процессы скорости и тока якоря в однократно интегрирующей системе, кривые 2, 4 – соответст- вующие переходные процессы в двукратно интегрирующей систе- ме. Заметим, что при приложении нагрузки к валу электропривода в однократно интегрирующей системе имеет место статическая ошибка регулирования скорости Dwс. Приближенно величину ста- тической ошибки регулирования скорости можно определить по формуле Dwс = (2 T mc / J пр) D M с, где J пр – приведенный к валу двигателя момент инерции электро- привода; D M с – приложенный к валу двигателя момент статиче- ской нагрузки. Таким образом, чем выше быстродействие ЗКРС (меньше T mc) и больше приведенный момент инерции, тем меньше статическая ошибка регулирования скорости. В двукратно интегрирующей системе статическая ошибка регулирования скорости отсутствует, т.е. она является астатической по нагрузке на валу электроприво- да. Максимальный динамический провал (выброс) скорости в та- кой системе можно оценить по эмпирической формуле Dwд = (1,9 T mc / J пр) D M с.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.139 (0.011 с.) |

 W р жел ( Р) = 1 2 Т mс Р (Т mс Р + 1);
W р жел ( Р) = 1 2 Т mс Р (Т mс Р + 1);


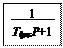
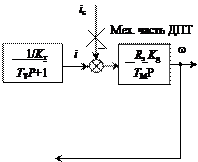 Рис. 7.3. Структурная схема контура регулирования скорости
Рис. 7.3. Структурная схема контура регулирования скорости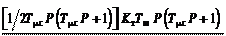 а) при настройке на технический оптимум (ТО) передаточная функция регулятора скорости
а) при настройке на технический оптимум (ТО) передаточная функция регулятора скорости
 = K т Т м ; 2 Т mc R э K д K с
= K т Т м ; 2 Т mc R э K д K с параметр П-регулятора – коэффициент его передачи:
параметр П-регулятора – коэффициент его передачи:
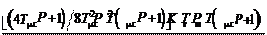
 R э K д K с
R э K д K с Таким образом, структура регулятора скорости – ПИ; пара- метры регулятора:
Таким образом, структура регулятора скорости – ПИ; пара- метры регулятора:
 1
1
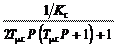 Передаточная функция замкнутого контура регулирования ско- рости (ЗКРС), настроенного на технический оптимум, имеет вид
Передаточная функция замкнутого контура регулирования ско- рости (ЗКРС), настроенного на технический оптимум, имеет вид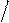 2 2 .
2 2 .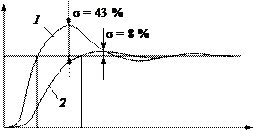 wз
wз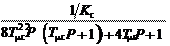 Передаточная функция ЗКРС с предшествующим фильтром на входе приобретает вид
Передаточная функция ЗКРС с предшествующим фильтром на входе приобретает вид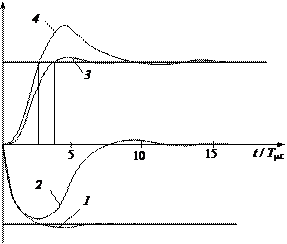 i, w
i, w


