Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод переменного коэффициента усиленияСодержание книги
Поиск на нашем сайте
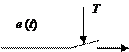
В основе метода лежат теорема об n интервалах дискретного управления и применение дискретных уравнений переходных со- стояний [12, 14]. Дискретный регулятор на начальном этапе синте- за представляется в виде последовательной цепочки, состоящей из квантователя ошибки e (t) регулирования по времени с тактом T, фиксатора Ф нулевого порядка и безынерционного звена с пере- менным коэффициентом Kj усиления (рис. 9.5).
Рис. 9.5. Структура дискретного регулятора на начальном этапе синтеза
Входным воздействием регулятора является ошибка регули- рования e (kT), выходным – сигнал управления u (kT). Ошибка регу- лирования e (kT) на входе звена с переменным коэффициентом усиления обновляется и фиксируется с помощью экстраполятора нулевого порядка с каждым тактом дискретизации Т. Согласно теореме об n интервалах дискретного управления система будет оптимальной по быстродействию (в концепции им- пульсных САУ), если переходные процессы в ней заканчиваются через n тактов управления, причем без перерегулирования выход- ной координаты, где n – порядок линейного объекта управления. Критерий оптимальности системы (максимум быстродействия) в этом случае записывается в виде t рег = nT Þ min. Цель синтеза – определение n значений коэффициента Kj, обеспечивающих дос- тижение предельного быстродействия СУИМ. Для дискретной СУИМ с рассматриваемым регулятором можно записать n дискретных уравнений переходных состояний: V (kT +) = Φ (K j, T) B (T) V ëé(k -1) T ûù, k = 1, 2,..., n, где V [(k –1) T ] – вектор состояния системы на предыдущем такте управления; V (kT +) – вектор состояния на текущем такте управле- ния после замыкания ключевых элементов (фиксации новых зна- чений измеренной координаты и ошибки регулирования); Ф (Kj, Т) – расширенная матрица перехода системы, зависящая от искомых коэффициентов Kj; B (T) – матрица переключения импульсных элементов. В результате решения системы n неоднородных алгебраиче- ских уравнений, составленных из дискретных уравнений состоя- ний, находят численные значения коэффициентов Kj. Для этого применяют различные методики, алгоритмы и численные проце- дуры [12, 14, 17, 22]. На заключительном этапе синтеза оптимальный регулятор представляют в виде дискретной передаточной функции:
u (z) j =0
e (z) n -1 å e jT j =0 +) z - j В отличие от рассмотренного ранее метода синтеза такт управления здесь выбирается исходя из ограничений ресурсов управления (чем меньше требуемое время регулирования, тем большими ресурсами управления должна обладать САУ). В част- ности, для цифровых электромеханических СУИМ в зависимости от регулируемой координаты значение Т находится в пределах 0,01–0,05 с, что позволяет применить для управления микропро- цессорный контроллер с достаточно малым быстродействием. К существенным недостаткам метода следует отнести до- вольно высокую чувствительность синтезированных СУИМ к ва- риациям параметров объекта управления к «чужим» аддитивным воздействиям. Например, система, оптимизированная по критерию быстродействия по задающим воздействиям, может оказаться да- леко не оптимальной в смысле этого критерия при отработке воз- мущающих воздействий. Кроме того, регулирование по отклоне- нию e (t) (ошибке регулирования) не гарантирует необходимой ди- намической точности регулирования при изменении вида задающего воздействия, отличного от принятого при процедуре синтеза. В итоге система оказывается малопригодной при про- граммно-временном и следящем управлении.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.8.76 (0.009 с.) |