
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое описание функциональных элементов суимСодержание книги
Поиск на нашем сайте
Проектирование и исследование характеристик (показателей качества) спроектированных СУИМ, решение задач синтеза и ана- лиза СУИМ базируется на знании математических моделей и объ- ектов, а также устройств управления. Математические модели (ММ) технических средств и систем автоматизации весьма многообразны и могут быть достаточно сложными. В частности, на сложность ММ электромеханических СУИМ влияет множество факторов: тип электропривода, тип СПЭ, тип электродвигателя, число, компоновочные схемы размещения приводов механических подсистем и конструкции передаточных механизмов, принцип и техническая реализация управления и др. Между тем для подавляющего большинства элементов СУИМ математические модели уже разработаны, причем в разных формах и с разной степенью детализации (с различными допуще- ниями), и подробно рассматриваются в соответствующих дисцип- линах: механике, электротехнике, электромеханике, термодинами- ке и т.п. Ниже рассмотрены наиболее распространенные ММ ос- новных элементов СУИМ. СУИМ – динамические системы, содержащие как минимум один вход и один выход и обеспечивающие преобразование вход- ных (задающих и возмущающих) воздействий в выходные (управ- ляемые) переменные. В этом преобразовании может участвовать достаточно большое число динамических элементов, называемых звеньями [13–16]. Характерной особенностью звеньев систем ав- томатического управления (САУ) является однонаправленность, т.е. отсутствие или ничтожное влияние выходных сигналов на входные. Данное обстоятельство позволяет осуществить декомпо- зицию ОУ и СУИМ в целом на ряд достаточно простых динамиче- ских звеньев, описываемых хорошо известными в математике ме- тодами. При этом физическая природа входных и выходных пере- менных звеньев может быть различной. Например, входными (управляющими) воздействиями электродвигателя постоянного тока являются напряжения на обмотках якоря и возбуждения, а выходными переменными – вращающий момент на валу двигателя и скорость его вращения, т.е. осуществляется преобразование электрической энергии в механическую. Для составления уравнений элементов СУИМ используют фундаментальные законы природы, описываемые уравнениями Ньютона, Лагранжа, Ома, Кирхгофа и т.п. При этом для описания элементов СУИМ используют различные формы: – обыкновенные дифференциальные уравнения (для объектов с сосредоточенными параметрами) или дифференциальные урав- нения в частных производных (для объектов с распределенными параметрами); в основе их составления лежат функциональные схемы той или иной степени детализации, в том числе схемы за- мещения; – операторные уравнения, передаточные функции и переда- точные матрицы, т.е. функции комплексной переменной s или оператора p Лапласа (в непрерывных СУИМ), а также передаточ- ные функции комплексной переменной z (в дискретных СУИМ); в основе их составления лежат дифференциальные уравнения или схемы замещения, а результатом их составления являются струк- турные схемы; – векторно-матричные уравнения; в основе их составления лежат дифференциальные уравнения или структурные схемы, а результатом их составления являются структурные схемы про- странства состояний. Для описания и анализа СУИМ могут использоваться также сигнальные графы, частотные характеристики и диаграммы на их основе и др. К основным элементам СУИМ относят исполнительные ме- ханизмы, их приводы, силовые преобразователи энергии, датчики первичной информации, блоки связи (информационные преобра- зователи), преобразователи координат, регуляторы, корректирую- щие динамические звенья, в том числе фильтры.
Исполнительные механизмы Собственно ИМ, будучи механическими устройствами, осу- ществляющими передачу момента или усилия с привода ИМ на РО, могут быть в большинстве случаев представлены простейшей одномассовой механической схемой замещения. Лишь в случае наличия явных упругодиссипативных связей, зазоров, люфтов ме- ханические схемы замещения представляют двух- или трехмассо- вой схемой [17–20]. Схема замещения одномассового ИМ с одно- ступенчатым редуктором приведена на рис. 4.1. М с
М ω φ
Рис. 4.1. Механическая схема замещения одномассового ИМ
На рис. 4.1 введены следующие обозначения: J пр – приведенный к валу электродвигателя момент инерции ИМ,
J пр = J д + J им
ред
(4.1) где J д – момент инерции ротора электродвигателя и ведущей шес- терни; J им – момент инерции исполнительного механизма с ведо- мой шестерней и РО; K ред – коэффициент передачи редуктора; М, М с – соответственно вращающий момент и момент сопротивления на валу электродвигателя; ω, φ – соответственно угловая скорость и угловое положение вала электродвигателя. Уравнения движения ИМ в соответствии со вторым законом Ньютона для вращательного движения и схемой замещения (см. рис. 4.1) имеют вид
(4.2) dt J пр
редw,
(4.3) где ε – угловое ускорение электродвигателя. В электрических исполнительных механизмах (ЭИМ) пе- редача механической энергии с вала электродвигателя на РО осу- ществляется, как правило, с помощью понижающего редуктора, содержащего одну или более кинематических пар. Электрические исполнительные механизмы постоянной ско- рости поворотного и вращательного движения типов МЭО и МЭМ содержат в общем случае цилиндрические, конические, червячные и планетарные передачи. Механизмы прямоходные ти- па МЭП содержат дополнительно выходную кинематическую пару типа «винт – гайка». Сочленение выходного элемента ИМ, пере- дающего перестановочное усилие или вращающий момент регу- лирующему органу (кулачка, рычага, фланца, штока и т.п.), осуще- ствляется различными способами, но такими, которые не допус- кают чрезмерных зазоров и люфтов. В любом случае математическую модель собственно механи- ческой части ИМ постоянной скорости можно представить интег- рирующим звеном:
K ред,
(4.4) где Х (р) – скорость вращения вала электродвигателя ИМ ω(р), рад/с; Y (p) – угловое (рад) перемещение φим(р) или линейное (м) перемещение S им регулирующего органа ИМ; K ред – коэффициент передачи редуктора, имеющий размерность «с» для поворотных и многооборотных ИМ, «м·с/рад» – для прямоходных ИМ. Математические модели исполнительных механизмов пере- менной скорости описываются теми же уравнениями (4.1)–(4.4), однако в отличие от механизмов постоянной скорости (ω ≈ ωн = const) скорость электродвигателя может изменяться с помощью управ- ляемых силовых преобразователей энергии в широком диапазоне (ω = var). Поскольку в таких механизмах выходной координатой обычно является скорость электродвигателя или исполнительного механизма или какая-либо технологическая координата, из модели ИМ исключают уравнения (4.3), (4.4). В этом случае передаточная функция ИМ имеет вид
где X (p) – скорость вращения вала электродвигателя ИМ ω(p), рад/с; Y (p) – угловая ωим(p) или линейная v им(p) скорость движения рабочего органа ИМ (соответственно рад/с или м); K ред – коэффи- циент передачи редуктора, имеющий размерность «м/рад» для ИМ с линейным движением РО, безразмерный – для ИМ с вращатель- ным движением РО. Пневматические исполнительные механизмы (ПИМ), как уже отмечалось в подразд. 1.3, описываются пропорциональным законом движения рабочих органов, т.е. могут быть представлены передаточной функцией
(4.5) где X (p) – давление сжатого воздуха в надмембранной полости МПИМ или в надпоршневой полости цилиндра ППИМ, Па; Y (p) – линейное (м) или угловое (рад) перемещение РО ИМ; K им – коэф- фициент передачи ИМ, имеющий размерность «м/Па» для прямо- ходных РО и «рад/Па» для поворотных РО. Математическая модель электропневматического ИМ (ЭПИМ) может быть представлена также безынерционным про- порциональным звеном с передаточной функцией (4.5), однако входным воздействием Х (р) будет ток управления (обычно в пре- делах 4–20 мА). Гидравлические исполнительные механизмы (ГИМ), как уже отмечалось в подразд. 1.4, описываются интегральным зако- ном движения рабочих органов, т.е. могут быть представлены пе- редаточной функцией
W (р) = Y ( p) = K им, им X (p) р где Х (р) – разность значений давления рабочей жидкости в полос- тях гидроцилиндра ГИМ, Па; Y (p) – линейное (м) или угловое (рад) перемещение РО ИМ; K им – коэффициент передачи ИМ, имеющий размерность «м/Па·с» для прямоходных РО и «рад/Па·с» для поворотных РО. Математическая модель электрогидравлического ИМ (ЭГИМ) может быть представлена безынерционным пропорциональным звеном с передаточной функцией (4.5), где входным воздействием Х (р) является ток управления (обычно в пределах 4–20 мА).
Приводы Поскольку в математических моделях ПИМ и ГИМ как объ- ектов управления учтено действие соответственно пневмо- и гид- роприводов (см. главу 1), в дальнейшем рассматриваются только принципы работы и ММ электроприводов (электрических машин) для ЭИМ с постоянной и переменной скоростью. К приводам ЭИМ относятся следующие типы двигателей: – коллекторные двигатели постоянного тока (ДПТ); – бесколлекторные двигатели постоянного тока (БДПТ); – асинхронные трехфазные и однофазные (АД); – синхронные трехфазные и однофазные (СД); – шаговые (ШД). Коллекторные двигатели постоянного тока. К коллектор- ным двигателям постоянного тока или просто двигателям посто- янного тока (ДПТ) относятся электрические машины, преобра- зующие электрическую энергию питающей сети переменного или постоянного тока в механическую энергию движения рабочих ор- ганов (РО) исполнительных механизмов (ИМ). В системах автоматизации большинства технологических процессов и установок на основе ДПТ для регулирования коорди- нат и параметров технологического процесса применяются сило- вые преобразователи энергии (СПЭ) различного типа в зависимо- сти от требований к электроприводу и его роли в АСУТП. Ниже приведены математические модели коллекторных ДПТ в различных общепринятых в теории управления формах [13–17]. Электродвигатели постоянного тока (ДПТ) представляют со- бой объекты управления, регулируемые в общем случае по цепям якоря и возбуждения [11,12]. Применяются для регулирования скорости и положения рабочих органов как общепромышленных, так и специальных механизмов. Являются приводами ЭИМ с пе- ременной скоростью. Функциональная схема электродвигателя приведена на рис. 4.2, а, а схемы замещения – на рис. 4.2, б, в, г. Применяя декомпозицию ДПТ, нетрудно заметить, что в его структуре имеется три основных подсистемы или цепи: – цепь якоря, питаемая регулируемым напряжением U я; R э, L э – соответственно эквивалентное активное сопротивление и эк- вивалентная индуктивность якорной обмотки; E д – ЭДС электро- двигателя; i я – ток якоря; – цепь возбуждения, питаемая регулируемым напряжением U в; R в, L в – соответственно эквивалентное активное сопротивление и эквивалентная индуктивность обмотки возбуждения; i в – ток возбуждения; – электромеханическая цепь, обеспечивающая преобразова- ние электромагнитной энергии в энергию вращения вала ротора; J д – момент инерции ротора электродвигателя; M, M c – соответст- венно вращающий момент на валу электродвигателя и момент со- противления на его валу; ω – скорость вращения вала двигателя.
Рис. 4.2. Функциональная схема (а) и схемы замещения (б, в, г) электродвигателя постоянного тока
Приведем описание ДПТ в различных формах, что позволит при необходимости легко установить взаимосвязь математических моделей. Для описания динамических моделей электрических цепей электродвигателя (см. рис. 4.2) воспользуемся законами Кирхгофа, а для описания механической цепи – вторым законом Ньютона. Тогда получим систему дифференциальных уравнений:
э ë э (U я - Е д) ù ü - i я ú ,ï
di в = 1 é 1 U
- i ù , ï,
(4.6) dt T ê R в в ú ý в ë в û ï
dt J д ïþ где Т э, Т в – электромагнитные постоянные времени соответственно обмотки якоря и обмотки возбуждения, T = L э, T = L в.
э R в R э в Электромагнитные цепи двигателя взаимосвязаны. При пода- че напряжения U я по цепи якоря протекает ток i я, и при наличии магнитного потока создается электромагнитный момент, вращаю- щий ротор: М = С мФ i я, где С м – конструктивная постоянная двигателя. (4.7) Электромагнитные и механическая цепи также взаимосвяза- ны, так как ток, протекающий по обмотке возбуждения, создает магнитный поток Ф, пронизывающий обмотку якоря и наводящий в ней ЭДС вращения: Е д = С еFw, (4.8) где С е – конструктивная постоянная двигателя, в системе СИ рав- ная по величине С м. Анализируя выражения (4.7), (4.8), заметим, что произведение переменных приводит к нелинейности математической модели электродвигателя, регулируемого одновременно по цепям якоря и возбуждения. Кроме того, при регулировании напряжения воз- буждения двигателя проявляется нелинейный характер изменения потока Ф в функции тока возбуждения i в (намагничивающей силы F = w в i в, где w в – число витков обмотки возбуждения). Кривая на- магничивания ДПТ соответствует нелинейному звену типа «на- сыщение» (рис. 4.3). Рабочая точка с координатами { F 0, Ф0} на кривой насыщения соответствует некоторому, например номинальному, режиму ра- боты ДПТ. ДПТ как нелинейный ОУ, регулируемый по цепям якоря и возбуждения, в соответствии с выражениями (4.6)–(4.9) и рис. 4.3 может быть представлен в виде структурной схемы (рис. 4.4).
0 F 0
Рис. 4.3. Кривая насыщения магнитной цепи ДПТ
Пусть изменения аддитивных (управляющих и возмущаю- щих) воздействий незначительны или, по крайней мере, непрерыв- ны. Тогда нелинейную модель ДПТ целесообразно линеаризовать в окрестности вектора рабочих траекторий и представить в виде линейной модели. В качестве рабочих траекторий примем уравне- ния M 0 = C мФ0 i я0, E д = C еФ0ω0, а все переменные ДПТ будем рас- сматривать в приращениях, т.е. в малой окрестности рабочих тра- екторий, и обозначать через символ приращения ∆. Проведем так- же касательную линеаризацию кривой намагничивания, задавшись координатами { F 0, Ф0} текущей рабочей точки и соответствую- щими приращениями Δ F и ΔФ (см. рис. 4.3).
Рис. 4.4. Структурная схема ДПТ как нелинейного объекта управления, регулируемого по цепям якоря и возбуждения Тогда математическую модель ДПТ можно представить сис- темой уравнений в приращениях: D i я = 1 ì 1 éD U
- С (w DF +F Dw)ù -D ü ü D t T í R ë я е 0 0 û i я ý,ï э î э þ ï D i = 1 æ 1 D - D ö ï в ç U в i я ÷, ý, (4.9) D t T в è R в ø ï Dw = 1 é С (D i ï
D t J пр ë м в0 0 в с û þ где D Е д, D М – приращения координат ЭДС двигателя и электро- магнитного момента вдоль вектора рабочих траекторий, D Е д = С е (w0DF + F0Dw), D М = С м (D i я0DF + F0D i я ); DF – при- ращение магнитного потока, DF= K фD F = K ф w вD i в; K ф – коэффи- циент линеаризации кривой насыщения магнитной цепи, являющий- ся функцией координат рабочей точки (см. рис. 4.3), K ф = DF.
Структурная схема ДПТ, соответствующая уравнениям (4.9), приведена на рис. 4.5.
Δ U в
Δ I в Δ F
Пусть электродвигатель регулируется только по цепи якоря (на- пряжение возбуждения U в = const, а следовательно, Ф = Фн = const). Тогда математическая модель электродвигателя примет вид di я = 1 é 1 (U
- C F w) - i ù ,ü dt T ê R я e н я ú ï э ë э û ï (4.10)
- М ). ï dt J д м н я с ïþ Математическая модель в виде формул (4.10) описывает ДПТ как линейный объект второго порядка. Для перехода от дифференциальных уравнений (4.10) к опе- раторным произведем замену d = p. Тогда получим
pi = 1 é 1 (U - C F w) - i ù ,ü я T ê R я e н я ú ï э ë э û ï (4.11)
д þ По операторным уравнениям (4.11) составим структурную схему электродвигателя, приведенную на рис. 4.6. Как видим, структурная схема ДПТ, регулируемого по цепи якоря, содержит четыре типовых линейных динамических звена: апериодическое, интегрирующее и два безынерционных, а также два суммирующих звена.
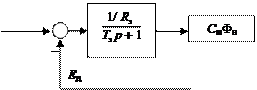 U я i я U я i я
Рис. 4.6. Структурная схема ДПТ, регулируемого по цепи якоря Приведем векторно-матричное описание ДПТ как объекта регулирования по цепи якоря, т.е. будем полагать, что напряжение возбуждения U в = const, а магнитный поток Ф = Фн. Воспользуемся векторно-матричной моделью [12, 13, 16] ли- нейных САУ в виде Х (t ) = AХ (t ) + BU (t ) + CF (t ), (4.12) где Х (t ), U (t ), F (t ) – векторы соответственно состояния, управ- ления и возмущения САУ; X (t) = éë x 1 (t) x 2 (t)... xn (t)ùû¢ , U (t) = ëé u 1 (t) u 2 (t)... um (t)ûù¢ , F (t) = éë f 1 (t) f 2 (t)... fd (t)ûù¢ , «′» – символ транспонирования; А, В, С – стационарные матрицы соответственно состояния, управления и возмущения, é a 11 a 12 ... a 1 n ù é b 11 b 12 ... b 1 m ù é c 11 c 12 ... c 1 d ù ê a a ... a ú ê b b ... b ú ê c c ... c ú А = ê 21 22 2 n ú , B = ê 21 22 2 m ú , C = ê 21 22 2 d ú. ê ...... ... ... ú ê ...... ...... ú ê ...... ...... ú ê a a ... a ú ê b b ... a ú ê c c ... c ú ë n 1 n 2 nn û ë n 1 n 2 nm û ë n 1 n 2 nd û Зададимся векторами состояния, управления и возмущения в виде X (t ) = éë x 1 (t ) x 2 (t )ùû¢ = éë i я (t ) w(t )ûù¢ ; U (t ) = u 1 (t ) = U я (t ); F (t) = f 1 (t) = М с (t),
(4.13) По уравнениям (4.10)–(4.13) найдем матрицы состояния, управления и возмущения: é - 1 - С еФ ù
é 1 ù
é 0 ù
А = ê э э э ú; В = ê Т R ú; С = ê 1 ú. ê C Ф ú ê э э ú ê- ú
ê м 0 ú ëê 0 úû ëê J д úû ë J д û Бесколлекторные двигатели постоянного тока. Бесколлек- торные двигателя постоянного тока (БДПТ) с возбуждением от постоянных магнитов (brush-less direct current motor with permanent magnets) часто еще называют вентильными двигателями (ВД). При контроле и преобразовании координаты положения ИМ их приня- то называть сервоприводами постоянного тока. Эта машина по своей конструкции ничем не отличается от классического синхронного двигателя с постоянными магнитами (СДПМ), изменен лишь принцип питания. Если СДПМ питается от источника переменного тока или напряжения, как правило, фор- мируемого при помощи ШИМ, то ВД – трапецеидальным напря- жением, питающим соответствующие фазы двигателя и переклю- чаемым по мере поворота ротора. Являются приводами ЭИМ с переменной скоростью. Функ- циональная схема электродвигателя приведена на рис. 4.7.
Рис. 4.7. Функциональная схема БДПТ ствительных элементов равно числу обмоток статора. Датчик положения ротора предназна- чен для выработки сигналов управления моментами времени и по- следовательностью коммутации токов в обмотках статора. Управление двигателем основано на принципе частотного ре- гулирования с самосинхронизацией, суть которого заключается в управлении вектором магнитного поля статора в зависимости от положения ротора. Данный тип двигателей был создан с целью улучшения свойств коллекторных электродвигателей постоянного тока. Бесколлекторный двигатель объединяет в себе лучшие каче- ства бесконтактных двигателей и двигателей постоянного тока. Основными достоинствами вентильных двигателей являются следующие: – высокие быстродействие и точность позиционирования; – широкий диапазон изменения частоты вращения; – большая перегрузочная способность по моменту; – большой срок службы, высокая надежность и повышенный ре- сурс работы за счет отсутствия скользящих электрических контактов; – низкий перегрев электродвигателя при работе в режимах с возможными перегрузками; – высокая надежность работы, поскольку отсутствует щеточ- ный узел; – большой ресурс электродвигателя ограничен в основном только ресурсом подшипников; – линейность регулировочной характеристики и меньший уровень электромагнитного шума по сравнению с коллекторными двигателями постоянного тока; – применение в конструкции электродвигателя балансировоч- ных колец потенциально может обеспечить стабильность работы при очень высоких скоростях вращения (десятки тысяч оборотов в минуту). – отсутствие искрообразующих элементов и, как следствие, высокая взрывобезопасность делают бесколлекторные двигатели идеальным силовым элементом в запорном оборудовании нефте- и газопроводов. Бесколлекторные двигатели не имеют недостатков, присущих асинхронным двигателям (потребление реактивной мощности, по- тери в роторе) и синхронным двигателям (пульсация частоты вра- щения, выпадение из синхронизма). В отличие от шаговых двига- телей БДПТ не требует сложных схем управления. Как и у коллекторных двигателей, момент бесколлекторных двигателей прямо пропорционален току, а скорость зависит от на- пряжения питания и нагружающего момента. СУИМ на основе БДПТ находят широкое применение в робо- тотехнике, поскольку наличие встроенного датчика угла поворота позволяет создавать обратную связь по положению рабочих орга- нов и делает бесколлекторный двигатель удобным при построении систем автоматического управления. БДПТ на российском рынке представлены несколькими се- риями, в частности сериями FL42BLS (питание напряжением ~24 В), FL57BL(S) (питание напряжением ~36 В), FL86BLS (пита- ние напряжением ~48 В) мощностью от 26 до 660 Вт и скоростью вращения 3–4 тыс. об/мин. Серии FL57BL-JB и FL86BLS-JB име- ют встроенный редуктор с коэффициентом редукции от 20 до 1333, некоторые серии имеют встроенные блоки управления (драйверы), формирующие управляющие сигналы «разрешение», «направление» и «торможение». На российский рынок БДПТ поставляются НПФ Stepmotor, НПФ «Электропривод», НПО «Атом» и др. В табл. 4.1 в качестве примера приведены характеристики бесколлекторных электродвигателей серии FL42BL.
Таблица 4.1 Характеристики бесколлекторных электродвигателей FL42BL
Окончание табл. 4.1
Внешний вид бесколлекторного электродвигателя FL42BL приведен на рис. 4.8.
нии БДПТ примем во внимание следующее: – процессами коммутации си- ловых обмоток якоря, располо- женных на неподвижном статоре, Рис. 4.8. Внешний вид БДПТ FL42BL можно пренебречь, поскольку переключение осуществляется пол- ностью управляемыми бесконтактными ключами; – быстродействие БДПТ много выше, чем быстродействие ИМ (быстродействие изменения положения РО); – быстродействие БДПТ много выше, чем быстродействие изменения технологических координат СУИМ (температуры, дав- ления, расхода, уровня и др.); – механическая характеристика двигателя жесткая, во многом похожа на характеристику коллекторного ДПТ. Таблица 4.2 Назначение выводов кабеля
С учетом изложенного математическую модель привода можно рассматривать безынерционной пропорциональной, т.е. передаточная функция БДПТ имеет вид Y (p) w (p) W БДПТ (р) = = = K БДПТ , X (p) U п (p) где ω(р) – скорость вращения электродвигателя, рад/с; U п(р) – среднее значение напряжения питания обмоток, В; K БДПТ – коэф- фициент передачи БДПТ, рад/В·с. Асинхронные двигатели. Асинхронные двигатели относятся к двигателям переменного тока, принимающим главенствующее участие в управлении технологическими процессами и производ- ственными установками (более 70 % всех ЭИМ оснащены именно ими). Различают: – асинхронные двигатели с короткозамкнутым ротором (АДКР), питающиеся от трехфазной сети переменного тока (~220 В и более); – асинхронные двигатели с фазным ротором (АДФР), питаю- щиеся от трехфазной сети переменного тока (~220 В и более); – асинхронные двигатели с короткозамкнутым ротором и до- полнительной пусковой обмоткой на статоре, питающиеся от од- нофазной сети переменного тока (~220 В и более).
~ U 1
~ U 1 ~ U 1
а б в Рис. 4.9. Функциональные схемы асинхронных двигателей: а – АДКР; б – АДФР; в – АДКР с однофазным питанием; ~ U 1 – переменное напряжение статорной обмотки (трех- или однофазное); M – вращающий момент; M c – момент сопротивления на валу двигателя; ω – скорость вращения двигателя; Р – рабочая обмотка; П – пусковая обмотка; С – емкость фазосдвигающего элемента (подбирают таким образом, чтобы токи в рабочей и пусковой обмотках различались по фазе на 90°)
Эти электродвигатели работают как в системах постоян- ной, так и в системах переменной скорости ИМ. Скорость n 2 вращения ротора асинхронной машины отстает от скорости n 1 поля статора и может быть определена по формуле [17–19] n = n (1 - S) = 60 f 1 (1 - S),
(4.14) 2 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.217.179 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


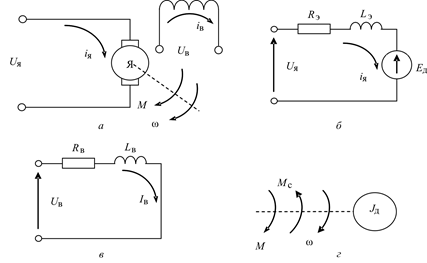
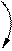 J пр
J пр 


 d w = K dt
d w = K dt р
р





 Ф
Ф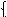 ΔФ Ф0
ΔФ Ф0 M c
M c
 D F
D F

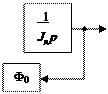 Δω
Δω



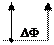


 dt
dt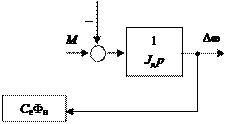 M c
M c
 ê Т Т R ú
ê Т Т R ú 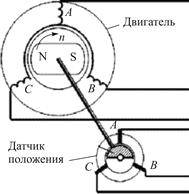 Представленный БДПТ со- стоит из статора с трехфазной обмоткой, соединенной в звез- ду, и возбужденного ротора в виде постоянного магнита, а также датчика положения ро- тора, выполненного в одном корпусе с двигателем. Датчик положения ротора выполнен с одним и тремя чувствитель- ными элементами. Число чув-
Представленный БДПТ со- стоит из статора с трехфазной обмоткой, соединенной в звез- ду, и возбужденного ротора в виде постоянного магнита, а также датчика положения ро- тора, выполненного в одном корпусе с двигателем. Датчик положения ротора выполнен с одним и тремя чувствитель- ными элементами. Число чув- Датчик положения ротора вы- полнен на основе датчиков Холла. В табл. 4.2 приведено назначение выводов кабеля БДПТ (см. рис. 4.8). При математическом описа-
Датчик положения ротора вы- полнен на основе датчиков Холла. В табл. 4.2 приведено назначение выводов кабеля БДПТ (см. рис. 4.8). При математическом описа-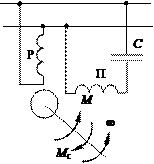 Функциональные схемы асинхронных двигателей ЭИМ при- ведены на рис. 4.9.
Функциональные схемы асинхронных двигателей ЭИМ при- ведены на рис. 4.9.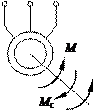
 ω ω
ω ω



