
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальные настройки контуров регулированияСодержание книги
Поиск на нашем сайте
В многоконтурных электромеханических системах подчинен- ного регулирования координат наиболее распространены настрой- ки отдельных контуров на технический (модульный), симметрич- ный и апериодический оптимумы [16–18, 23]. Технический оптимум При настройке контуров регулирования СУИМ на техни- ческий оптимум (ТО) передаточную функцию замкнутого контура регулирования представляют в виде фильтра Баттерворта второго порядка:
Передаточная функция разомкнутого контура имеет вид
(6.1)
W pег (р) = . (6.2)
Переходный процесс в младшем контуре регулирования представлен кривой 1 на рис. 6.2.
2 1
4,3 % 8 %
1 3 0 3,1 T m 4,7 T m
7,1 T m t Рис. 6.2. Кривые оптимальных переходных процессов контуров регулирования СУИМ
Время регулирования младшего контура составляет около 8 T m, в остальных контурах при той же настройке оно будет как ми- нимум в 2 i –1 раз больше, i = 2, …, n. Симметричный оптимум
éë8 T 2 p 2 (T p + 1) + 4 T p + 1ùû K.
4 Т m р
W ( р) = (4 T p + 1) 8 T 2 p 2 (T p + 1); (6.3) p
W pег (р) = m m m
2 2 . 8 T m p (T m p + 1) W oy ( р) Такая настройка контуров регулирования обеспечивает аста- тизм первого порядка по задающим воздействиям (теоретически нулевую установившуюся ошибку регулирования выходной коор- динаты). Однако отработка скачкообразных задающих воздейст- вий сопровождается высоким перерегулированием выходной ко- ординаты контура, достигающим 56 % (кривая 2 на рис. 6.2). Для снижения перерегулирования на вход замкнутого контура регули- рования устанавливают апериодическое звено (предшествующий фильтр первого порядка с постоянной времени 4 Т m ). Переходный
процесс в СУИМ с предшествующим фильтром первого порядка представлен кривой 3 на рис. 6.2. Время регулирования для реак- ций 2 и 3 составляет около 15 Т m . Апериодический оптимум Апериодический оптимум (АО) контуров регулирования применяют, когда перерегулирование выходной координаты должно отсутствовать (многие СУИМ не допускают перерегули- рования, например, по координатам положения РО, температуры, давления и т.п.). В зависимости от желаемого порядка n настроенного контура различают апериодические оптимумы первого, второго и третьего порядка. Для n = 1 имеем
(6.4)
W pег (р) =
(р).
Для n = 2 имеем m oy
(6.5)
W pег
Для n = 3 имеем (р) = .
(6.6)
W pег (р) = é Т 2 р 2 (Т р + 3) + Т р ù W .
ë m m m û oy Кривые переходных процессов в апериодических системах первого, второго и третьего порядка приведены на рис. 6.3 и обо- значены соответствующими цифрами (см. кривые 1, 2, 3).
4 T m
8 T m t Рис. 6.3. Кривые переходных процессов в апериодических системах первого, второго и третьего порядка
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.215.5 (0.01 с.) |

 W з ( р) = 1 éë2 Т m р (Т m р + 1) + 1ùû K oc.
W з ( р) = 1 éë2 Т m р (Т m р + 1) + 1ùû K oc.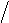 W p ( р) = 1 2 Т m р (Т m р + 1).
W p ( р) = 1 2 Т m р (Т m р + 1). Передаточная функция оптимального регулятора в этом случае имеет вид
Передаточная функция оптимального регулятора в этом случае имеет вид 56 %
56 %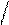 При настройке контуров регулирования многоконтурной СУИМ на симметричный оптимум (СО) их передаточные функции представляют в виде оптимальных звеньев третьего порядка:
При настройке контуров регулирования многоконтурной СУИМ на симметричный оптимум (СО) их передаточные функции представляют в виде оптимальных звеньев третьего порядка:
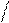 т.е. в виде
т.е. в виде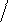 (4 Т m р +1) W o c
(4 Т m р +1) W o c 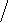 W з ( р) = 1 (Т m р + 1) K oc;
W з ( р) = 1 (Т m р + 1) K oc;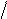 W p (р) = 1 Т m р;
W p (р) = 1 Т m р;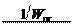 T pW
T pW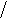
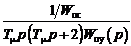 W p ( р) = 1 Т m р (Т m р + 2);
W p ( р) = 1 Т m р (Т m р + 2);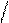 W з ( р) = 1 (Т m р + 1)(Т m р + 1)(Т m р + 1) K oc;
W з ( р) = 1 (Т m р + 1)(Т m р + 1)(Т m р + 1) K oc;
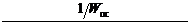 (р)
(р) 0
0


