Метод аналитического конструирования цифровых регуляторов состояния

Многие системы управления относятся к классу систем, функционирующих в режимах малых отклонений координат: сис- тем стабилизации той или иной технологической координаты (скорости вращения или перемещения рабочего органа, темпера- туры, давления, натяжения и т.п.), следящих систем управления, систем воспроизведения движений. Поскольку основным техноло- гическим требованием при синтезе таких систем является макси- мальное быстродействие и минимум динамической ошибки отра- ботки рассогласований заданных и действительных значений ко- ординат состояния, в качестве дискретного критерия

оптимальности часто принимают критерий вида

J = n ® min,

где

п – число периодов дискретного управления, по истечении кото- рых система приходит в установившееся состояние без перерегу- лирования выходной переменной [14, 29, 30].

Синтез апериодических динамических систем, а именно та- кими являются системы, гарантирующие отсутствие перерегули- рования в замкнутых дискретных САУ, традиционно проводят на основе идеальной компенсации нулей и полюсов объекта управле- ния полюсами и нулями дискретной передаточной функции регу- лятора, а также добавления новых полюсов и нулей в соответст- вующих областях Z -плоскости [12–14]. Неточность математиче- ского описания, временной и температурный дрейф параметров объекта управления, ограничения в реализации передаточной функции регулятора техническими средствами приводят к неус- тойчивости замкнутой системы. Более того, такая процедура син- теза СУИМ даже при идеальной компенсации полюсов и нулей предполагает «апериодичность» переходных процессов только по отношению к входным воздействиям определенного вида и места их приложения. По отношению к «чужим» входным воздействиям система может иметь неприемлемое качество. В этой связи синтез СУИМ осуществляют на основе контроля полного состояния сис- темы и реализации апериодических регуляторов состояния.

Ниже рассмотрена аналитическая процедура синтеза аперио- дических регуляторов состояния, обеспечивающих апериодиче- ские переходные процессы в линейных системах произвольного порядка. Предлагаемая процедура синтеза теоретически обеспечи- вает в системе управления астатизм первого порядка по задающим воздействиям, а следовательно, повышенную точность отработки изменяющихся во времени задающих воздействий.

Пусть линейный стационарный объект управления описыва- ется дискретно-непрерывным векторно-матричным уравнением

X  (t) =  AX (t ) +  BU (kT ) +  CF (t ),

(9.6)

где

X (t), U (kT), F (t)

– векторы состояния, управления и возму-

щения соответственно размерностей

n ´1, m ´1, d ´1;

А, В, С –

матрицы состояния, управления, возмущения размерностей

n ´ n, n ´ m, n ´ d

соответственно; T – такт дискретного управления;

k – номер такта дискретного управления.

Задача синтеза формулируется следующим образом: необхо- димо для произвольных начальных значений Х (0), F (0) и постоян- ного на интервале nT вектора возмущений F( t) сформировать дис- кретную управляющую последовательность (U kT), k = 0, 1,..., пе- реводящую объект управления (9.6) в заданное конечное состояние Х ^* за n тактов управления, где n – порядок динамиче- ского объекта. Допущения при синтезе оптимального управления: время измерения координат состояния и выработки (вычисления) координаты управления ничтожно мало в сравнении с тактом T управления; длина разрядной сетки ЭВМ и устройств связи с объ- ектом управления позволяет пренебречь квантованием непрерыв- ных сигналов по уровню; значение периода управления T предпо- лагается априори выбранным исходя из ограничений ресурсов управления. Приведенные допущения являются широко распро- страненными при синтезе дискретных систем управления объек- тами рассматриваемого класса [12, 29].

Представим искомую управляющую дискретную последова- тельность в виде линейной формы дискретных значений векторов состояния X (kT), задающих воздействий X ^*(kT), вектора возмуще-

ния F (kT) и вектора производных задающих воздействий в виде

X  * (kT )

U (kT ) =  αX (kT ) +  βX ^* (kT ) +  γF (kT ) +  δX  * (kT ).

(9.7)

В этом уравнении α, β, γ, δ – матрицы соответственно раз-

мерностей

m ´ n, m ´ m, m ´ d, m ´ m,

определение которых и явля-

ется задачей синтеза.

Предлагаемый подход основан на разных формах представле- ния объекта управления (в виде непрерывной модели) и устройст- ва управления (в виде дискретной модели), причем структура уст- ройства управления предполагается заданной не в виде дискретной передаточной функции, а в виде линейного дискретного регулято- ра состояния системы.

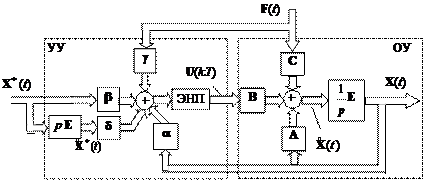
Векторная структурная схема такой дискретно-непрерывной системы приведена на рис. 9.6.

 

Рис. 9.6. Векторная структурная схема дискретно-непрерывной САУ

 

Пунктирными линиями на схеме выделены объект управле- ния (ОУ) и устройство управления (УУ) – дискретный регулятор состояния. Дискретизация вектора управления и, соответственно, всех аддитивных воздействий осуществляется в моменты времени kT (k = 0, 1, 2, …) методом интерполяции нулевого порядка. Экст- раполятор (фиксатор) нулевого порядка обозначен на схеме аббре- виатурой ЭНП. Простейшая аппаратная реализация векторного ЭНП – m устройств выборки-хранения, имеющих общий квантова- тель сигналов в моменты времени kT (m – размерность вектора управления). При микропроцессорной реализации дискретного регулятора состояния ЭНП – совокупность регистров памяти с пе- резаписью информации с тактом T управления.

Заметим, что линейность моделей (9.6) объекта управления    и регулятора (9.7) состояния объекта управления позволяет при

синтезе САУ применить принцип суперпозиции управляемых ди- намических процессов. Проведем декомпозицию управляющей дискретной последовательности и динамических процессов в сис- теме на две составляющие – управляемый свободный процесс и управляемый вынужденный процесс. В соответствии с этим в процедуре синтеза выделим два этапа – синтез свободного и син- тез вынужденного движения.