Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
САР положения с нелинейным регуляторомСодержание книги
Поиск на нашем сайте
Режим средних и больших перемещений характеризуется вы- ходом как минимум ускорения двигателя на режим ограничений, т.е. emax = (d w/ dt)max = (M max + M c)/ J пр (полагаем статическую на- грузку на валу электродвигателя постоянной). В этом случае СУ- ИМ становится нелинейной. Следовательно, для синтеза регулято- ра положения теория линейных систем неприменима, а сам регу- лятор не может быть представлен передаточной функцией. Установим соотношение между скоростью начала торможе- ния wнт и приращением перемещения Djт в режиме средних пере- мещений (см. рис. 8.1, б):
Dj = K t нт +D t
w dt = K j J пр
0
K j J 2
= - K w2 j нт, т j ò М + M ò 2(М
t нт max c wнт max c max где t нт, D t – время начала торможения и время торможения. Отображение полученного выражения на плоскости коорди- нат wнт и Djт называется фазовым портретом (рис. 8.4). Относительно конкретной точки А фазового портрета (см. рис. 8.4) найдем выражение для коэффициента передачи регу- лятора положения:
= K cwнт = 2 K cemax.
(8.2)
п п т п j нт Как видим, коэффициент передачи РП в режиме средних пе- ремещений зависит от скорости начала торможения wнт и пред- ставляет собой нелинейное звено. При малых перемещениях ко- эффициент передачи звена стремится к бесконечности, что сделает позиционную САР неустойчивой. Для обеспечения постоянст- ва K рп и устойчивости системы во всем диапазоне средних пере- мещений принимают wнт = wmax, т.е.
Рис. 8.4. Фазовый портрет позиционной САР для режима средних перемещений
K п K jwmax Заметим, что emax = wmax / D t min. Сравнивая выражения для K рп в режимах малых и средних перемещений, можно убедиться, что время разгона (торможения) до максимальной скорости при на- стройке контура положения на АО D t min ³ 8 T mп, а следовательно, необходимо учитывать фактор ограничения максимального уско- рения emax электропривода при аппроксимации регулятора поло- жения линейным пропорциональным звеном. При такой настройке РП система остается линейной в режи- мах малых и средних перемещений, однако оптимальное по быст- родействию (производительности) позиционирование возможно только при wнт = wmax, т.е. лишь в одной точке фазового портрета. При меньших перемещениях позиционирование будет осуществ- ляться с дотягиванием, при больших – с перерегулированием. Очевидно, что оптимальное позиционирование во всех трех ре- жимах перемещений требует применения нелинейного регулятора положения.
Сделаем допущение, что статическая ошибка позиционирова- ния в ЗКРП отсутствует и ЗКРС имеет достаточное быстродейст- вие. В этом случае выходное напряжение регулятора положения для момента времени, соответствующего началу торможения, можно представить в виде U рп = K рпD U п = K cwнт. Подставляя в это соотношение выражение (8.2) для K рп в ре- жиме средних перемещений, получим
или
2
2
K п K j
D U п
рп c pп
где K ¢рп – постоянный коэффициент передачи параболического ре-
Таким образом, оптимальный нелинейный регулятор положе- ния для режима средних перемещений представляет собой нели- нейность типа «корень квадратный», получивший название «пара- болический регулятор». Режим больших перемещений характеризуется позициониро- ванием с предельно допустимой скоростью wmax, что достигается ограничением выходного сигнала регулятора скорости на уровне U рп = K cwmax. Функциональная зависимость «вход-выход» нели- нейного регулятора, обеспечивающего оптимальное качество ре- гулирования положения рабочего органа при позиционировании во всех трех режимах, приведена на рис. 8.5. В режиме средних перемещений (РСП) характеристика РП имеет нелинейность типа «корень квадратный», в режиме больших перемещений (РБП) – нелинейность типа «насыщение» (на уровне K cwmax), в режиме малых перемещений (РМП) характеристика РП имеет линейную зависимость с коэффициентом передачи, обеспе- чивающим оптимальную настройку ЗКРП на АО в режиме малых перемещений, т.е. K рп = K c .
mп j п
Рис. 8.5. Характеристика «вход-выход» параболического регулятора положения Нелинейная характеристика такого РП реализуется включе- нием диодно-резистивной матрицы в обратную связь операцион- ного усилителя или программно в микропроцессорных СУИМ.
8.4. Инвариантные и квазиинвариантные следящие СУИМ
Рассмотрим структурную схему следящей системы с подчи- ненным контуром регулирования скорости электропривода (рис. 8.6). Рис. 8.6. Структурная схема следящей СУИМ с подчиненным контуром регулирования скорости
Воздействие статической нагрузки M с на валу электропривода здесь приведено к выходу замкнутого контура регулирования ско- рости (ЗКРС).
W зкрс (Р) = .
Передаточная функция W мс(P) в этом случае может быть по- лучена из рассмотрения структурной схемы ЗКРС, приведенной на рис. 7.3, в которой W (Р) = K = K рс T м .
рс рс 2 T mc R э K д K с Полагая U зс = 0 и принимая во внимание, что M c = i c / K д, по- лучим
W мс (Р) = .
зкрс c мс А ( Р) = 2 Т mс Р (2 Т mс Р + 1) + 1; Тогда получим mс э д м B (Р) = 2 Т mс Р + 1. W (Р) = K зкрс, W
( Р) = K мс В (Р).
зкрс A (P) мс A (P) Если ЗКРС настроен на СО, т.е. применен ПИ-регулятор ско- рости, и на его входе установлен фильтр с постоянной времени 4 T mc, то его передаточная функция имеет вид
W зкрс (Р) = 4 T P é2 T P (T P + 1) + 1ù + 1.
Передаточная функция W мс(P) может быть получена анало- гично предыдущему случаю из рассмотрения структурной схемы ЗКРС, приведенной на рис. 7.3, в которой
W рс (Р) = 4 T mc Р + 1 .
W мс (Р) = 4 T Р é2 T Р (T Р + 1) + 1ù + 1. mc ë mc mc û Введем обозначения: K = 1/ K; K = 2 T R K 2 / T; зкрc с мс μc э д м A (P) = 4 T μc P [2 T μc P (T μc P + 1) + 1] + 1; B (P) = 4 T μc P (T μc P + 1), позволяющие получить те же обобщенные выражения для W зкрс(P) и W мс(P): W (Р) = K зкрс, W
( Р) = K мс В (Р).
зкрс A (P) мс A (P) С учетом обозначений структурной схемы (см. рис. 8.6) и введенных обозначений можно записать j(Р) = K j K зкрс W (Р) K Dj(Р) - K j K мс В (Р) М (Р).
рп п P А (Р) с
А (Р) Р + K j K зкрс K рп K п (Р) + K j K мс В (Р) + М с (Р), j зкрс рп п где j& з – задание перемещения с постоянной скоростью («постоян- ная заводка»), j& з = wз. Пусть ЗКРС настроен на ТО. Для квазиустановившегося ре- жима (P = 0) получим величину установившейся ошибки следящей САУ: Djуст = 1
j& з + K мс
М с.
(8.3) j зкрс рп п зкрс рп п Данное выражение позволяет рассчитать добротность следя- щей системы по скорости в соответствии с выражениями (5.2):
= j& з
= K K K K.
j зкрс рп п Подставляя в данное выражение значение K рп, рассчитанное по выражению (8.1) для системы, настроенной на АО, и значение K зкрс = 1/ K с, получим
Выражения (5.3) и (8.3) позволяют рассчитать добротность следящей системы по моменту статической нагрузки на валу элек- тропривода:
мс Dj mп уст мс j мс Таким образом, для снижения Djуст, а следовательно, для уве- личения добротности следящей СУИМ необходимо увеличивать быстродействие замкнутого контура регулирования положения (ЗКРП) за счет повышения быстродействия внутренних контуров регулирования тока и скорости. Это предполагает применение ма- лоинерционных силовых и информационных преобразователей, а также реализацию оптимальных по быстродействию алгоритмов управления. Величина добротности системы по моменту опреде- ляется не только быстродействием ЗКРП, но и величиной K j K мс. Эффективным средством повышения точности следящих сис- тем управления является применение комбинированного управле- ния, обеспечивающего инвариантность (квазиинвариантность) СУИМ по отношению к задающим и возмущающим воздействиям. Структурная схема такой системы приведена на рис. 8.7.
Рис. 8.7. Структурная схема инвариантной следящей СУИМ В структуру следящей системы управления введено два звена компенсации влияния задающего и возмущающего воздействий (W к1(P) и W к2(P)). Инвариантность системы к изменению задающе- го воздействия обеспечивает звено W к1(P), инвариантность к изме- нению возмущающего воздействия – звено W к2(P). Для нахождения передаточных функций этих звеньев вос- пользуемся принципом суперпозиции. Сначала будем полагать, что M с = 0. Тогда можно записать j(P) = (K j / P) W зкрс(P)[ U рп(P) + U к1(P)] = = (K j / P) W зкрс(P)[ W рп(P) K п Dj (P) + W к1(P) jз(P)]. Полагая, что в инвариантной СУИМ Dj (P) = 0, j(P) = jз(P), получим j з(P) = (K j / P) W зкрс(P)[ W к1(P) jз(P)]. Отсюда W к1(P) = P / K j W зкрс(P). Для нахождения W к2(P) будем полагать jз(P) = 0. Тогда мож- но записать j(P) = (K j / P)[– W мс(P) M с(P) + W к2(P) W рп(P) W зкрс(P) M с(P)] = 0. Отсюда W к2(P) = W мс(P) / W рп(P) W зкрс(P). Заметим, что для обеспечения полной инвариантности следя- щей системы по отношению к задающим и возмущающим воздей- ствиям требуется формирование «чистых» производных этих воз- действий. Если ЗКРС имеет достаточно высокое быстродействие и может быть представлен апериодическим звеном первого поряд- ка в виде W зкрс(P) = (1 / K c) / (T c P + 1), то для обеспечения полной инвариантности и, соответственно, астатизма бесконечно высоко- го порядка по задающему воздействию необходимо ввести первую и вторую производные от задающего воздействия. В действительности ММ ЗКРС может существенно отличать- ся от принятой модели в силу целого ряда факторов: температур- ного и временного дрейфа параметров якорной цепи двигателя, наличия дискретности и неполной управляемости тиристорного
Проблема обеспечения полной инвариантности СУИМ к воз- мущающим воздействиям усугубляется сложностью получения достаточно точной оценки самого возмущения – сигнала, пропор- ционального статической нагрузке на валу двигателя. Все это при- водит к тому, что на практике, как правило, ограничиваются вве- дением в закон управления лишь первых производных задающего и возмущающего воздействий, а следовательно, полученные пере- даточные функции W к1(P) и W к2(P) аппроксимируют пропорцио- нально-дифференциальными (ПД) звеньями. Следящая СУИМ с комбинированным управлением, содер- жащая такие звенья, позволяет практически достичь астатизма первого порядка по задающему и возмущающему воздействиям (скоростная и моментная ошибки отсутствуют). При этом система приобретает качества, подобные введению интегратора в структу- ру регулятора положения. Важно отметить, что введение компен- сирующих звеньев не изменяет характеристического уравнения системы, замкнутой по положению, а следовательно, не оказывает влияния на устойчивость следящей системы. Система комбиниро- ванного управления с упрощенной структурой компенсирующих звеньев обеспечивает частичную инвариантность по отношению к задающим и возмущающим воздействиям и носит название квази- инвариантной по отношению к этим воздействиям.
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СУИМ Электромеханические объекты управления, как отмечалось в главах 3 и 4, представляют, как правило, линейными или нели- нейными непрерывными моделями. Вместе с тем само устройство управления может быть как непрерывным (аналоговым), так и дискретным. Дискретный характер управления позволяет реали- зовать ряд преимуществ, недостижимых для непрерывных СУИМ. Это возможность реализации алгоритмов управления практически любой сложности, реализации максимального быстродействия или точности, возможность перенастройки и автонастройки устройства управления, возможность самодиагностики, управления по про- мышленной сети и др. К дискретно-непрерывным СУИМ относятся релейные (ре- лейно-импульсные) и цифровые СУИМ. Первые применяются преимущественно для управления ЭИМ постоянной скорости (см. подразд. 5.2), вторые – ЭИМ переменной скорости (см. главу 6). Вместе с тем микропроцессорные контроллеры, а следовательно, цифровые средства автоматизации применяются и в тех, и других СУИМ, реализуя разные алгоритмы управления.
9.1. Дискретизация сигналов и Z -преобразование В дискретных и дискретно-непрерывных системах в отличие от непрерывных имеется хотя бы одна координата состояния или управления, имеющая дискретный характер. Достаточным условием дискретности систем управления явля- ется разрывная статическая характеристика. На рис. 9.1 приведена типовая функциональная схема дискретно-непрерывной СУИМ.
Обозначения на рис. 9.1: ДЭ – дискретный элемент; НЧ – непрерывная часть; x (t) – входной непрерывный сигнал; e (t) – непрерывный сигнал ошибки; u* (t) – дискретный сигнал; y (t) – непрерывный выходной сигнал.
– u *(t)
y (t)
Звено, в котором происходит дискретизация сигнала, называ- ется дискретным элементом. Дискретный характер имеют релейные, импульсные и цифро- вые сигналы. Релейные системы оперируют с сигналами, квантованными по амплитуде. Например, релейное управление может быть реали- зовано с помощью двухпозиционного реле в соответствии с выра- жением u (t) = Um sign éëe(t )ûù, где Um – амплитуда управляющего воздействия;
sign éëe(t)ûù – знаковая функция текущей ошибки e(t ) управления,
В импульсных системах имеются сигналы, квантованные по времени (амплитудно-импульсные, широтно-импульсные, частот- но-импульсные, фазоимпульсные и др.). Период T квантования сигналов в таких системах, как правило, постоянный. Например, широтно-импульсное нереверсивное управление можно предста- вить в виде
где
l éëe(t)ùû u (t) = Um l éëe(t )ùû , – скважность управления как некоторая функция текущей ошибки управления, т.е. отношение времени t у генерации управляющего воздействия с амплитудой Um к периоду T t y (t )
Цифровые системы управления оперируют с сигналами, квантованными по времени и по амплитуде и представленными в виде цифровых кодов. Квантование непрерывного сигнала по времени реализуется с помощью импульсного модулятора, а квантование по амплитуде – с помощью амплитудного квантователя (рис. 9.2).
Квантователь
Импульсный модулятор Амплитудный квантователь
Рис. 9.2. Квантование непрерывных сигналов в цифровых САУ
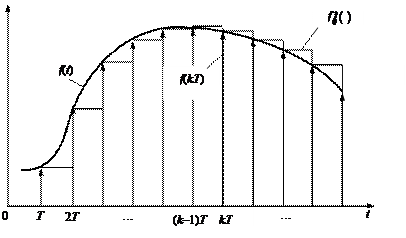
В соответствии с теоремой Котельникова – Шеннона им- пульсный модулятор должен обеспечивать дискретизацию непре- рывного сигнала по времени с частотой, по крайней мере в 2 раза превышающей максимальную частоту изменения непрерывного сигнала. В любом случае частота квантования по времени должна быть выбрана такой, чтобы обеспечить наилучшее восстановление непрерывного сигнала (исходных данных) на интервале времени kT £ t £ (k + 1) T по дискретным выборкам в k -е моменты времени, где k – номер такта квантования, T – период квантования. Таким образом, процесс восстановления непрерывного сигна- ла может рассматриваться как процесс экстраполяции. Функция f (t) на интервале T может быть представлена в виде ряда Тейлора: f (t) = f (kT) + f ¢(kT)(t - kT) + f ¢ ¢ (kT) (t - kT)2 + ..., 2!
(9.1) где f ¢(kT ), f ¢ (kT) – оценки производных в момент времени t = kT, f ¢(kT) = 1 éë f (kT) - f ((k -1) T)ùû;
= 1 é f (kT) - 2 f ((k -1) T) + f ((k - 2) T)ù; T 2 ë û …. Таким образом, для повышения точности экстраполяции сиг- нала требуется либо использовать информацию о выборках в про- шедшие моменты времени, либо повышать частоту квантования по времени. Поскольку временное запаздывание оказывает неблаго- приятное влияние на устойчивость систем управления с обратной связью, на практике обычно идут по второму пути, ограничиваясь удержанием лишь первого члена разложения ряда (9.1), т.е. на ин- тервале T принимают f (t) = f (kT). Импульсный модулятор, в котором удерживается лишь член f (kT), содержит два элемента (см. рис. 9.2) – квантователь непре- рывного сигнала по времени с периодом T и фиксатор Ф нулевого порядка (экстраполятор нулевого порядка). Квантователь можно рассматривать как идеальный ключ, замыкающийся на бесконечно короткое время через каждый такт T. Тогда выходной сигнал кван- тователя будет представлять собой функцию ¥ f * (t) = å f (kT )d(t - kT), k =0 (9.2) где f (kT ) – значение входного непрерывного сигнала в момент времени kT замыкания ключа, k = 0…∞; d(t - kT) – единичная им- пульсная функция (δ-функция), генерируемая в момент времени k замыкания ключа. Фиксатор сохраняет неизменным значение сигнала f (kT) в течение периода T квантования. Передаточная функция фиксато- ра, реагирующего на импульсные воздействия вида (9.2), находит- ся по формуле
f * (p) f * (p) 1- e - Tp
p
Реакция импульсного модулятора (квантователя и фиксатора) на некоторое непрерывное воздействие f (t) приведена на рис. 9.3. Вертикальными стрелками обозначена реакция (решетчатая функ- ция) собственно квантователя, реализующего процесс дискретиза- ции по времени. Рис. 9.3. Реакция импульсного модулятора на непрерывное воздействие f (t) В схемотехническом плане функции квантователя и экстра- полятора (фиксатора) нулевого порядка реализуют с помощью устройства выборки-хранения (УВХ) [10]. Амплитудный квантователь обеспечивает квантование вход- ного сигнала f * (t ) по уровню и выполняется на основе аналого-
Анализ и синтез импульсных систем осуществляют, как пра- вило, с применением метода Z -преобразования или разностных уравнений. Преобразование Лапласа квантованного по времени сигнала имеет вид ¥ F * (p) = å f (kT ) e - kTp . k =0 (9.3) Сделаем замену z = eTp, что позволит получить Z -преобра- зование вида ¥ F * (z) = å f (kT) z - k , k =0
где z – комплексная переменная, действительная и мнимая части которой определяются как Re(z) = eT s cos(w T ), Im(z) = eT s sin(w T ), где s+ j w = p. Анализ проекций комплексной переменной z на оси Re(z) и Im(z) позволяет сделать вывод, что область устойчивости дис- кретной САУ на комплексной плоскости ограничена окружностью единичного радиуса. Физический смысл сомножителя z–k при функции f (kT) – фик- сация и запоминание в ячейках памяти ЭВМ ее текущего (k = 0) и предшествующих значений (k = 1, 2, …).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.42 (0.013 с.) |

 w d w = -
w d w = -
 + M ) 2e
+ M ) 2e K = U рп
K = U рп
 рп D U K Dj K K w
рп D U K Dj K K w

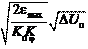 U = K
U = K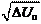 = K ¢ ,
= K ¢ ,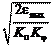 гулятора положения, K р¢п = K c .
гулятора положения, K р¢п = K c . 4 T K K
4 T K K
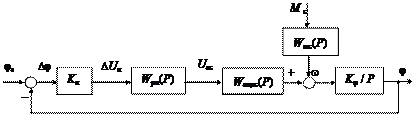
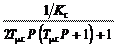 Пусть ЗКРС настроен на ТО, т.е. применен П-регулятор ско- рости, а следовательно,
Пусть ЗКРС настроен на ТО, т.е. применен П-регулятор ско- рости, а следовательно,
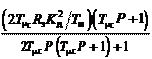 Введем обозначения:
Введем обозначения: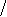
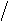 K = 1 K; K = 2 Т R K 2 Т;
K = 1 K; K = 2 Т R K 2 Т;

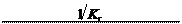 mc ë mc mc û
mc ë mc mc û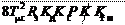
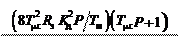 Полагая U зс = 0 и принимая во внимание, что M c = i c / K д, по- лучим
Полагая U зс = 0 и принимая во внимание, что M c = i c / K д, по- лучим P А (Р)
P А (Р) Поскольку j(P) = jз(P) – Dj(P), предыдущее выражение можно переписать относительно ошибки Dj(P):
Поскольку j(P) = jз(P) – Dj(P), предыдущее выражение можно переписать относительно ошибки Dj(P): А (Р) Р + K K K K
А (Р) Р + K K K K K K K K
K K K K K K K
K K K
 Djуст Djуст
Djуст Djуст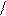 D w = 1 4 T mп.
D w = 1 4 T mп.

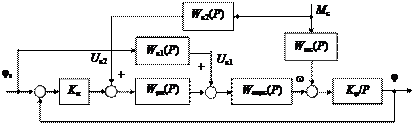

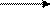

 управления, l éëe(t)ùû = T .
управления, l éëe(t)ùû = T .
 T
T