
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические погрешности средств измеренийСодержание книги
Поиск на нашем сайте Все выше сказанное про погрешности СИ относилось к статическим погрешностям. Динамические погрешности СИ возникают при измерении величин, изменяющихся во времени. Различают два вида динамических погрешностей: динамические погрешности первого рода и динамические погрешности второго рода. Динамические погрешности первого рода — обусловлены переходными процессами, связанными с инерционностью отдельных элементов прибора или, в общем случае, превращением одних видов энергии в другие. Если динамическую погрешность привести к входу прибора, то
В случае неидеальной развертки это приводит к потере информации о моменте равенства сигнала развертки и измеряемого сигнала. Динамические погрешности первого рода присущи большинству СИ. Поэтому рассмотрим их более подробно. В идеальных статических СИ при отсутствии погрешностей связь между сигналом на выходе и сигналом на входе СИ (математическая модель СИ) дается простым алгебраическим уравнением Однако, если учесть инерционные свойства СИ, его математическая модель оказывается гораздо сложнее. В этом случае значение сигнала на выходе СИ зависит не только от его значения на входе, но и от характера зависимости этого сигнала от времени. В случае аналоговых СИ математическую связь сигналов y и x можно представить в виде дифференциального уравнения. С точки зрения возможности максимальной точности анализа, конструкция СИ должна быть такой, чтобы соответствующее дифференциальное уравнение было обыкновенным линейным. В противном случае этот анализ СИ становится весьма сложным. Рассмотрим СИ, математическая модель которого дается обыкновенным дифференциальным уравнением. Это уравнение запишем в виде
Здесь y (t) – сигнал на выходе СИ. Коэффициенты a n a n-1,…определяются конструкцией СИ. Решение этого уравнения зависит от вида сигнала x (t), от начальных условий (значений производных Поскольку вид сигналов на входе СИ может самым разнообразным, желательно получить такие динамические характеристики СИ, которые не зависят от формы сигнала x (t). Кроме того, желательно иметь и стандартный вид математических моделей СИ, чтобы было их удобно сравнивать между собой. Поэтому при анализе динамических свойств СИ рассматривают так называемые стандартные сигналы. Они имеют вид: x (t) – гармоническая функция ( x (t) – единичная ступенчатая функция (функция Хевисайда, которую обозначают как 1(t)); x (t) – импульсная функция (дельта-функция Дирака d(t)). В первом случае динамической характеристикой СИ является комплексная частотная характеристика Н (w); во – втором – переходная характеристика h (t); в третьем – весовая характеристика w(t). Кроме того, математические модели СИ сводят к так называемым динамическим звеньям. Звено нулевого порядка: связь между y (t) и x (t) описывается алгебраическим уравнением вида Звено первого порядка: связь между y (t) и x (t) описывается линейным дифференциальным уравнением первого порядка. Звено второго порядка: связь между y (t) и x (t) описывается линейным дифференциальным уравнением второго порядка. В данном случае реакция звена на сигнал (или влияние звена на сигнал) существенно зависит от интенсивности диссипации энергии (трения) в этом звене. В связи с эти различают колебательное звено второго порядка и апериодическое звено второго порядка. Звенья более высокого порядка в теории измерений, как правило, не рассматривают. В случаях, когда динамические свойства СИ являются более сложными, стараются представить СИ как совокупность указанных выше простых звеньев. Таким образом, как правило, при анализе динамических свойств СИ рассматривают три вида звеньев и три вида стандартных сигналов. Существует строгая математическая связь между указанными выше динамическими характеристиками СИ, и каждая из них может быть выражена через другую.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.008 с.) |

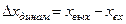 . Анализ динамических погрешностей первого рода сводится к анализу колебательных процессов в СИ, возникающих под действием измеряемого сигала.
. Анализ динамических погрешностей первого рода сводится к анализу колебательных процессов в СИ, возникающих под действием измеряемого сигала.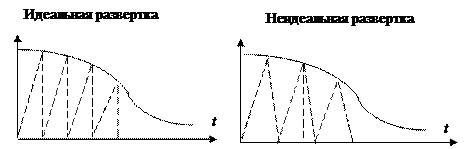 Динамические погрешности второго рода — характерны для цифровых приборов и связанны с дискретным характером измерительного преобразования. Например, в приборах с развертывающим уравновешиванием результат измерения относится или к началу, или к концу измерительного интервала (см. рис.).
Динамические погрешности второго рода — характерны для цифровых приборов и связанны с дискретным характером измерительного преобразования. Например, в приборах с развертывающим уравновешиванием результат измерения относится или к началу, или к концу измерительного интервала (см. рис.).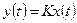 , где К =const.
, где К =const.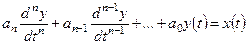 .
. ) в момент появления сигнала, т.е. состояния СИ, и, естественно, от значений коэффициентов a n a n-1,…., которые определяются конструкцией СИ.
) в момент появления сигнала, т.е. состояния СИ, и, естественно, от значений коэффициентов a n a n-1,…., которые определяются конструкцией СИ.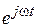 );
);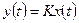 , т.е. имеет вид статической характеристики, рассмотренной выше.
, т.е. имеет вид статической характеристики, рассмотренной выше. На рис. показаны стандартные сигналы на входе и выходе СИ, динамические свойства которого могут быть представлены колебательным звеном второго порядка. Выбор вида динамической характеристики СИ зависит от вида проводимого измерения, и пристрастия инженера. Например, если процесс измерения связан с измерением периодического сигнала, с модуляцией сигнала или с использованием частотных фильтров, то удобнее использовать частотную характеристику Н (w). В этом случае влияние динамических свойств СИ и, соответственно, его динамическая погрешность сводятся к изменению амплитуды и фазы сигнала на выходе СИ по сравнению с этими параметрами сигнала на его входе (см первый рис.). В случае периодического сигнала сложной формы динамическая погрешность СИ приведет к искажению формы сигнала. При отсутствии динамической погрешности меняется только амплитуда сигнала, причем независимо от его частоты или формы.
На рис. показаны стандартные сигналы на входе и выходе СИ, динамические свойства которого могут быть представлены колебательным звеном второго порядка. Выбор вида динамической характеристики СИ зависит от вида проводимого измерения, и пристрастия инженера. Например, если процесс измерения связан с измерением периодического сигнала, с модуляцией сигнала или с использованием частотных фильтров, то удобнее использовать частотную характеристику Н (w). В этом случае влияние динамических свойств СИ и, соответственно, его динамическая погрешность сводятся к изменению амплитуды и фазы сигнала на выходе СИ по сравнению с этими параметрами сигнала на его входе (см первый рис.). В случае периодического сигнала сложной формы динамическая погрешность СИ приведет к искажению формы сигнала. При отсутствии динамической погрешности меняется только амплитуда сигнала, причем независимо от его частоты или формы.


