
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра информационно – измерительной техники и технологийСодержание книги
Поиск на нашем сайте
БНТУ Кафедра информационно – измерительной техники и технологий И. З. Джилавдари
(содержание курса лекций) Минск 2003 Оглавление Часть 1 Введение. 2 Классификация физических величин. 2 Размер физических величин. “Истинное значение” физических величин. 2 Основной постулат и аксиома теории измерений. 2 Теоретические модели материальных объектов, явлений и процессов. 2 Физические модели. 2 Математические модели. 2 Погрешности теоретических моделей. 2 Общая характеристика понятия “измерение” (сведения из метрологии) 2 Классификация измерений. 2 Измерение как физический процесс. 2 Методы измерений как методы сравнения с мерой. 2 1. Методы прямого сравнения. 2 1.1. Метод непосредственной оценки. 2 1.2. Метод прямого преобразования. 2 1.3. Метод замещения. 2 2. Методы масштабного преобразования. 2 2.1. Метод шунтирования. 2 2.2. Метод следящего уравновешивания. 2 2.3. Мостовой метод. 2 3. Разностный метод. 2 3.1. Нулевые методы.. 2 4. Метод развёртывающей компенсации. 2 Часть2 Измерительные преобразования физических величин. 2 Классификация измерительных преобразователей. 2 Статические характеристики и статические погрешности СИ.. 2 Характеристики воздействия (влияния) окружающей среды и объектов на СИ.. 2 Полосы и интервалы неопределённости чувствительности СИ.. 2 СИ с аддитивной погрешностью (погрешность нуля) 2 СИ с мультипликативной погрешностью.. 2 СИ с аддитивной и мультипликативной погрешностями. 2 Измерение больших величин. 2 Формулы статических погрешностей средств измерений. 2 Полный и рабочий диапазоны средств измерений. 2 Динамические погрешности средств измерений. 2 Динамическая погрешность интегрирующего звена. 2 Причины аддитивных погрешностей СИ.. 2 Влияние сухого трения на подвижные элементы СИ.. 2 Конструкция СИ.. 2 Контактная разность потенциалов и термоэлектричество. 2 Контактная разность потенциалов. 2 Термоэлектрический ток. 2 Помехи, возникающие из-за плохого заземления. 2 Причины мультипликативных погрешностей СИ.. 2 “Старение” и нестабильность параметров СИ.. 2 Нелинейность функции преобразования. 2 Геометрическая нелинейность. 2 Физическая нелинейность. 2 Токи утечки. 2 Меры активной и пассивной защиты.. 2 Часть 3 Физика случайных процессов, определяющих минимальную погрешность измерений 2 Возможности органов зрения человека. 2 Естественные пределы измерений. 2 Соотношения неопределенности Гейзенберга. 2 Естественная спектральная ширина линий излучения. 2 Абсолютная граница точности измерения интенсивности и фазы электромагнитных сигналов 2 Фотонный шум когерентного излучения. 2 Эквивалентная шумовая температура излучения. 2 Электрические помехи, флуктуации и шумы.. 2 Физика внутренних неравновесных электрических шумов. 2 Дробовой шум.. 2 Шум генерации - рекомбинации. 2 1/ f -шум и его универсальность. 2 Импульсный шум.. 2 Физика внутренних равновесных шумов. 2 Статистическая модель тепловых флуктуаций в равновесных системах. 2 Математическая модель флуктуаций. 2 Простейшая физическая модель равновесных флуктуаций. 2 Основная формула расчета дисперсии флуктуации. 2 Влияние флуктуаций на порог чувствительности приборов. 2 Примеры расчета тепловых флуктуаций механических величин. 2 Скорость свободного тела. 2 Колебания математического маятника. 2 Повороты упруго подвешенного зеркальца. 2 Смещения пружинных весов. 2 Тепловые флуктуации в электрическом колебательном контуре. 2 Корреляционная функция и спектральная плотность мощности шума. 2 флуктуационно-диссипационная теорема. 2 Формулы Найквиста. 2 Спектральная плотность флуктуации напряжения и тока в колебательном контуре. 2 Эквивалентная температура нетепловых шумов. 2 Часть 4 Внешние электромагнитные шумы и помехи и методы их уменьшения. 2 Емкостная связь (емкостная наводка помехи) 2 Индуктивная связь (индуктивная наводка помехи) 2 Экранирование проводников от магнитных полей. 2 Особенности проводящего экрана без тока. 2 Особенности проводящего экрана с током.. 2 Магнитная связь между экрана с током и заключенным в него проводником.. 2 Использование проводящего экрана с током в качестве сигнального проводника. 2 Защита пространства от излучения проводника с током.. 2 Анализ различных схем защиты сигнальной цепи путем экранирования. 2 Сравнение коаксиального кабеля и экранированной витой пары.. 2 Особенности экрана в виде оплетки. 2 Влияние неоднородности тока в экране. 2 Избирательное экранирование. 2 Подавление шумов в сигнальной цепи методом ее симметрирования. 2 Дополнительные методы шумоподавления. 2 Развязка по питанию.. 2 Развязывающие фильтры.. 2 Защита от излучения высокочастотных шумящих элементов и схем.. 2 Шумы цифровых схем.. 2 Выводы.. 2 Часть 5 Применение экранов из тонколистовых металлов. 2 Ближнее и дальнее электромагнитное поле. 2 Эффективность экранирования. 2 Полное характеристическое сопротивление и сопротивление экрана. 2 Потери на поглощение. 2 Потери на отражение. 2 Суммарные потери на поглощение и отражение для магнитного поля. 2 Влияние отверстий на эффективность экранирования. 2 Влияние щелей и отверстий. 2 Использование волновода на частоте ниже частоты среза. 2 Влияние круглых отверстий. 2 Использование проводящих прокладок для уменьшения излучения в зазорах. 2 Выводы.. 2 Шумовые характеристики контактов и их защита. 2 Тлеющий разряд. 2 Дуговой разряд. 2 Сравнение цепей переменного и постоянного тока. 2 Материал контактов. 2 Индуктивные нагрузки. 2 Принципы защиты контактов. 2 Подавление переходных процессов при индуктивных нагрузках. 2 Цепи защиты контактов при индуктивных нагрузках. 2 Цепь с емкостью.. 2 Цепь с емкостью и резистором.. 2 Цепь с емкостью, резистором и диодом.. 2 Защита контактов при резистивной нагрузке. 2 Рекомендации по выбору цепей защиты контактов. 2 Паспортные данные на контакты.. 2 Выводы.. 2 Часть 6 Общие методы повышения точности измерений. 2 Метод согласования измерительных преобразователей. 2 Идеальный генератор тока и идеальный генератор напряжения. 2 Согласование сопротивлений генераторных ИП.. 2 Согласование сопротивлений параметрических преобразователей. 2 Принципиальное различие информационных и энергетических цепей. 2 Использование согласующих трансформаторов. 2 Метод отрицательной обратной связи. 2 Метод уменьшения ширины полосы пропускания. 2 Эквивалентная полоса частот пропускания шумов. 2 Метод усреднения (накопления) сигнала. 2 Метод фильтрации сигнала и шума. 2 Проблемы создания оптимального фильтра. 2 Метод переноса спектра полезного сигнала. 2 Метод фазового детектирования. 2 Метод синхронного детектирования. 2 Погрешность интегрирования шумов с помощью RC - цепочки. 2 Метод модуляции коэффициента преобразования СИ.. 2 Применение модуляции сигнала для увеличения его помехозащищенности. 2 Метод дифференциального включения двух ИП.. 2 Метод коррекции элементов СИ.. 2 Методы уменьшения влияния окружающей среды и условий изменения. 2 Организация измерений. 2
Часть 1 Введение Физические основы измерений (ФОИ) – это предмет, в котором изучают общие принципы и методы измерений физических величин, основанные на конкретных физических явлениях и законах, а также изучают источники погрешностей измерений и методы повышения точности измерений. Физических величин, которые приходиться измерять в быту и производстве несколько тысяч, для каждой из них разрабатываются и используются (и не один) метод измерений и свое (СИ). Учебный курс ФОИ отличается от курса метрологии. Метрология – учение о мерах, методах и средствах обеспечения единства измерений в рамках требуемой точности. Метрология делится на законодательную и научную. Научная метрология занимается разработкой мер, методов и средств обеспечения единства измерений в рамках требуемой точности. Образно можно сказать, что научная метрология – это философия измерений. Законодательная метрология – это своеобразный “юридический кодекс” в области измерений. Законодательная метрология следит за строгим соблюдением методов, методик и правил, обеспечивающих единство измерений в рамках требуемой точности. Примеры классификации. 1. По качественным физическим свойствам: инерционность (масса); степень “нагретости” (температура); взаимодействие с постоянным электрическим полем (диэлектрическая проницаемость); и так далее. Таким образом, можно ввести электрические, механические, оптические, акустические и другие величины. 2. По зависимости величины от направления в данной точке пространства. Эту зависимость описывают три вида физических величин: - скаляры (температура, давление, масса, плотность). Их значение не зависит от направления; - векторы (скорость, сила, напряженность электрического и магнитного полей, импульс). Значения этих величин не равны нулю только в определенном направлении; Сюда же относятся и квазивекторы. В данном случае вектор, описывающий данную физическую величину, расположен вдоль выбранной оси и его направление вдоль этой оси зависит от соглашения. Например, направление вектора, являющегося результатом векторного произведения двух обычных векторов, выбирается обычно по правилу правого винта (в частности, так выбирается направление момента силы - тензоры. В данном случае значение физической величины в данной точке пространства зависит от направления. В разных направлениях значение физической величины разное. Рассмотрим это свойство тензоров подробнее на примере соотношения между векторами
Когда между обкладками конденсатора расположено кристаллическое вещество вектор Существуют также физические величины, свойства которых описываются тензорами третьего, четвертого и более высокого ранга. Скаляры можно назвать тензорами нулевого ранга, векторы – тензорами первого ранга. 3. По отношению к процессу измерения: - активные и пассивные; - аддитивные и интенсивные. Активные – величины, которые могут быть преобразованы в сигналы измерительной информации без вспомогательных источников энергии (например: ЭДС, сила тяжести и т.д.). Пассивные – величины, которые при измерении требуют использования источника энергии и преобразования в активные величины (например: сопротивление, индуктивность, емкость и т.д.). Аддитивные – величины, к которым применимы операции суммирования и вычитания (например: масса, длина, ЭДС, заряд и т.д.). Интенсивные (неаддитивные) – величины, к которым не применимы операции суммирования и вычитания (например: температура, удельная электропроводность, диэлектрическая проницаемость и т.д.). Физические модели Физика как наука о природе, изучающая простейшие, и вместе с тем, наиболее общие свойства материального мира, также базируется на теоретических моделях. Эти модели характеризуются определёнными понятиями и параметрами, которые называют физическими величинами. Примеры физических понятий и величин: пространство, система отсчета, скорость, электрическое поле, влажность, время, импульс, температура. При построении физической модели необходимо в системе материальных объектов выделить и описать физические тела, поля, условия движений, взаимодействий, ввести понятия характеризующие свойства объектов, и указать или сформулировать физические законы, описывающие связь между этими понятиями и взаимодействия между этими объектами. В соответствии с этим при построении физической модели можно выделить 3 этапа: Этап 1. Моделирование поля и вещества. Примеры: - тело – материальная точка; - тело - абсолютно твёрдое; - тело - идеально упругое. - магнитное поле – однородное; - электрическое поле – центрально симметричное; - жидкость, текущая в трубе, – не сжимаемая и не имеет вязкости; - газ в цилиндре – идеальный. Этап 2. Моделирование условий движения и взаимодействий в рамках моделей поля и вещества. Примеры: - движение происходит в инерционной системе отсчета; - трение отсутствует; - тело движется прямолинейно и равноускоренно; - деформации тела – линейно упругие. Этап 3. Формулировка физических законов, описывающих состояние, движение и взаимодействие объектов, входящих в рассматриваемую физическую систему. Примеры: - движение тел подчиняется второму закону Ньютона; - взаимодействие материальных точек подчиняется закону Всемирного тяготения; - деформация тела подчиняется закону Гука; - сила, действующая на движущиеся заряды, описывается законом Лоренца. Таким образом, физическими моделями объекта или процесса будем называть теоретические модели, включающие в себя модели вещества и поля, а также закономерности условий движения и взаимодействий. Математические модели Построенные выше физические модели необходимо описать с помощью символов в виде математических формул и уравнений. Эти символы – параметры объектов (они же обозначают физические величины) – связаны между собой в виде выше сформулированных физических законов. Совокупность формул и уравнений, устанавливающих связь между этими параметрами (физическими величинами) на основе законов физики и полученных в рамках выбранных физических моделей, будем называть математической моделью объекта или процесса. Следовательно, о физических величинах можно говорить как о параметрах, характеризующих и качественно, и количественно построенные физические модели. Процесс создания математической модели можно также разделить на 3 этапа: Этап 1. Составление формул и уравнений, описывающих состояние, движение и взаимодействия объектов в рамках выбранных физических моделей. Этап 2. Решение и исследование сугубо математических задач сформулированных на первом этапе. Основным вопросом здесь является решение так называемой прямой задачи, т.е. получение теоретических следствий и численных данных. На этом этапе важную роль играет математический аппарат и вычислительная техника (компьютер). Этап 3. Выяснение того, согласуются ли результаты анализа и вычислений с результатами измерений в пределах точности последних. Отклонение результатов расчётов от результатов измерений свидетельствует: - либо о неправильности применённых математических методов; - либо о неверности принятой физической модели; - либо о неверности процедуры измерений. Выяснение источников ошибок требует большого искусства и высокой квалификации исследователя. Бывает, что при построении математической модели некоторые её характеристики или связи между параметрами остаются неопределёнными вследствие ограниченности наших знаний о физических свойствах объекта. Например: иногда оказывается, что число уравнений, описывающих свойства объекта и связи между объектами, меньше числа параметров (физических величин), характеризующих объект. В этих случаях приходится вводить дополнительные уравнения, характеризующие объект и его свойства, иногда даже пытаются угадать эти свойства, для того, чтобы задача была решена, а результаты соответствовали результатам опытов в пределах заданной погрешности. Подобного образа задачи называются обратными. Классификация измерений Целесообразность классификации измерений обусловлена удобством разработки методов измерений и обработки результатов измерений. Измерения различаются: По способу нахождения числовых значений физических величин: - прямые; - косвенные; - совместные – косвенные измерения, при которых значение физической величины находят путем измерения физических величин различной физической природы. Пример: при измерении силы используют формулу - совокупные – косвенные измерения, при которых значение физической величины находят путём нескольких измерений других однородных физических величин. Пример: для измерения объема параллелепипеда используют формулу V = abc и проводят измерения его сторон. По характеру точности результатов единичных измерений при проведении многократных измерений: - равноточные – измерения физических величин, выполненные одинаковыми по точности средствами измерений в одинаковых условиях; - неравноточные. По виду физических величин, измеряемых при прямых измерениях для получения результата косвенных измерений: - абсолютные – измерения, основанные на прямых измерениях основных (в системе СИ) величин и на использовании значений физических констант; - относительные – измерение отношения физической величины к одноименной. При относительных измерениях широко используется внесистемная безразмерная единица измерения – децибел. Пример. При сравнении амплитуд U 1 и U 2 напряжений их отношение будет выражено в децибеллах, если его записать в виде Отношение мощностей W 1 и W 2 выражается в децибеллах, если его записать в виде В акустике децибелл – это одна из основных единиц, выражающих уровень звукового давления Р: 1дБ – уровень звукового давления, для которого По характеру зависимости измеряемой физической величины от времени: - статические – измерения физических величин постоянных во времени; - динамические – измерения физических величин изменяющихся со временем; - квазистатические – измерения физических величин изменяющихся со временем, но которые можно считать постоянными за время измерения. Отметим, что существуют более точные критерии квазистатических измерений, которые связаны с реакцией СИ на изменение измеряемой физической величины. Они будут рассмотрены ниже. По условиям определения точности результатов: - метрологические – измерения, проводимые с помощью эталонов, образцовых средств, с целью воспроизведения единиц физических величин для передачи их размеров рабочим средствам измерения; - технические – измерения, проводимые с помощью рабочих средств. Методы прямого сравнения С мерой сравнивается вся физическая величина или величина ей пропорциональная. При этом мера «заложена» в измерительный прибор, чаще всего в виде шкалы. Функциональная блок-схема метода
Существует несколько реализаций данного метода: Метод замещения Это – метод прямого преобразования, который выполняется в 2 этапа. Пример. Взвешивание груза. На этапе 1 груз подвешивается к пружине и делается отметка на стойке.
2. Методы масштабного преобразования В данном методе измерение происходит с усилением (умножением) или с ослаблением делением измеряемой величины или сигнала в процессе прямого преобразования. Здесь можно выделить несколько характерных реализаций: Метод шунтирования Пример. Измерение тока в участке цепи с помощью шунтированного амперметра. Показания амперметра I A связаны с измеряемым током IХ соотношением
Коэффициент преобразования прямой цепи К обычно называют коэффициентом усиления; коэффициент обратного преобразователя обычно обозначают через b. Из функциональной блок-схемы следует: I=К ×Δ х, х оп=β× I, Δ х = х - х оп. Отсюда найдем Эта схема может использоваться для измерения постоянных и переменных сигналов, измерения электрических и неэлектрических величин неэлектрическими методами. Мера в этой схеме находится в измерительном приборе (измерительная шкала). Пример. Простейший пример реализации – измерение напряжения с помощью усилителя постоянного тока (УПТ). В этой схеме значение сопротивления R ос соответствует коэффициенту обратной связи b. Коэффициент усиления K усилителя соответствует коэффициенту преобразования прямой цепи.
Мостовой метод Этот метод широко используется для измерения пассивных физических величин (объектов параметрического вида: сопротивление, индуктивность, ёмкость и т.д.), а также в системах регулирования. В этом методе изменение измеряемой ФВ преобразуется в изменение электрического сопротивления Rx, которое и измеряют в данном методе. Ток через измерительный прибор (см. схему) можно вычислить по формуле
Зная ток и сопротивления трех резисторов, можно найти неизвестное сопротивление. При выполнении равенства R x R 4= R 2 R 3 ток через измерительный прибор становится равным нулю. В этом случае мост считают уравновешенным. Измерительный прибор тогда становится индикатором равновесия. Если мост питается переменным напряжением и резисторы содержат реактивные элементы (емкости и индуктивности), показанные на рис., то условие равновесия моста записывается в виде ZхZ4=Z2Z3. Здесь Z – комплексное число. Поэтому условие равновесия моста сводится к выполнению двух условий: для модулей Z и для фаз: |ZX||Z4|=|Z2||Z3|, φX+φ4=φ2+φ3. Резисторы, образующие мост и имеющие сопротивление Z, могут представлять собой сложные цепи, содержащие активные и реактивные элементы, например такие: Однако, даже в случае равновесия моста, ток через измеряемый резистор не равен нулю. Погрешность данного метода зависит от погрешности, с которой известны сопротивления резисторов, а также от погрешности измерительного прибора или индикатора равновесия. Разностный метод Данный метод позволяет уменьшить сигнал на входе измерительного прибора и, тем самым, увеличить их точность за счет уменьшения мультипликативной погрешности. Это – один из наиболее точных методов. Здесь часть измеряемого сигнала компенсируется однородным сигналом, обеспечиваемого мерой.
Пример 1. Взвешивание груза. Вес груза частично компенсируется весом гири. В результате стрелка отклоняется на малый угол. Пример 2. Измерение ЭДС источника напряжения. В этой схеме микроамперметр измеряет ток, пропорциональный разности между напряжением V и напряжением на делителе, образованном резисторами R 1 и R 2, питаемыми источником опорного тока или опорного напряжения, который и
является мерой (вместе с резисторами R 1 и R 2). Нулевые методы Разностный метод называется нулевыми или компенсационным, в случае полной компенсации, т.е. если разность Δ х = х-х оп=0. Достоинством нулевых методов является то, что в ряде случаев полная компенсация измеряемого сигнала (например, тока) может осуществляться не только на входе измерительного прибора, но и в объекте измерения. В этом случае от объекта измерения не отнимается энергия, необходимая для измерения и взаимодействие СИ и ОИ практически отсутствует. Это легко видеть в рассмотренном выше примере измерения ЭДС. Если ток через микроамперметр равен нулю, тогда и ток через источник ЭДС равен нулю. В этом случае падение напряжения на внутреннем сопротивлении источника и резисторе R 2 равны нулю и вольтметр измеряет именно ЭДС источника. Примеры динамических преобразователей
В модуляционном преобразователе Ф – постоянный световой поток электрической лампочки (статический сигнал) превращается в периодический сигнал – переменный ток I. Измерение больших величин Что такое большие и малые измеряемые величины? Рассмотрим этот вопрос на примере измерения электрического сопротивления с помощью моста постоянного тока.
Условие равновесия моста в данном случае имеет вид Из (3): Очевидно Из (1) и (2) следует, что
Из (6) следует, что Учитывая, что резистор R 0 образцовый, его погрешностью Эта формула позволяет вычислить относительную погрешность измерений как больших, так и малых величин. Найдём вид полосы неопределённости. Поскольку, с учетом знаков абсолютной погрешности, сигнал на выходе нашего СИ, приведенный к входу, Поскольку абсолютная погрешность
При R x= R xмакс и R x= R xмин погрешность D R x=D R x max= R x, так что gRx=1 (или gRx=100%) и Ширина полосы неопределенности d определяется по формуле Т.к. при a <<1, где Значение Обобщим полученные результаты. Пусть в формуле (7)
Подставляя эти обозначения в формулу (7):
Конструкция СИ Ввиду большого разнообразия существующих конструкций СИ, рассмотрим данную причину аддитивной погрешности на простом примере – проволочного реостата.
 Наличие дискретного шага нам Наличие дискретного шага нам
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.014 с.) |

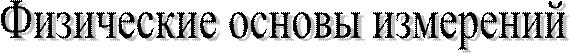
 ). Квазивектором является угловая скорость;
). Квазивектором является угловая скорость; и
и  .
. Вектор электрической индукции обычно определяется по формуле
Вектор электрической индукции обычно определяется по формуле  , где e-диэлектрическая проницаемость. Из этой формулы видно, что вектор
, где e-диэлектрическая проницаемость. Из этой формулы видно, что вектор  . В этой системе уравнений
. В этой системе уравнений  – числа, которые описывают диэлектрические свойства анизотропного вещества в выбранной системе координат xyz,
– числа, которые описывают диэлектрические свойства анизотропного вещества в выбранной системе координат xyz,  и
и  – проекции вектора
– проекции вектора  . Указанная выше система уравнений может быть записана в виде
. Указанная выше система уравнений может быть записана в виде 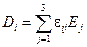 . Числа
. Числа  . Как правило, для физических величин выполняется равенство
. Как правило, для физических величин выполняется равенство 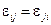 , т.е. тензор является симметричным.
, т.е. тензор является симметричным. и измеряют массу тела m и его ускорение a.
и измеряют массу тела m и его ускорение a. . Если отношение амплитуд равно 1дБ, то это означает, что отношение амплитуд
. Если отношение амплитуд равно 1дБ, то это означает, что отношение амплитуд  .
. . Если отношение мощностей (квадратов амплитуд) равно 1дБ, то
. Если отношение мощностей (квадратов амплитуд) равно 1дБ, то  .
. , где Р 0 – пороговое значение (слышимости), принимаемое равным 2×10-5 Па (Паскаль).
, где Р 0 – пороговое значение (слышимости), принимаемое равным 2×10-5 Па (Паскаль).
 На этапе 2 груз заменяют на изменяемую меру (набор гирь), пока показания не сравняются с отметкой. Основное достоинство этого метода – сводится к минимуму систематическая погрешность прибора.
На этапе 2 груз заменяют на изменяемую меру (набор гирь), пока показания не сравняются с отметкой. Основное достоинство этого метода – сводится к минимуму систематическая погрешность прибора.
 2.2. Метод следящего уравновешивания
2.2. Метод следящего уравновешивания
 Отличительной особенностью этого метода является наличие цепи отрицательной обратной связи (β - цепь), охватывающей цепь прямого преобразования (К - цепь). Благодаря этому на вход измерительного прибора поступает не весь измеряемый сигнал, а лишь его часть, пропорциональная исходному сигналу.
Отличительной особенностью этого метода является наличие цепи отрицательной обратной связи (β - цепь), охватывающей цепь прямого преобразования (К - цепь). Благодаря этому на вход измерительного прибора поступает не весь измеряемый сигнал, а лишь его часть, пропорциональная исходному сигналу. .
. Здесь I=K Δ U, Δ U = U x– IR oc. В этой схеме обычно Δ U << U x. Ток, измеряемый амперметром, пропорционален искомому напряжению:
Здесь I=K Δ U, Δ U = U x– IR oc. В этой схеме обычно Δ U << U x. Ток, измеряемый амперметром, пропорционален искомому напряжению:  .
. .
. Здесь мера формирует опорный сигнал – х оп тоже физической природы, что и сигнал х.
Здесь мера формирует опорный сигнал – х оп тоже физической природы, что и сигнал х.
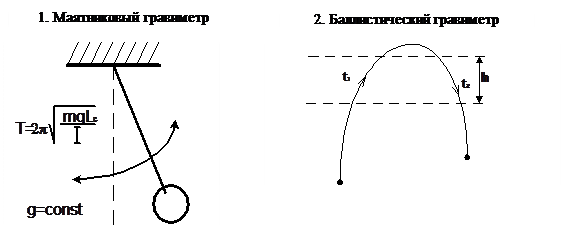
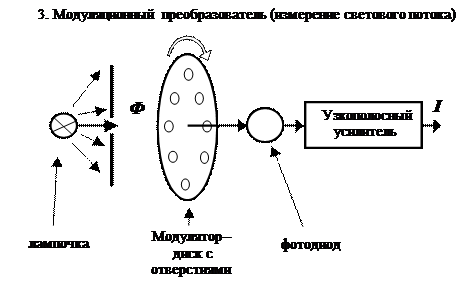 Гравиметры измеряют статическую величину – ускорение свободного падения g. В обоих примерах эта статическая величина преобразуется в сигнал, выражаемый через динамические параметры гравиметра (период колебаний в первом случае и время движения вверх-вниз тела, брошенного вверх, - во втором). В обоих случаях процессе преобразования сопровождается превращением потенциальной энергии в кинетическую и наоборот.
Гравиметры измеряют статическую величину – ускорение свободного падения g. В обоих примерах эта статическая величина преобразуется в сигнал, выражаемый через динамические параметры гравиметра (период колебаний в первом случае и время движения вверх-вниз тела, брошенного вверх, - во втором). В обоих случаях процессе преобразования сопровождается превращением потенциальной энергии в кинетическую и наоборот.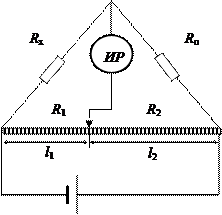 На рисунке ИР – индикатор равновесия, R 0 – образцовое сопротивление, R 1 и R 2 сопротивления плеч реохорда, l 1 и l 2 – длины плеч реохорда.
На рисунке ИР – индикатор равновесия, R 0 – образцовое сопротивление, R 1 и R 2 сопротивления плеч реохорда, l 1 и l 2 – длины плеч реохорда.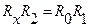 , откуда
, откуда 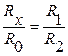 .(1). Очевидно, что
.(1). Очевидно, что 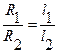 , (2), причем l 1+ l 2= L =const. (3). Из (1) и (2) следует, что
, (2), причем l 1+ l 2= L =const. (3). Из (1) и (2) следует, что  . Логарифмируя и дифференцируя это выражение, получим:
. Логарифмируя и дифференцируя это выражение, получим: 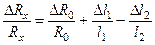 , где
, где 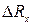 — погрешность оценки сопротивления R x,
— погрешность оценки сопротивления R x, 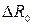 — погрешность образцового сопротивления R 0,
— погрешность образцового сопротивления R 0, 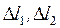 — погрешности измерения длины.
— погрешности измерения длины. , и (4), найдём:
, и (4), найдём: 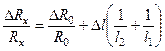 (5),
(5),  – относительная погрешность измерения.
– относительная погрешность измерения.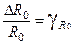 ,
,  . Можно записать (5) в виде:
. Можно записать (5) в виде: 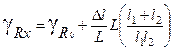 . Учитывая, что L = l 1+ l 2, после простого преобразования, получим
. Учитывая, что L = l 1+ l 2, после простого преобразования, получим 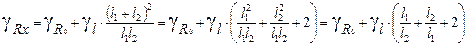 .
. , из предыдущего выражения, получим
, из предыдущего выражения, получим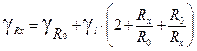 (6)
(6) как при R x®0, так и при R x®¥.
как при R x®0, так и при R x®¥. можно пренебречь. Тогда формула (6) запишется в виде
можно пренебречь. Тогда формула (6) запишется в виде 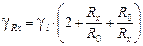 (7)
(7)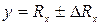 , вид полосы неопределенности определяется следующими соотношениями:
, вид полосы неопределенности определяется следующими соотношениями:  (8).
(8).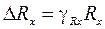 , из формулы(7), пренебрегая величиной
, из формулы(7), пренебрегая величиной 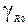 , имеем
, имеем 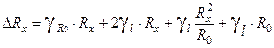 . (9). Учитывая (8), найдем максимальный и минимальный сигналы на выходе:
. (9). Учитывая (8), найдем максимальный и минимальный сигналы на выходе: 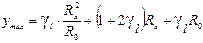 (10).
(10).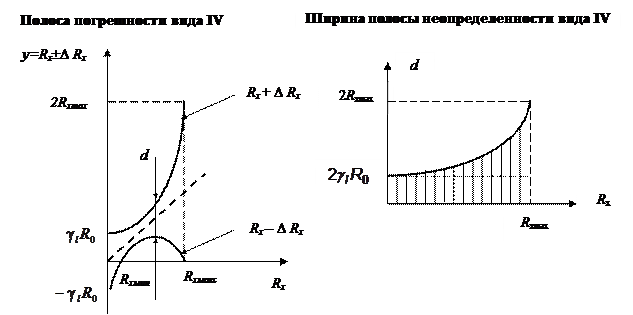 Функция
Функция  – парабола, ветви которой обращены вверх. В свою очередь,
– парабола, ветви которой обращены вверх. В свою очередь, 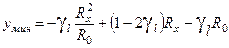 (11).Функция
(11).Функция 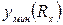 – парабола с ветвями, обращенными вниз. На графике зависимости
– парабола с ветвями, обращенными вниз. На графике зависимости 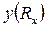 параметр d – ширина полосы неопределенности R xмакс и R xмин — максимальное и минимальное значения, которые еще могут быть измерены.
параметр d – ширина полосы неопределенности R xмакс и R xмин — максимальное и минимальное значения, которые еще могут быть измерены. .
.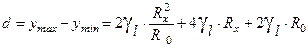 (12) Функция d (R x) – парабола. Обозначим в формуле (7)
(12) Функция d (R x) – парабола. Обозначим в формуле (7) 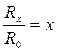 , тогда
, тогда  . Проведем анализ этой формулы. Сначала найдем минимум функции
. Проведем анализ этой формулы. Сначала найдем минимум функции 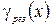 , взяв производную по х. Найдем, что при х =1
, взяв производную по х. Найдем, что при х =1 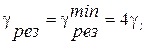 . Найдем максимально и минимально возможные значения х. Они находятся там, где
. Найдем максимально и минимально возможные значения х. Они находятся там, где 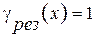 . Из этого равенства имеем
. Из этого равенства имеем  . Обычно
. Обычно  . Решая квадратное уравнение, получим
. Решая квадратное уравнение, получим 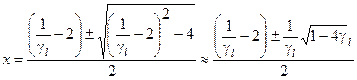 .
.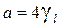 , выполняется соотношение
, выполняется соотношение  , получим:
, получим: 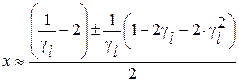 . Отсюда следует, что
. Отсюда следует, что 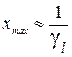 и
и  , где
, где 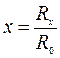 и
и 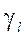 - погрешность реохорда. Отсюда легко найти минимальное и максимальное значения R x, которые можно измерить с погрешностью £100%. Таким образом, значения
- погрешность реохорда. Отсюда легко найти минимальное и максимальное значения R x, которые можно измерить с погрешностью £100%. Таким образом, значения 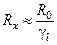 следует отнести к большим значениям, а значения
следует отнести к большим значениям, а значения 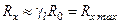 – к малым.
– к малым. – это нижний порог чувствительности данного СИ, значение
– это нижний порог чувствительности данного СИ, значение  – это верхний порог чувствительности СИ.
– это верхний порог чувствительности СИ. – любая величина, подлежащая измерению. Будим считать, что:
– любая величина, подлежащая измерению. Будим считать, что: — погрешность чувствительности,
— погрешность чувствительности,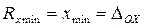 – нижний порог чувствительности,
– нижний порог чувствительности,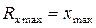 – верхний порог чувствительности,
– верхний порог чувствительности, – погрешность СИ.
– погрешность СИ.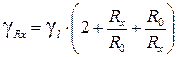 , получим универсальную формулу для расчета статических погрешностей СИ:
, получим универсальную формулу для расчета статических погрешностей СИ: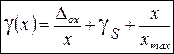 , (13), где
, (13), где  - абсолютная погрешность прибора (сдвиг нуля),
- абсолютная погрешность прибора (сдвиг нуля),  - погрешность чувствительности (погрешность наклона функции преобразования) или мультипликативная погрешность.
- погрешность чувствительности (погрешность наклона функции преобразования) или мультипликативная погрешность.



