
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная формула расчета дисперсии флуктуацииСодержание книги
Поиск на нашем сайте
Флуктуации – результат совместного действия огромного числа частиц образующих макросистему. В этом случае, в соответствии с предельной теоремой теории вероятностей, вероятность обнаружить значение величины в бесконечно малом интервале от x до x + dx – элементарная вероятность Под значением флуктуации параметра х понимают именно значение величины sх. Физический смысл этого параметра состоит в следующем: величина sх – это корень квадратный из среднего квадрата отклонения параметра х системы от его среднего значения. Отклонения параметра х от своего среднего значения в результате флуктуации могут быть сколь угодно большими по величине. В соответствии с формулой (2), чем меньше отклонение, тем чаще они происходят, и наоборот. Формулу (3) будем считать основной формулой для расчета интенсивности флуктуаций равновесной системы. Напомним, что A (х) – работа, необходимая для того, чтобы вывести систему из положения равновесия и привести ее данное состояние. Влияние флуктуаций на порог чувствительности приборов Флуктуации играют важную роль в действии современных высокочувствительных приборов – весов, гальванометров, микровольтметров и т. п. Чувствительность этих приборов столь высока, что они позволяют регистрировать явления того же масштаба, что и флуктуации, вызываемые тепловым движением молекул в самом приборе. Это влечет за собой важное следствие: при однократном измерении физической величины, значение которой меньше, чем флуктуации самого прибора, он регистрирует собственное тепловое движение (фон или шум), а не измеряемую величину. В этом смысле говорят, что тепловое движение определяет порог чувствительности данной конструкции прибора (заметим еще раз – при однократном измерении). Дальнейшее повышение чувствительности для измерения величин, лежащих ниже фона теплового движения, сопряжено с выполнением многократных измерений (или, что тоже самое, увеличение времени измерения или, в случае измерения периодических сигналов, уменьшением полосы частот, в которой производится измерение). Действительно, если прибор регистрирует только собственное движение, то среднее отклонение прибора будет равно нулю. Если же на шум накладывается некоторое внешнее воздействие, то прибор будет флуктуировать около некоторого нового положения, и его среднее отклонение будет отлично от нуля. Чем больше число произведенных измерений, т.е. чем больше время наблюдения, тем меньшие значения физической величины (лежащие ниже фона) могут быть зарегистрированы. Среднее квадратическое значение флуктуации: Примеры расчета тепловых флуктуаций механических величин Скорость свободного тела Будем рассматривать свободное твердое массой m как подсистему, находящуюся в тепловом контакте с окружающей средой, которую в таком случае называют тепловым резервуаром или термостатом. Окружающую среду практически всегда можно выбрать такой, что тело и резервуар допустимо считать замкнутой системой, имеющей температуру Т.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.41 (0.009 с.) |

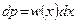 подчиняется закону Гаусса, причем
подчиняется закону Гаусса, причем  (2). Без ограничения общности, в теории флуктуаций считают, что < x> =0. Сравнивая (2) с (1), найдем
(2). Без ограничения общности, в теории флуктуаций считают, что < x> =0. Сравнивая (2) с (1), найдем  .(3)
.(3) - это и есть погрешность однократного измерения величины x. При многократном измерении мы измеряем среднее значение величины x. Но среднее значение — тоже случайная величина и погрешность среднего значения
- это и есть погрешность однократного измерения величины x. При многократном измерении мы измеряем среднее значение величины x. Но среднее значение — тоже случайная величина и погрешность среднего значения  — это среднее квадратическое значение среднего значения. Эта погрешность вычисляется по формуле
— это среднее квадратическое значение среднего значения. Эта погрешность вычисляется по формуле 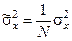 , где N – число измерений. Отсюда следует, что с увеличением числа измерений погрешность измерения среднего значения уменьшается как
, где N – число измерений. Отсюда следует, что с увеличением числа измерений погрешность измерения среднего значения уменьшается как  .
. Любое тело характеризуются импульсом р своего макроскопического движения относительно среды. В состоянии равновесия никакого макроскопического движения нет, т.е. р =0. Движение, однако, может появиться в результате флуктуации. Определим вероятность такой флуктуации. Минимальная работа, необходимая, для того, чтобы сообщить телу импульс р, равна изменению кинетической энергии тела. Поскольку в состоянии равновесия движения нет, то начальное значение кинетической энергии равно нулю. Поэтому работа внешних сил равна просто кинетической энергии тела, которую оно приобретает в результате флуктуации:
Любое тело характеризуются импульсом р своего макроскопического движения относительно среды. В состоянии равновесия никакого макроскопического движения нет, т.е. р =0. Движение, однако, может появиться в результате флуктуации. Определим вероятность такой флуктуации. Минимальная работа, необходимая, для того, чтобы сообщить телу импульс р, равна изменению кинетической энергии тела. Поскольку в состоянии равновесия движения нет, то начальное значение кинетической энергии равно нулю. Поэтому работа внешних сил равна просто кинетической энергии тела, которую оно приобретает в результате флуктуации:  , где vx – проекции скорости макроскопического движения. Отсюда и из основной формулы (3), учитывая, что в данном случае физическая величина x это проекция скорости тела vx, найдем, что флуктуация скорости тела
, где vx – проекции скорости макроскопического движения. Отсюда и из основной формулы (3), учитывая, что в данном случае физическая величина x это проекция скорости тела vx, найдем, что флуктуация скорости тела  . Причина движения (дрожания) тела – тепловое движение окружающих тело молекул среды и столкновение этих молекул с телом. Это ничто иное, как броуновское движение.
. Причина движения (дрожания) тела – тепловое движение окружающих тело молекул среды и столкновение этих молекул с телом. Это ничто иное, как броуновское движение.


