Компьютерный урок «Сравниваем фигурки наложением»

Лист определений «Сравниваем фигурки наложением»

Для того чтобы осуществить наложение фигурок на бумаге, необходимо вырезать фигурки по контуру и наложить одну на другую. При этом крайне важно вырезать фигурки точно по контуру, в противном случае результат сравнения нельзя будет считать достоверным. Понятно, что для первоклассника это достаточно сложная задача. С помощью компьютерного инструмента лапка, напротив, выполнить сравнение наложением очень легко. Прежде всего, захватить и перенести фигурку лапкой гораздо проще, чем вырезать и наложить одна на другую бумажные фигурки. Кроме того, инструмент лапка запрограммирован таким образом, чтобы максимально облегчить процедуру сравнения. Во-первых, когда мы захватываем фигурку лапкой, она становится полупрозрачной. Поэтому если фигурки неодинаковые, то при наложении мы это сразу заметим: одна из фигурок будет выходить за границы другой. Во-вторых, при наложении фигурки автоматически совмещаются по ключевым точкам. Это очень важный момент, так как самостоятельно детям было бы крайне сложно правильно наложить фигурки одну на другую: ведь можно и совершенно одинаковые фигурки наложить таким образом, что они не совпадут. Более того, если фигурки имеют нетривиальную форму, то сложно даже объяснить детям, каким образом следует накладывать их одна на другую. В компьютерном курсе эта проблема не стоит: лапка запрограммирована таким образом, что если одну фигурку поднести достаточно близко к другой, то фигурки автоматически совместятся по правильным точкам. Это означает, что если фигурки одинаковые, то они непременно совпадут, если же фигурки разные, то они совпадут насколько это возможно. Таким образом, при нашей процедуре наложения ребёнок легко может определить, одинаковые фигурки или разные. Ещё одна важная особенность лапки — эффект отпрыгивания, который состоит в следующем. Если фигурку совместить с другой фигуркой и щёлкнуть на ней лапкой, то одна из фигурок немного сдвинется в сторону (отпрыгнет) или даже вернётся на свою исходную позицию. Это сделано для того, чтобы в процессе решения задачи часть фигурок не потерялась. Фигурка может потеряться, если вы наложите друг на друга две одинаковые фигурки или если большая фигурка полностью покроет маленькую. Эффект отпрыгивания позволяет учащимся видеть все фигурки, представленные в задаче.

Решение задач

Задача 63. Решая эту совсем несложную задачу, учащиеся на практике знакомятся с инструментом лапка, учатся сравнивать фигурки наложением и перемещать фигурки в окно. Дети учатся использовать описанные выше полезные свойства лапки: прозрачность, склеивание по правильным точкам, отпрыгивание. В процессе работы над этой и последующими задачами ребёнок должен уяснить следующие важные моменты. Первый: чтобы сработал эффект автоматического совмещения, фигурку надо поднести к другой достаточно близко. Второй: не надо щёлкать мышью сразу после совмещения фигурок, иначе одна из них отпрыгнет в сторону. Прежде следует внимательно рассмотреть картинку, чтобы понять, одинаковые фигурки или нет. Только после этого можно щёлкнуть мышью, чтобы фигурка отклеилась. Если нужно положить фигурку в окно, мышью щёлкать и вовсе не надо.

Скорее всего, в классе найдутся учащиеся, которые будут сравнивать фигурки на глаз, по каким-либо причинам не желая использовать лапку. С такими детьми придётся побеседовать индивидуально, объяснив, что человеческий глаз в состоянии заметить только существенную разницу в размерах и форме фигурок, а если эта разница незначительна, то, сравнивая фигурки на глаз, моно легко ошибиться, в то время как с помощью лапки можно сравнивать такие фигурки, разница между которыми практически незаметна. И даже в этом случае лапка даст абсолютно достоверный ответ. Впрочем, впереди ещё будут задачи, в которых дети будут вынуждены использовать лапку, чтобы избежать возможных ошибок.

Задача 64. В этой задаче фигурки имеют сложную форму. Вырезать такие фигурки точно по контуру было бы сложно даже взрослому человеку, да и с наложением могли бы возникнуть трудности. На компьютере же эта задача решается очень легко. Нужно лишь захватить одну фигурку лапкой и поднести к другой так близко, чтобы сработало автоматическое совмещение. Далее следует внимательно рассмотреть наложенные фигурки. Если везде виден один внешний контур, значит, фигурки одинаковые. Если хотя бы в одном месте появляется второй внешний контур, значит, фигурки разные. Ребёнок может объяснить своё решение и другими словами, например так: если одна фигурка нигде не выходит за границы другой, значит, фигурки одинаковые. Если хотя бы в одном месте выходит фигурки разные.

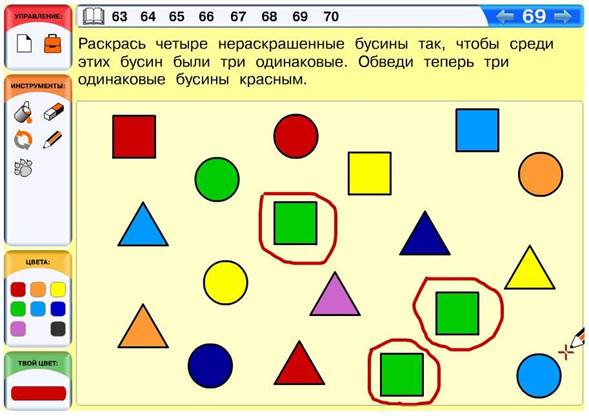
Задача 65. В этой задаче в принципе некоторые из фигурок можно было бы сравнить на глаз. Если ребёнок скажет, что он и так видит, какие фигурки одинаковые, более того, если он даже выберет и положит в окно правильные фигурки, всё равно попросите его проверить своё решение с помощью процедуры наложения.

Задача 66. Как сказано в условии задачи, сравнивать фигурки наложением здесь необязательно. Однако, если кто-то захочет искать такие же фигурки с помощью наложения (это гораздо проще, чем сравнивать визуально), препятствовать этому не следует. Ну и конечно, если учащийся ошибся в решении задачи, пусть сравнит фигурки наложением и убедится в том, что его решение неправильное.

Задача 67. Среди бусин на экране есть несколько подходящих пар, однако в результате решения задачи в окне у всех должен получиться одинаковый набор бусин: голубая треугольная, голубая квадратная, зелёная круглая, красная круглая.

Задача 68. В этом слове всего десять букв, найти одинаковые пары совсем несложно. Большинство детей, скорее всего, успешно справятся с этой задачей.

Задача 69. Эта задача отчасти напоминает компьютерные задачи 50 и 52. Хорошенько рассмотрев нераскрашенные бусины, мы убеждаемся, что среди них есть две одинаковые. Это ключ к решению задачи: теперь мы можем выбрать одну из четырёх раскрашенных квадратных бусин и раскрасить две нераскрашенные квадратные бусины тем же цветом. Как вы понимаете, решений в этой задаче много.

Вот одно из решений данной задачи:

Задача 70 (необязательная). Здесь детям придётся использовать полученные в этом уроке знания в несколько необычном контексте. До сих пор с помощью процедуры наложения мы сравнивали фигурки в целом — одинаковые они или нет. При этом нам не приходилось проводить сравнение по отдельным признакам (высоте, ширине и т. п.), хотя метод наложения, как мы уже говорили, допускает сравнение фигур как по линейным размерам, так и по площади. В этой задаче мы будем сравнивать ёлочки по высоте. Для этого после наложения фигурок мы должны сопоставлять не фигурки в целом, а только их высоту. Дополнительная сложность состоит в том, что для решения задачи недостаточно выяснить, одинаковой высоты две ёлочки или нет, — нужно определить, какая из ёлочек выше, а какая ниже. В конечном же итоге найти самую высокую и самую низкую.

Урок «Рисуем в окне»

Новое ключевое выражение: нарисуй в окне.

На этом уроке дети опять знакомятся с новым инструментальным действием «нарисуй в окне». Это действие содержательно имеет тот же смысл, что и действие «вырежи и наклей в окно», т. е., чтобы в окне появился определённый объект (или объекты). Конечно, любой объект можно вырезать и наклеить в окно, но это довольно долго. Что касается фигурок, то тут выбора у детей нет: ведь рисовать фигурки тоже долго. Кроме того, мы не будем давать задания на рисование фигурок (кроме задачи 71) ещё по одной причине. На самом деле невозможно добиться однозначного понимания правил рисования относительно каждой фигурки. В учебнике мы специально рисуем фигурки так, чтобы в любом задании можно было однозначно отличить слона от ежа, грушу от яблока и т. д. Если мы предложим детям нарисовать слона, то он может оказаться похожим на собаку, кошку или кого-нибудь ещё. При этом вы не сможете опереться ни на какие взаимные соглашения, чтобы доказать ребёнку, что его решение неверное, может, именно  так он видит слона. Таким образом, включая такие задания в курс, мы нарушаем основной принцип его построения — однозначное понимание всех учебных текстов учителем и детьми. Мы также не можем предложить детям задачу «Нарисуй в окне такую же фигурку» или «Нарисуй в окне две одинаковые фигурки», поскольку у ребёнка не хватит технических возможностей обеспечить идентичность фигурок по всем свойствам, в том числе совпадение при наложении. Совсем другой будет ситуация, если мы попросим ребёнка нарисовать в окне бусину. Во-первых, это совсем несложно даже для первоклашки; например, это проще, чем вырезать бусину и наклеить её. Во-вторых, бусины имеют лишь 2 свойства, полностью их определяющие: форму и цвет. Договорённость о цветах у нас была введена явно, о формах бусин тоже. Значит, в любой задаче вам удастся добиться с ребёнком однозначного понимания условия. Результат в этом случае не зависит от художественных способностей ребёнка, его технических возможностей. Поэтому в заданиях, где необходимо создать в окне бусину (или несколько бусин) или какую-то структуру из бусин (цепочку, мешок), мы чаще будем использовать формулировку «нарисуй в окне», хотя «вырежи и наклей в окно» в таких случаях тоже иногда будет встречаться. Если же нужно создать в окне фигурки, то мы будем всегда использовать формулировку «вырежи и наклей в окно».

Что касается правил нового действия «нарисуй в окне», то они для детей не будут новыми, — фигурка или бусина считается нарисованной в окне только в том случае, если она лежит в нём целиком, не пересекая границ (синих линий). Если в окне нарисовано несколько фигурок, они не должны перекрываться.

Решение задач из учебника

Задача 69. Данная задача кажется совсем простой, но это — первое задание совершенно нового типа. В нашем курсе дети уже достраивали объект по образцу в задачах типа «Сделай фигурку такой же — раскрась квадратики». Но здесь дети впервые создают объект по образцу совершенно самостоятельно, т. е. с нуля. Повторим, что в отличие от фигурок (где при сравнении фигурок мы учитываем абсолютно все признаки) бусины полностью характеризуются двумя признаками — формой и цветом. Поэтому если ребёнок нарисовал в окне красную бусину квадратной формы, то решение следует считать верным. То, что эта бусина немного больше той, которая дана в задаче, или расположена относительно страницы иначе, совершенно неважно. Возможно, в первых задачах бусины у детей будут получаться немного кривоватыми. Если вы видите, что ребёнок старался, то мы советуем вам не обращать на это слишком много внимания в том случае, если отчётливо можно различить форму и цвет бусины. Если квадратную бусину у ребёнка сложно отличить от круглой, то, возможно, есть смысл вернуть учащегося к листу определений «Бусины».

Задача 70. Эта задача тоже очень важная. В ней дети впервые создают объекты по описанию. Каждое описание состоит из двух условий — формы и цвета, которые задают однозначно любую бусину.

Задача 71. Несмотря на все соображения, высказанные в обсуждении данного листа определений, мы предлагаем в этой задаче детям нарисовать в окне две фигурки. Это сделано для того, чтобы у детей не сложилось впечатление, что окна предназначены только для рисования бусин и рисовать в них фигурки (или что-то ещё) нельзя в силу каких-то содержательных причин. Это, конечно, не так с точки зрения информатики вообще-то всё равно, что рисовать в окнах, наши ограничения на рисование фигурок в окнах вызваны чисто техническими причинами — нашими договорённостями о правилах игры.

Постарайтесь не подходить к выполнению этого задания слишком строго: ведь способности к рисованию у всех детей разные. Ясно, что цвета фигурок должны соблюдаться. Также должны соблюдаться общие представления о форме данных предметов: банан должен выглядеть вытянутым, а мяч — круглым.

Задача 72. Отличие данной задачи от аналогичных предыдущих состоит в том, что здесь детям предлагается найти две пары одинаковых фигурок, т. е. по сути, найти несколько решений одной и той же задачи. В математике считается, что решить задачу — значит найти все её решения (либо доказать, что их нет). Вообще умение находить несколько решений одной задачи является важным не только в математике и информатике, но и в жизни. Только перебрав все решения (или хотя бы несколько), мы сможем найти более рациональный способ достижения своей цели. Однако обучить поиску всех (или хотя бы нескольких) решений одной задачи — дело совсем не простое. В 1 классе мы начинаем эту работу пока очень осторожно, на примере таких задач, как эта.

Задача 73 (необязательная). Вы, конечно, заметили, что изредка мы предлагаем детям задачи, где ограничений в условиях совсем мало. Так, мы хотим показать детям разницу между построением объекта в системе ограничений и при их отсутствии. По сути, ограничений на решение здесь всего два — чтобы все объекты были нарисованы в окне, чтобы все они были бусинами. Конечно, такое задание можно сформулировать короче — «Нарисуй в этом окне бусины». Но мы специально подчёркиваем свободу выбора количества и видов бусин выражениями «сколько хочешь» и «каких хочешь».

Задача 74. Вполне возможно, что в левом окне одинаковые бусины будут выглядеть не совсем одинаковыми. Однако их следует считать таковыми и признавать решение ребёнка верным, если они обе синие и отчётливо видно, что они одинаковой формы.

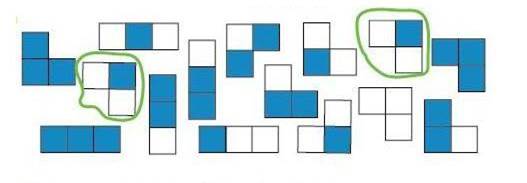
Задача 75 (необязательная). Аналогичные задачи ребятам уже встречались (см. комментарий к задаче 43 из учебника). Как и в задаче 43, здесь надо внимательно прочитать задание, выделить условия, которые должны выполняться, и затем попытаться найти пару бусин, соответствующую этим условиям. В данном случае решение можно построить как из зелёных, так и из оранжевых бусин.

Задача 76 (необязательная). Эта задача представляет собой ловушку для тех детей, которые продолжают выделять детали рисунка, а не области, как мы договорились на листе определений. Такие дети самостоятельно увидят всего 2 области — звезду и фон. В этом случае областей для раскрашивания детям просто не хватит и в решении возникнет заминка. В этот момент желательно посоветовать ребёнку вернуться к листу определений «Области». В этой картинке ровно 9 областей, и все они оказываются раскрашенными в результате выполнения задания.

Задача 77 (необязательная). Если кто-то из детей запутался, предложите ему разбить фигурки на группы по числу закрашенных клеток. Видим, что в некоторых фигурках закрашена лишь одна клетка, в других — две, в остальных — три. Значит, получается три группы по числу закрашенных клеток. Фигурок с одной закрашенной клеткой четыре, и все они разные. Следовательно, эти фигурки можно больше не рассматривать (чтобы не сбиться, их можно просто вычеркнуть). Фигурок с тремя раскрашенными клетками две, и они разные, значит, их можно тоже вычеркнуть. Теперь осталось рассмотреть группу из оставшихся фигурок и найти среди них две одинаковые.

Урок «Все, каждый»

Новые ключевые понятия: все, каждый, все остальные.

Понятие все является вторым из наиболее важных понятий математической информатики, с которыми ученики знакомятся в нашем курсе. (Первым было понятие одинаковости.)

Надеемся, что ученикам понятия все, каждый покажутся простыми. Они и на самом деле простые (например, «каждый его знает»). Однако не всегда это было так. Например, постижение силлогизмов Аристотеля составляло существенную часть средневекового высшего образования. Возможно, вы встречали и примеры силлогизмов вроде

                                    Все люди смертны.

                                    Сократ — человек.

                                _____________________________

                                    Следовательно, Сократ смертен.

Надеемся, что ученики без труда будут в будущем строить рассуждения такого рода. Но предостерегаем вас от игнорирования того, что понимание детьми таких «очевидных» слов, как, например, каждый, поначалу может немного или даже существенно отличаться от вашего.

Слова все, каждый всегда относятся к некоторой совокупности объектов. Иногда эта совокупность устроена сложно: все атомы во Вселенной или все действительные числа. Мы довольно долго будем иметь дело с простыми совокупностями, умещающимися на одной странице, где объекты сравнительно легко перебрать по одному.

Именно такой перебор (по одному) и нужно осуществлять каждый раз, когда мы выполняем какое-то действие или проверяем какое-то свойство для всех объектов. Не надо формулировать это в виде правила. Лучше, если дети будут относиться к словам все, каждый просто как к словам русского языка с очевидным смыслом. Однако желательно проверить, все ли дети (опять все!) правильно понимают этот смысл и действительно в какой-то мере систематически просматривают все объекты. Это очень важно для формирования информатического, конструктивного взгляда на понятия и процессы.

Просмотр объектов

В нашем курсе мы стараемся сделать наглядными, видимыми объекты информатики (а также математики и лингвистики), так же как и отношения между ними и действия над ними. Такая визуализация объектов информатики, сочетание образного и символического описаний очень продуктивны в обучении. Они же являются одним из основных направлений развития информационных технологий в целом и их применения в образовании в частности. Все чаще и чаще, рассказывая что-то друг другу, люди одновременно показывают это на экране, куда проецируется компьютерное изображение, где появляются все необходимые иллюстрации.

Речь пойдёт об одном важном умении: просматривать и сортировать графические или символьные объекты, расположенные в некотором поле (скажем, на странице или в поле одной задачи). В жизни такое умение необходимо везде, начиная от чтения меню, расписания движения поездов и самолётов, географических карт и заканчивая поиском подходящих туфель на полке магазина. Возможно, в предыдущих задачах некоторые ребята уже пытались осуществить просмотр объектов, однако без него можно было и обойтись. В последующих задачах полный и систематический просмотр объектов становится необходимым условием решения задачи.

Процедура просмотра, которую обычно использует ребёнок, а часто и взрослый, хаотическая. Это — беспорядочное перескакивание взгляда с одного предмета на другой. Иногда эта стратегия не так уж плоха. Однако она не годится в тех случаях, когда требуется выполнить действительно полный просмотр, или, как иногда говорят в информатике и математике, полный перебор. Поэтому необходимо вычёркивать или обводить уже просмотренный объект или хотя бы ставить на нём (или вблизи него) точку. Но если ребёнок не использует графических пометок, перечисленных выше, полезно предложить ему некоторую стратегию просмотра. (Например, просматривать объекты в ряду слева направо, переходя к следующему ряду сверху вниз.) Использование этой стратегии можно облегчить с помощью линейки, которую надо перемещать сверху вниз, каждый раз просматривая появившиеся целиком над линейкой объекты. Эта стратегия требует большой аккуратности и хорошо работает, если объекты расположены по строкам.

Через несколько лет на уроках информатики детям придётся составлять программы для компьютера, включающие полный просмотр, сортировку объектов и другие важные операции. Мы хотим, чтобы дети хорошо понимали, что это значит, и умели это делать вручную. Иначе как они смогут сознательно обучить этому компьютер?

Решение задач из учебника

Задача 78. Дети уже встречались с понятием «инструкция» в задаче 67. Но если в задаче 67 порядок выполнения действий не влиял на результат, то здесь нарушение последовательности выполнения пунктов инструкции ведёт к ошибкам и даже отказам. Например, если учащийся выполнит сначала второй пункт инструкции, а затем третий, то первый пункт он после этого выполнить просто не сможет — в наборе не останется бусин для раскрашивания. Таким образом, в этой задаче вам, возможно, придётся обсудить с кем-то из детей, что такое инструкция и как её необходимо выполнять.

Задача 79. Проследите за тем, чтобы ребёнок не забыл выполнить проверку (это последняя строчка задания), даже если он абсолютно уверен в правильности своего решения (это опять соблюдение правил игры). Проверка заключается в том, чтобы осуществить полный перебор всех оставшихся на листе вырезания фигурок и убедиться, что это не улитки.

Задача 80. Эта задача напоминает задачу 78. Однако здесь результаты выполнения отдельных заданий не связаны между собой, поэтому их можно выполнять в любом порядке и даже одновременно. Например, взять любую бусину, определить её форму, прочитать в условии, каким цветом надо раскрашивать бусины такой формы, раскрасить её этим цветом и перейти к другой бусине. Так будем делать до тех пор, пока все бусины не будут раскрашены. Это один из алгоритмов выполнения данного задания, но не самый быстрый. Дети быстрее выполнят пункты задания по порядку, тогда им не придётся постоянно возвращаться к условию задачи.

Задача 81. Обратите внимание на эту задачу: она является важной с разных точек зрения. С одной стороны, данная задача поддерживает курс арифметики — здесь детям придется вспомнить названия некоторых цифр. С другой стороны, здесь впервые дети используют инструментальное действие «соедини» не для выделения пары объектов, а для установления соответствия между двумя группами объектов. Понятие «соответствие» лежит в основе многих разделов математики, в частности теории функций. В данном случае ситуация совсем простая — нужно установить соответствие между набором цифр и набором слов (названий этих цифр). Соответствие при этом является взаимно-однозначным — каждой цифре можно сопоставить ровно одно слово и наоборот. Несмотря на глубину теоретической подоплёки данной задачи, думаем, у детей она никаких вопросов не вызовет. Поэтому, хотя задача и является для ребят совершенно новой, советуем не давать им никаких общих пояснений. Как и любая другая задача со словами «все», «каждый», эта задача должна заканчиваться проверкой, включающей полный перебор. Необходимо ещё раз просмотреть каждую цифру и проверить, что от неё идёт линия к некоторому слову. 

Задача 82. Условно говоря, мы конструируем фигурку по образцу, точнее, мы конструируем три фигурки, при этом для каждой из них образцом являются две другие. Действительно, чтобы раскрасить правильно первую фигурку, нужно посмотреть, в какие цвета раскрашены в других фигурках её пустые клеточки (фиолетовый, голубой, жёлтый). То же самое надо проделать с двумя другими фигурками. Однако стратегия решения может быть иной: можно каждую клеточку анализировать только один раз — сразу в трёх фигурках. Последний способ более эффективен.

Задача 83. В задачеиспользуются буквы латинского алфавита, правда, в витиевато-декоративном начертании. Здесь ребята оценивают одинаковость латинских букв как фигурок.

Задача 84 (необязательная). Как видите, здесь нужно создать набор объектов (бусин) по описанию, которое содержит отрицание («чтобы не было двух одинаковых бусин»). Конечно, чтобы выполнить это задание, совсем необязательно анализировать и понимать утверждение на уровне формальной логики. Эту задачу можно решать методом проб и ошибок, т. е. для начала просто наобум. Нарисуем 8 нераскрашенных круглых бусин. Раскрасим две бусины разными цветами: ведь если мы раскрасим их одинаковым цветом, то у нас сразу появятся две одинаковые бусины. Теперь раскрасим третью бусину так, чтобы она не была ни такой, как первая, ни такой, как вторая. Для этого её надо раскрасить цветом, отличным от цвета первой и второй бусин. Так можно раскрашивать бусины и дальше, проверяя на каждом шаге, не появилось ли в наборе двух одинаковых раскрашенных бусин.

Задача 85 (необязательная). В этой задаче детям необходимо помнить, что зеркально симметричные фигурки являются разными.

Вот решение данной задачи:

Задача 86 (необязательная). Если у кого-то из ребят с решением возникнут проблемы, посоветуйте ему разделить бусины на группы по цветам и искать три одинаковые бусины среди бусин одного цвета.