
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общность начала доказательстваСодержание книги
Поиск на нашем сайте
В дополнение к предыдущему параграфу нужно сказать несколько слов о начале доказательства, как о его сущности, общности; специально проблема начала доказательства будет рассмотрена ниже — в теории доказательства (в последней главе). Содержательную общность доказательства, как системы, представляет начало доказательства, как его принцип, закон или правило, то, чем является сущность доказательства. С точки зрения Аристотеля, начало доказательства, как его сущность, есть закон невозможности противоречия, как закон невозможности утверждения и отрицания одного и того же об одном и том же. Невозможность одновременного утверждения и отрицания представляет природу доказательства. Она имеет характер общности не только в том смысле, что определяет и объясняет все в доказательстве, но и в том смысле, что представляет содержательную общность каждой формы мысли и в виде этой формы является определенным необходимым единством — сущностью. Утверждение и отрицание представляют природу суждения, такую природу имеет и умозаключение. Положение о невозможности противоречия само имеет природу доказательства, поскольку оно носит характер утверждения-отрицания. Сущностью всякого движения, как это достаточно доказано в диалектическом материализме, является единство противоречия. Так должно быть и в логическом доказательстве; его сущностью должно быть логическое осуществление единства противоречия, высказываемое (как это увидим ниже) в умозаключении определенного вида; единство противоречия непосредственно и прямо выражается в логическом, вутверждении чего-либо его же отрицанием, что, как мы уже знаем, имеет природу категории логического и представляет собой логическую рефлексивность. В логике полностью представленное общее есть то, что распространяется и на само себя; но «всем» подразумевается и общность. Это обстоятельство, как это будет показано ниже, не создает никаких трудностей в диалектической логике (тогда как в математической логике создает парадоксы). Логическая схема» и модель
Система аксиом, например система исчисления предложений, и каждая аксиома, как определенная правильно построенная формула, есть логическая схема. Интерпретация этой схемы называется моделью. Модель, в конечном счете, имеет содержательный характер. Логическая система аксиом и теорем в случае моделирования превращается в содержательно истинные предложения модели. Известно, что для установления непротиворечивости, независимости и полноты системы аксиом обращаются к моделированию, к определенной интерпретации (иногда различают друг от друга моделирование и интерпретацию). Мы можем понять знаки предложений х, у, z как арифметические переменные (здесь мы приводим точку зрения Гильберта и Аккермана), значения которых будут 0 и 1; хvу будет арифметическим произведением, Отсюда очевидно, например, то, что — Если переменные х, y, z, принимают значение 0, 1, 2, 3, тогда связь этих переменных v («или») определяется так:
0v0=0v1=0v2=0v3= 0; 1v1=1v2=1v3=1; 2v2=2; 3v3=3; 2v3=2; и т.п.
Здесь мы указываем только на то, что общим для числа, как модели схемы, может быть не схема, а само же число или количество; схема не есть общее, а модель — частное, если «частному» и «общему» придадим соответствующее логическое значение. Модель есть не частное схемы, а ее интерпретация; если «проблема интерпретации есть проблема подстановки чего-то определенного» (Б. Рассел), то ясно, что переменная, как что-то неясное или неопределенное (Черч), не может быть общей в отношении определенного» Слово «модель» понимают по-разному: для некоторых модель вторична, а схема первична, а для других — наоборот; голландский математик Ван-Данцинг сказал, что гор. Париж надо называть моделью его плана, а наоборот, план Парижа есть модель этого города. Мы здесь интересуемся только тем, что между схемой и ее моделью нет отношения общего и частного. Общим Парижа является, ясно, город вообще, а не план Парижа, или наоборот. Нельзя в логике заменять взаимоотношения общего и частного взаимоотношением схемы и модели. В логических формах — в суждении, умозаключении, понятии, доказательстве — действует взаимоотношение общего и частного, а не схемы и модели, которые существенны для математической логики.
ГЛАВА ЧЕТВЕРТАЯ.
Рассмотреть логические законы мысли, наверное, было бы лучше в другом месте, чем здесь, например в конце науки логики, если бы мы следовали принципу развития с начала до конца и полностью реализовали бы его в виде логического развития. Это возможно так и будет при построении полной системы логики, а здесь логические законы могут быть рассмотрены именно в этом месте, поскольку в этом случае, для нас главное характеристика только основных моментов логики; вместе с тем, должна быть подчеркнуто представлена связь логического с онтологическим в начале же науки логики, для того, чтобы ее материалистичность легла в основание ее же диалектичности. Проблема законов логики стоит остро в современных условиях развития логики, когда, например, в математической логике объявляется законом каждое «всегда истинное положение» и нет предела изобилию законов. При рассмотрении логических законов будем руководствоваться принципом диалектики, именно, в том смысле, что начнем с законов старой формальной логики и путем рассмотрения их природы покажем необходимость и существенность законов диалектической логики. Здесь, как мы увидим, выявится, что формальная логика есть момент диалектической логики, формально-логическое представляет одну сторону диалектико-логического; диалектическая логика представляет высшую ступень развития логики, она «высшая логика». Рассмотрению логических законов должно предшествовать определение понятия закона.
О понятии закона
Каков вообще закон науки, таким должен быть и закон, науки логики; но в каждой области действительности, вследствие ее особенностей, действуют особенные законы. Поэтому логические законы специфичны, тем более что они являются законами не действительности, а ее своеобразного отражения — мысли. Логическая связь — необходимая связь, но она как именно связь синтетична. Связь осуществляется тогда, когда подлежащие связи различны. Логическая связь может быть только единством различных. Как известно, единство элементов есть содержание. Единство осуществляется по-разному, разными способами. Это значит, что единство имеет и не может не иметь форму. Способ осуществления единства есть закон. Закон есть форма общности единства. Совершенно по другому представляет природу логического закона математическая логика. В ней логическим законом считается всегда истинное предложение, т.е. такое сложное предложение, которое истинно при всяком значении истинности его составных частей, или логический закон есть изображение, которое составлено из переменных и постоянных и где замена переменных истинными или ложными предложениями всегда дает истинное предложение; это последнее и есть закон. Закон есть всегда истинное положение, например, «закон гипотетического силлогизма»: если А→В и В→С, тогда А→С, или [(А→В)•(В→С)] → (А→С). Этот закон показывает транзитивность импликации. В математической логике закон является выражением функционального отношения; такой закон, по нашему мнению, пригоден и естественен для математики, но он не имеет общелогического характера (как это будет показано в последующем). Закон должен объяснять явления, т.е. он должен быть существенным; закон — категория сущности. Сущность есть у всего существующего, в том числе и у логического. Логический закон представляет собой категорию сущности логического. Если нет закона, тогда имеет место хаос, где все непонятно. Если закон и то, что ему подчиняется, равны друг другу, тогда невозможно существование науки; если закон виден на поверхности явления, тогда наука и научное исследование являются излишними (К. Маркс). Закон не может опережать явление или следовать за явлением (явлениями), в противном случае он был бы не законом, а явлением. Закон является выражением природы явления; определенность этой природы есть форма, которая является для него внутренней. Одним словом, понимание природы закона означает понимание его признаков.
|
||||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.102 (0.011 с.) |

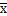 будет
будет 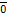 , которое равно 1, и
, которое равно 1, и 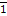 равно 0. На основе такой интерпретации каждое сложное предложение представляет определенную арифметическую функцию основных предложений, которая может иметь только два значения: 0 или 1.
равно 0. На основе такой интерпретации каждое сложное предложение представляет определенную арифметическую функцию основных предложений, которая может иметь только два значения: 0 или 1.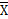 v
v 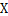 всегда имеет значение 0: поэтому аксиома
всегда имеет значение 0: поэтому аксиома 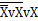 всегда равна 0. То же можно сказать и о других аксиомах.
всегда равна 0. То же можно сказать и о других аксиомах.


