
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие опосредствованного умозаключения в математической логикеСодержание книги
Поиск на нашем сайте
Как было сказано, в математической логике формально-логическое опосредствованное умозаключение, например категорический силлогизм, сводится к условному предложению. «Если А есть В и В есть С, то А есть С». В этом предложении, по мнению Лукасевича, есть единство, тогда как в традиционном понимании категорического силлогизма, отдельное представление посылок и заключения, как трех суждений, не дает этого единства[123]. Из этого видно, что в математической логике единство умозаключения сведено к единству предложения; она не замечает единства умозаключения, если оно выражается различными предложениями; таким образом, здесь отрицается само умозаключение, как определенное опосредствованное единство мысли. Правда, как Гегель, так и Маркс[124] были против разложения умозаключения на посылки и заключение — на отдельные суждения, но признавали необходимое единство умозаключения, как такового, представленного в виде единства трех категорий — «единичного-особенного-общего», что является общей формой умозаключения, тогда как математическая логика общее сводит к схеме, т.е. упраздняет действительную общность. Без общности невозможно понимание не только умозаключения, но и любой формы логического. Для лучшего понимания характера опосредствованного умозаключения в математической логике сравним его с аристотелевской трактовкой силлогизма. В математической логике использован смысл опосредствованного умозаключения, именно, modus ponens, который записывается так: А А → В, В
где А→В есть большая посылка, А — малая, а В — заключение. Эта схема, которая называется схемой умозаключения (или «схемой зачеркивания»), высказывается так: если знаем, что предложение А истинно и А→В правильно, то имеем право сделать вывод об истинности В. В математической логике понятие опосредствованного умозаключения не рассматривается (многие логики не считают modus ponens опосредствованным умозаключением, поскольку в нем нет среднего понятия, а есть только два понятия: А и В), а дается заранее; «схема умозаключения» есть не логическое, а металогическое правило. Доказательство здесь понимается как следствие формул, осуществляемое посредством металогических правил (способом подстановки и схемой умозаключения). Поэтому опосредствование осуществляют именно эти правила (об этом см. в последующем, § 203). В математической логике модус категорического силлогизма Аристотеля Barbara — МаР и SaM, следовательно SaP — принимает вид закона транзитивности импликации: |(М→Р)∙(S→M)| → (S→P). Но в силлогизме могут быть не только общие, но и частные суждения. Превращение частного суждения в общее осуществляют посредством отрицания; например, «некоторые предметы красны» превращается в суждение «не все предметы некрасны». Предикат «некрасный» обозначим через х, но он может обозначать две различные вещи: 1) «не все предметы красны» и 2) «все предметы некрасны». Эту трудность пытаются преодолеть внесением нового символа — помещением соответствующего предиката в вертикальные линии (как это делают Гильберт и Аккерман); «все предметы имеют свойство X» изображается так: |X|; |
SaP соответствует
Этим путем умозаключения Аристотеля превращаются в отношения: исчисления предложений. Но этим теряется главное для опосредствованного умозаключения: внутренняя необходимая опосредствованная осново-следственная связь (Аристотель говорил, что силлогизм касается внутренней мысли, а не внешнего изображения). Нельзя сводить силлогизм к импликации. В исчислении предикатов вывод заключений из посылок (которые не имеют чисто логической природы) производится следующим образом: в посылках есть не только переменные, но и индивидуальные предикаты и индивидуальные предметы. Для обозначения индивидуальных предикатов применяют комбинацию прописных латинских букв с малыми латинскими буквами, например: St, Ms, Dsc. (или греческими, или математическими знаками <, >, =,...). Формальное выведение заключений (формальное доказательство) осуществляется так: символически пишутся посылки и с ними соединяются определенные логические формулы, как основные (аксиомы), вместе с которыми они создают начальные формулы для формальных операций, которые должны осуществляться согласно правилам умозаключения. Для примера возьмем первый модус категорического силлогизма — «все люди смертны, Сократ человек, следовательно, Сократ смертен». Здесь три индивидуальных обозначения. Словам «человек», «смертен» — соответствует два предиката Ms(x) и St(x), для которых общим предметным родом можно считать род живых существ. Третье индивидуальное обозначение — собственное имя «Сократ». Посылками, записанными в виде формул, являются:
(x)(Ms(x)→St(x)) Ms(Сократ).
путем подстановки в формуле: (x)F(x)→F(y) (это аксиома: «если предикат F осуществляется для всех x, тогда он осуществляется также для всех у») получаем:
(x)(Ms(x)→St (x)) → Ms(y)→St(y)
и далее (применением определенного правила):
(х) [Ms(x)→St(x)]→[Ms(Сократ)→St(Сократ)], Ms(Сократ)→St (Сократ), St (Сократ).
Последняя формула есть символическое выражение заключения «Сократ смертен»[125]. Здесь применяется аксиома и одно правило умозаключения, т.е. все подразумевается заранее, и постольку опосредствованное умозаключение пропущено. Превращение формул согласно способу подстановки и правилу умозаключения, осуществляемое здесь, имеет (и в данном случае, и вообще) математически-механический характер, и не является опосредствованным умозаключением в строго логическом смысле. Как известно, из 19 правильных модусов категорического силлогизма в математической логике не оправдывается 4 модуса: модусы III фигуры Darapti и Felapton и модусы IV фигуры Bramalip и Fesaro; т.е. не оправдываются:
1) МаР и MaS, след. SiP 2) МеР и MaS, след. SoP 3) РаМ и MaS, след. SiP 4) РеМ и MeS, след. SoP
Эти модусы неоправданны, якобы, потому, что для их получения нужна дополнительная посылка, что, якобы, Аристотель не учел того, что, например, умозаключение «МаР и MaS, следовательно SiP» правильно тогда, когда дополнительно учитывается, что существуют предметы, входящие в класс М. Гильберт и Аккерман отмечают, что аристотелево понимание общеутвердительного суждения («все А суть В») не полностью соответствует их интерпретации формулы (xvў); положение Аристотеля «все А суть В» считается, истинным, если существуют предметы А. Эти авторы говорят, что их отклонение от Аристотеля оправдывается требованиями математического применения логики[126]. Это означает, что математическое применение логики суживает ее; напр., из 19 правильных модусов остается только 15. Ошибкой является не то, что субъект общеутвердительного суждения подразумевает существование предметов, а то, что исключается их существование. Понятие предмета для логики необходимо. Да и невозможно отрицание понятия предмета; категория предмета есть категория логического, т.е. такое понятие, отрицание которого невозможно и полагает его же. В математической логике все умозаключения являются превращениями, поэтому они непосредственны. В математическом умозаключении нет «среднего понятия», которое внутренне для посылок, как это имеет место в традиционной логике. В математической логике умозаключения не являются опосредствованными, так как умозаключение есть вывод следствия из основания, а здесь вместо осново-следственной связи применяется импликация. Но можно сказать и то, что в математической логике ни одно умозаключение не является непосредственным, поскольку из аксиом ничего не выводится непосредственно, т.е. без применения метаправил. Выведение осуществляется всегда посредством металогических правил; иначе говоря, в математической логике все умозаключения опосредствованны, поскольку они осуществляются посредством метаправил. Но, назначение метаправил заключается в том, что они защищают тавтологичность аксиом (посылок)[127]. Это значит, что метаправила являются правилами выведения, действия и, вместе с тем, правилами не-выведения (в смысле синтетическом) и бездействия. «Правила действия» являются лишними и чуждыми — внешними для умозаключения, его внутренней необходимости. В выведении заключения из посылок не должно действовать ничего, кроме осуществления внутреннего следования. Только внутренняя связь есть необходимая связь; внешняя связь имеет механический характер. В математической логике «умозаключение» осуществляется механически, например посредством подстановок. Поэтому здесь нет умозаключения, как внутренней необходимости; т.е. в математической логике «умозаключение» применяется в другом, специфическом смысле. Главное для логического — внутренняя необходимость; в логических переходах должна действовать внутренняя объективная логика[128]. В математической логике правила умозаключения металогичны, они заранее подразумевают мысль умозаключения: 1) математически — в виде способа подстановки и 2) логически — в виде modus ponens, т.е. мысль умозаключения применяется помимо рассмотрения его природы. Это означает, что математическая логика есть применение логики в определенной сфере. В математической логике такое опосредствованное умозаключение, как категорический силлогизм, рассматривается в исчислении классов, тогда, как: 1) в категорическом силлогизме применяются предикатные суждения, 2) а сведение свойств к классам невозможно. Могут быть тождественными два класса, но не два свойства[129]. Следовательно, правильное понятие опосредствованного умозаключения в математической логике не рассматривается; на его месте ставятся превращения формул, осуществляемые посредством металогических правил.
|
||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

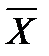 | обозначает «все предметы имеют свойство
| обозначает «все предметы имеют свойство 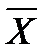 »;
»; 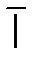 X | обозначает: «неверно, что все предметы имеют свойство X». Постольку:
X | обозначает: «неверно, что все предметы имеют свойство X». Постольку: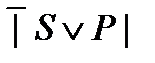 ,
,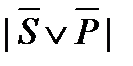 ,
,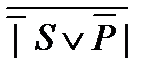 ,
,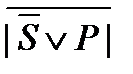 .
.


