Второе начало термодинамики. Цикл Карно

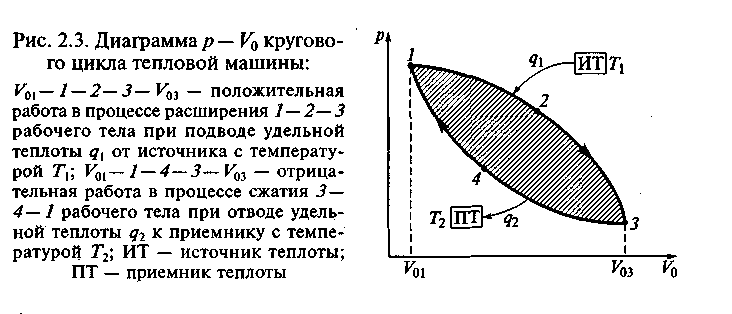
С открытием первого закона термодинамики было осознано значение энергии в материальном мире и доказано, что все виды энергии в конечном счете превращаются в теплоту, которая за­тем рассеивается в окружающей среде. Мера этого рассеивания была названа энтропией. Чем больше рассеивается (обесцени­вается) энергия, тем с большей интенсивностью возрастает эн­тропия в системе. Было установлено, что энергия и энтропия являются неотъемлемыми свойствами материи, причем энер­гию стали признавать мерой движения материи, а энтропию — мерой ее рассеивания (деградации). Однако только с изучения возможности использования теплоты для совершения работы и начинается практическая термодинамика.

Действительно, первый закон термодинамики, констатируя непреложность принципа сохранения количества энергии при ее превращениях, в то же время не дает ответа на главные воп­росы практической теплотехники, а именно: при каких услови­ях, по каким направлениям и какая часть подводимой к рабо­чему телу теплоты может превращаться в работу? Ответы на эти вопросы, составляющие сущность теплотехники, были получе­ны гениальным французским инженером С. Карно еще до от­крытия первого закона термодинамики.

Так, С. Карно установил, что теплота может быть преобразо­вана в механическую работу лишь тогда, когда имеется перепад температур, и величина этой работы зависит только от темпе­ратур, при которых подводится и отводится теплота.

Согласно этому положению, вошедшему в термодинамику как ее второе начало (второй закон), самопроизвольные процес­сы возможны лишь в том случае, когда в системе нет равнове­сия, причем эти процессы всегда протекают в направлении, при котором система приближается к равновесному состоянию.

Второе начало термодинамики первоначально охватывало только процессы преобразования теплоты в работу и имело раз­ные формулировки. Например, часто этот закон выражался таким образом: в круговом процессе располагаемая теплота не может быть полностью преобразована в работу.

Смысл формулировки второго начала термодинамики, пред­ложенной У.Томсоном, сводится к следующему: нельзя пост­роить двигатель, все действие которого сводилось бы только к заимствованию теплоты из одного источника и совершению внеш­ней работы. Такой двигатель называют вечным двигателем вто­рого рода.

Наиболее общая формулировка второго закона термодинами­ки принадлежит Ф. Клаузиусу, согласовавшему положение, выс­казанное С. Карно, с первым законом термодинамики в следу­ющей форме: «Теплота не может самопроизвольно (без компен­сации) переходить от менее нагретого тела к более нагретому». Под компенсацией понимают необходимость совершения неко­его дополнительного процесса, уяснение смысла которого в тех­нической термодинамике осуществляется на весьма абстракт­ных моделях равновесных и обратимых процессов.

Как было отмечено ранее, равновесный процесс, представ­ляемый непрерывным рядом бесконечно близких состояний, можно изобразить линиями на термодинамических диаграммах, например, Понятие обратимости процессов связывают с бесконечно малым изменением параметров состояния термодинамической системы¹.

Наиболее совершенными процессами с точки зрения преоб­разования теплоты в работу являются обратимые круговые процессы — циклы (рис. 2.3) [16]. Так как при их осуществле­нии отсутствуют явления трения и теплообмена рабочего тела с окружающей средой, оно перемещается с бесконечно малыми приращениями скорости и в конце процесса принимает свое начальное состояние. Следовательно, в таких процессах удель­ная теплота воспринимаемая рабочим телом в результа­те ее подвода от источника и отвода к приемнику, не расходует­ся на приращение внутренней энергии рабочего тела и его пе­ремещение, а полностью преобразуется во внешнюю работу / (заштрихованная часть диаграммы). В то же время среди обра­тимых круговых процессов наиболее совершенным будет тот, который имеет наибольший термический КПД:

¹Все реальные термодинамические процессы протекают при конечной разности давлений и температур рабочего тела и окружающей среды. Следо­вательно, реальные процессы всегда неравновесные. Однако техническая тер­модинамика оперирует равновесными процессами, так как в противном слу­чае потребовалось бы существенно усложнить аппарат моделирования посред­ством введения зависимостей параметров состояния от времени.

Наиболее совершенным круговым процессом является обра­тимый круговой процесс, или цикл, Карно, при осуществлении которого может быть достигнут максимальный термический КПД по сравнению с таковым для всех других процессов, про­исходящих при тех же температурах Рассмотрим этот классический процесс более детально.

Анализируя формулу (2.13), отметим, что возрастает при уменьшении и увеличении Это означает, что, выбирая со­ответствующим образом процессы расширения и сжатия, про­текающие с подводом и отводом удельной теплоты мож­но изменять значение термического КПД. В связи с этим воз­никает вопрос: можно ли найти такой цикл, который обладал бы наибольшим КПД?

Такой цикл и был предложен С. Карно. Он состоит из двух обратимых изотермических и двух обратимых адиабатных про­цессов (рис. 2.4). Изотермический и адиабатный процессы наи­более предпочтительны с точки зрения получения максималь­ной работы, поскольку при изотермическом процессе вся теп­лота, подводимая к рабочему телу, превращается в работу, а ади­абатный процесс протекает без теплообмена.

Рассмотрим все процессы цикла Карно. Процесс 1 — 2 — изотермическое расширение рабочего тела при подводе удель­ной теплоты от источника с температурой Количество удельной теплоты равное работе /,, произведенной в про­цессе 1 — 2, определяется по формуле

В процессе адиабатного сжатия 4—1 газ нагревается до тем­пературы Работа, затрачиваемая на сжатие, численно равна площади фигуры и определяется по формуле

Если в процессе 3—4 сжимать газ, не охлаждая его (без от­вода удельной теплоты ), то этот процесс будет адиабатным. Ввиду того что адиабаты являются эквидистантными кривыми (не пересекаются между собой), то через одну точку (точка 3) можно провести лишь одну адиабату. Тогда в результате такого

Рис. 2.4. Диаграммы цикла Карно в координатах р — V₀ (а) и T—s (б):

1—2 — изотермическое расширение; 2—3 — адиабатное расширение; 3—4 — изотермическое сжатие; 4— 1 — адиабатное сжатие; — количество подво­димой удельной теплоты; д₂ — количество отводимой удельной теплоты; ИТ — источник теплоты; ПТ — приемник теплоты

провести лишь одну адиабату. Тогда в результате такого сжатия процесс пойдет не по изотерме 3—4, а по адиабате 3—2. В исходное состояние рабочее тело должно быть возвращено лишь по изотерме, так как при изотермическом процессе на сжа­тие затрачивается наименьшее количество работы. В итоге для сжатия в процессах 3—4 и 4—1 потребуется то же количество работы, которое было получено в процессах расширения 1 — 2 и 2—3. Полезная работа цикла будут равны нулю. Отсюда можно сделать следующий вывод: для того чтобы получить полезную работу, необходимо какую-то часть подведенной теп­лоты безвозмездно отдать в окружающую среду, т. е. потерять.

Полезная работа цикла 1—2—3— 4 определяется алгебра­ической суммой работ, полученных или затраченных в отдель­ных процессах цикла:

(2.14)

Из полученной формулы видно, что работы в адиабатных процессах 2— 3 и 4— 1 взаимно уничтожаются. Тогда формула (2.14) примет вид

 

КПД любого цикла тепловой машины (в том числе цикла Карно) определяется по формуле Отсюда

(2.15)

Для адиабат 2—3 и 4— 1 справедливы следующие соотноше­ния: