Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетика колесного движителяСодержание книги
Поиск на нашем сайте
Структура сопротивления качению автомобиля. Колесный движитель преобразует крутящий момент Мощность
Рис. 4.26. Структура потерь качения колесного движителя Гистерезисные потери, обусловленные упругой деформацией шин и дороги. Гистерезисные потери шин связаны с циклическим воздействием на их элементы, находящиеся в зоне контакта с дорогой: · постоянной нормальной нагрузки Zcoстороны дороги; · тангенциальной нагрузки X, вызываемой передаваемым крутящим моментом · переменной нагрузки · боковой нагрузки Y, возникающей при повороте и крене. Гистерезисные потери дороги обусловлены циклическим воздействием на элементы ее полотна нормальной Шина поглощает большое количество энергии в обратимой форме. Однако не вся энергия возвращается в фазе разгрузки деформированного фрагмента шины: часть ее, расходуемая на молекулярное и механическое трение в материалах, необратимо теряется. Для поддержания качения колеса необходимо пополнять потери энергии, что и осуществляется приложением к оси колеса крутящего момента или толкающей силы. В конструкции шины около 30 % потерь энергии приходится на протектор и 70 % — на каркас.
Рис. 4.27. Упругие характеристики абсолютно жесткого (а), абсолютно эластичного (б) и эластичного (в) тел: Р — нагрузка; h — деформация; В — конечная точка нагружения Абсолютно жесткое либо абсолютно эластичное колесо на абсолютно жесткой либо абсолютно эластичной дороге не испытывает сопротивления качению. При абсолютно жестких колесе и дороге нагрузка Р не вызывает их деформации h (рис. 4.27, а). У абсолютно эластичного тела при прекращении действия деформирующих сил полностью восстанавливается форма (рис. 4.27, б). На практике, однако, реальному эластичному элементу соответствует характеристика с петлей гистерезиса, изображенная на рис. 4.27, в.
Качение эластичного колеса по гладкой жесткой поверхности. Контакт колеса с гладкой жесткой поверхностью считают плоским. Известны четыре вида радиуса колеса (рис. 4.28): три из них определяются геометрически, а один — кинематический — как отношение скорости поступательного движения колеса Колесо преобразует вращательное движение в поступательное с потерями мощности где Силу X определим из схемы, выполненной на рис. 4.28, г, с учетом сноса равнодействующей нормальных реакций дороги Z на величину плеча Тогда
Рис. 4.28. Свободный
где ответственно. В анализе используют коэффициент сопротивления качению шины
где
где При наличии на колесе крутящего момента всегда имеет место частичное скольжение колеса относительно полотна дороги. Это обусловлено разницей продольных напряжений в шине (в набегающей на контакт и уходящей ее частях). Поэтому при малой нормальной нагрузке элементы беговой дорожки еще до выхода из пятна контакта скользят в пятне, причем с увеличением Изменение радиуса качения
где
где Потери при упругом скольжении выражаются формулой
Коэффициент сопротивления качению Физические процессы, обусловливающие снос
Рис. 4.29. Зависимость радиуса качения условный радиус
радиальном направлении. Сжатие радиально ориентированных элементов происходит в набегающей области колеса до момента прохождения элементом вертикальной оси колеса. Затем в сбегающей области происходит их распрямление до нормального состояния. На рис. 4.30 деформируемые элементы представлены в виде элементарных колебательных контуров, имеющих массу Такой элементарный контур в течение каждого цикла работы рассеивает энергию. В каждом вовлекаемом в контакт радиальном срезе колеса непрерывно происходят вынужденные колебания с рассеянием энергии. Движение элемента описывается уравнением
где
Элементарные реакции несимметрична относительно середины контакта: их равнодействующая Z смещена на расстояние Выделяют семь режимов качения колеса: ведущий, свободный, нейтральный, ведомый, тормозной, юз и буксование. В ведущем режиме вся подводимая энергия
В зависимости от типа и состояния опорной поверхности, эластичности шины и режима качения колеса изменяются доли составляющих потерь. При качении ведомого колеса по асфальтобетонной дороге 90...95 % общих потерь — гистерезисные потери, 3...5 % — потери на трение шины об опорную поверхность, 2...3 % — потери на деформацию упругой поверхности, остальное — аэродинамические потери вращающегося колеса. У ведущего и тормозящего колес потери увеличиваются в результате трения в контакте [17]. Качение колеса по деформируемой опорной поверхности. При качении по деформируемой опоре контакт осуществляется по сложной поверхности. Наблюдаются потери на деформацию опоры, обусловливающие дополнительный снос реакцииZ. Представим качение абсолютно жесткого колеса по опоре, для которой характерна лишь упругая деформация (рис. 4.31, а). Подминая поверхность, колесо вынуждено постоянно «выбираться» из лунки, испытывая воздействие продольной составляющей
Рис. 4.31. Схема сил, действующих на колесо при движении по деформируемой опорной поверхности для случая
Деформация обычной шины при движении на мягкой дороге на 30...50 % меньше, чем на твердом покрытии [31]. Колесо, преодолевая силы, возникающие при упругопластической деформации, продавливает колею глубиной
И упругая, и пластическая деформация полотна дороги происходит за счет энергии привода АТС. Общий коэффициент сопротивления качению Взаимодействие колеса с твердым микрорельефом дорожного покрытия. Сопротивление качению зависит от размеров и характера неровностей дороги, которые вызывают дополнительную деформацию шины и затраты энергии. В табл. 4.5 приведены значения коэффициента сопротивления качению шины Коэффициент
Коэффициент сопротивления качению шины для любого покрытия и микрорельефа изменяется пропорционально квадрату скорости'
где .
Рис. 4.32. Характеристики колеса при боковой нагрузке: а, б — формы пятна контакта и эпюры поперечных напряжений Потери в шине при наличии боковой нагрузки. Приложении к колесу боковой силы По мере удаления от входа в контакт напряженность элементов шины возрастает, в задней части площадки поперечные элементарные силы Характер зависимости угла Характеристикой бокового увода является коэффициент сопротивления боковому уводу шины
При боковой нагрузке из-за увода, дополнительной деформации и скольжения шины возрастают потери на ее качение. Дополнительный коэффициент сопротивления качению
где Для шин автомобилей КамАЗ 260 —508Р, например, при нагрузке 2000 дан Влияние эксплуатационных и конструктивных факторов на сопротивление качению колеса. Зависимость радиуса колеса от давления воздуха в шине имеет вид [28]
где Нормальный прогиб шины
где
Нормальная жесткость шины зависит от числа слоев корда в брекере, рисунка протектора, шага и угла наклона грунтозацепов и других факторов. Оценка сопротивления качению колеса Известна формула [28]
где а, Для разогретой шины 260 — 508 модели И-252Б, например, в условиях ее работы в составе задней тележки установке же ее на переднем мосту Увеличение давления воздуха приводит к снижению потерь на качение шины по твердому основанию: повышается ее жесткость и уменьшается радиальная деформация, что вызывает снижение гистерезисных потерь. Зависимости сопротивления качению и энергозатрат от скорости движения монотонно возрастающие: гистерезисные потери с увеличением числа циклов нагружения возрастают в большей мере, чем уменьшаются из-за нагрева шины. Достаточную для практики Точность обеспечивает формула
где
где скорость выражена в км/ч. Тогда для шины 260 — 508 при
Конструктивные параметры шины оказывают большое влияние на коэффициент Увеличение толщины протектора повышает коэффициент, Увеличение отношения ширины обода к ширине профиля шины и уменьшение* отношения высоты профиля шины к его ширине приводят к снижению коэффициента сопротивления качению. Внутреннее строение каркаса шины оказывает влияние на коэффициент сопротивления качению. При Увеличение диаметра колеса приводит к уменьшению коэффициента Увеличение ширины колеса на дорогах с твердым покрытием незначительно повышает коэффициент Совершенствование качества резины позволяет снизить сопротивление качению. Около 60 % потерь на качение связано с гистерезисом резины. Разница в сопротивлении качению высоко- и низкогистерезисных резин может превышать 40 %. Износ рисунка протектора снижает сопротивление качению, особенно у диагональных шин. У шины с полностью изношенным рисунком сопротивление качению при скорости 130 км/ч меньше на 25 % по сравнению с сопротивлением новой шины [31]. Тепловые явления при работе шины. Шина при работе нагревается в результате трения в материалах шины и в плоско-
тангенциальной эластичности и как следствие — уменьшению гистерезисных потерь и сопротивления качению. На рис. 4.33 приведены экспериментально полученные зависимости двух параметров шины 260 — 508 от ее температуры [28]. Снижение сопротивления качению шины с учетом роста давления в ней, сопровождающего прогрев шины, существенно. Например, у шины 1220x400—533 при прогреве ее от 20 до 100 °С сопротивление качению снижается за счет уменьшения гистерезисных потерь на 26%, за счет прироста давления воздуха — на 10 %, а всего — на 36 % [28]. Общие энергозатраты колесного движителя. Суммарные энергозатраты колесного движителя обусловлены сопротивлением качению колес, затратами мощности на колебания АТС и ее дополнительными потерями, возникающими на повороте. Сопротивление качению и затраты мощности на колебания ATС. Работа шин в системе движителя сопровождается дополнительными затратами мощности, вызываемыми неодинаковыми условиями работы шин, неравномерным распределением крутящих моментов по колесам и колебаниями АТС. Под силой сопротивления качению ТС подразумевают потери силы при качении всех колес, приведенные к условной силе, действующей в направлении, противоположном движению ТС [28]:
где Потери на качение шин в составе движителя оценивают единообразно — обобщенным коэффициентом сопротивления качению АТС
где После замены отдельных значений
Кроме сил деформации и скольжения в контактных зонах колес с дорогой имеются силы, вызываемые колебаниями колес, а также циркуляцией мощности. Эти дополнительные силы непрерывно изменяются по величине и направлению, но в среднем их сумма
При средних скоростях движения на изношенном асфальтовом шоссе Например, при движении КамАЗа по асфальтобетонному шоссе с сильно разжиженным битумом Энергия АТС при движении по неровной дороге затрачивается как на преодоление основной горизонтальной составляющей реакции дороги, так и на возбуждение колебаний подрессоренных и неподрессоренных масс. Это потери в амортизаторах Влияние поворота. При боковой нагрузке на АТС углы увода шин могут отличаться. Тогда для расчета силового баланса АТС используют приведенный коэффициент
Общий КПД силовой установки. КПД силовой установки (СУ) ТС, содержащей двигатель, трансмиссию и движитель,
где сомножители в правой части уравнения представляют собой соответствующие Таблица 4.6 КПД преобразователей энергии среднеэксплуатационные значения КПД, реализуемые на множестве эксплуатационных режимов. В табл. 4.6 приведены диапазоны значений КПД СУ и ее элементов легковых и грузовых автомобилей, а также для сравнения — КПД других ТС [14].
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.51.35 (0.016 с.) |

 подводимый к колесам, в продольное усилие
подводимый к колесам, в продольное усилие  приложенное к элементам подвески. Преобразующими элементами являются шины, через них передается воздействие от неровностей дороги на автомобиль. Шины связывают упругую систему трансмиссии с системой подрессоривания АТС. Поэтому потери в шинах зависят от множества взаимосвязанных свойств самих шин, трансмиссии, подвески и дороги, а сопротивление качению является функцией характеристик не только шин и дороги, но и АТС с его системами подрессоривания и трансмиссией.
приложенное к элементам подвески. Преобразующими элементами являются шины, через них передается воздействие от неровностей дороги на автомобиль. Шины связывают упругую систему трансмиссии с системой подрессоривания АТС. Поэтому потери в шинах зависят от множества взаимосвязанных свойств самих шин, трансмиссии, подвески и дороги, а сопротивление качению является функцией характеристик не только шин и дороги, но и АТС с его системами подрессоривания и трансмиссией. затрачиваемая на преодоление сопротивления качению АТС, обусловлена тремя факторами: гистерезисом упругой деформации шин и дороги, внешним трением шин и других элементов движителя, а также пластической деформацией дороги (рис. 4.26).
затрачиваемая на преодоление сопротивления качению АТС, обусловлена тремя факторами: гистерезисом упругой деформации шин и дороги, внешним трением шин и других элементов движителя, а также пластической деформацией дороги (рис. 4.26).
 (тяговым
(тяговым  или тормозным
или тормозным 
 вследствие воздействия микрорельефа дороги;
вследствие воздействия микрорельефа дороги; и касательной
и касательной  сил.со стороны колеса.
сил.со стороны колеса.
 к его угловой скорости
к его угловой скорости 
 которые в случае
которые в случае  и
и  могут быть представлены в виде
могут быть представлены в виде 
 — мощность, подводимая к колесу,
— мощность, подводимая к колесу,  крутящий момент, приложенный к колесу;
крутящий момент, приложенный к колесу; 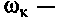 угловая скорость колеса;
угловая скорость колеса;  — мощность, передаваемая от колеса к автомобилю,
— мощность, передаваемая от колеса к автомобилю, 
 бесполезного момента сопротивления (по Кулону):
бесполезного момента сопротивления (по Кулону):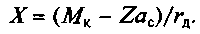


 (а), статический
(а), статический  (б), динамический
(б), динамический  (в) радиусы эластичного колеса и схема равномерного движения (г):
(в) радиусы эластичного колеса и схема равномерного движения (г): —нормальная нагрузка,
—нормальная нагрузка,  — угловая скорость колеса;
— угловая скорость колеса;  — крутящий момент, приложенный к колесу; X — продольная составляющая реакции дорожного полотна; Z— равнодействующая нормальных реакций дороги;
— крутящий момент, приложенный к колесу; X — продольная составляющая реакции дорожного полотна; Z— равнодействующая нормальных реакций дороги;  — снос реакции Z;
— снос реакции Z;  — скорость поступательного движения колеса
— скорость поступательного движения колеса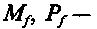 момент и сила сопротивления качению колеса со-
момент и сила сопротивления качению колеса со-

 — составляющая коэффициента
— составляющая коэффициента  характеризующая силовые потери, связанные со сносом ас реакции Z,
характеризующая силовые потери, связанные со сносом ас реакции Z, 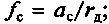
 составляющая коэффициента
составляющая коэффициента  характеризующая кинематические потери, связанные со скольжением колеса
характеризующая кинематические потери, связанные со скольжением колеса 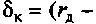
 приводящим к уменьшению скорости движения автомобиля
приводящим к уменьшению скорости движения автомобиля  Коэффициенты
Коэффициенты  называются соответственно энергетическим, силовым {динамическим) и кинематическим коэффициентами сопротивления качению. Величина
называются соответственно энергетическим, силовым {динамическим) и кинематическим коэффициентами сопротивления качению. Величина  определяет дополнительный снос равнодействующей нормальных реакций Z. С учетом того, что
определяет дополнительный снос равнодействующей нормальных реакций Z. С учетом того, что  можно записать
можно записать
 — силовые и кинематические составляющие силы
— силовые и кинематические составляющие силы 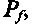 момента
момента 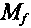 и мощности
и мощности  сопротивления качению колеса.
сопротивления качению колеса. доля скользящих элементов растет. Проскальзывание шин ведущих колес на сухом асфальтобетонном покрытии в крейсерском режиме достигает 2... Ъ%.
доля скользящих элементов растет. Проскальзывание шин ведущих колес на сухом асфальтобетонном покрытии в крейсерском режиме достигает 2... Ъ%. колеса в зависимости от крутящего момента
колеса в зависимости от крутящего момента  при условном отсутствии скольжения
при условном отсутствии скольжения  подчиняется линейной зависимости
подчиняется линейной зависимости
 радиус качения ведомого колеса;
радиус качения ведомого колеса;  — коэффициент тангенциальной эластичности по крутящему моменту (при
— коэффициент тангенциальной эластичности по крутящему моменту (при 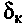 = 0 см. штриховую линию на рис. 4.29). Зависимость
= 0 см. штриховую линию на рис. 4.29). Зависимость  при наличии скольжения элементов шины представлена на рис. 4.29 сплошной линией. Аналогично используют формулу
при наличии скольжения элементов шины представлена на рис. 4.29 сплошной линией. Аналогично используют формулу
 — коэффициент тангенциальной эластичности по окружной силе.
— коэффициент тангенциальной эластичности по окружной силе.
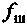 служит измерителем потерь мощности в шине колеса. Он численно равен выраженной в ваттах мощности, теряемой при качении колеса, которое находится под действием нормальной нагрузки
служит измерителем потерь мощности в шине колеса. Он численно равен выраженной в ваттах мощности, теряемой при качении колеса, которое находится под действием нормальной нагрузки 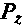 = 1 Н при скорости
= 1 Н при скорости  = 1 м/с. Из уравнений (4.21) и (4.22) следует, что причинами потери мощности являются, во-первых, продольный снос
= 1 м/с. Из уравнений (4.21) и (4.22) следует, что причинами потери мощности являются, во-первых, продольный снос  реакции Z и, во-вторых, неравенство радиусов
реакции Z и, во-вторых, неравенство радиусов  т.е. наличие
т.е. наличие 
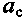 и существенность коэффициента
и существенность коэффициента 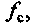 описываются следующим образом. При входе в контакт элементы шины деформируются в
описываются следующим образом. При входе в контакт элементы шины деформируются в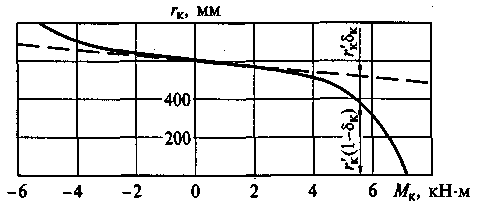
 колеса от крутящего момента
колеса от крутящего момента 
 соответствующий отсутствию скольжения;
соответствующий отсутствию скольжения; наблюдаемый радиус
наблюдаемый радиус  — скольжение колеса
— скольжение колеса
 пружину (связывающую массу с ободом) жесткостью
пружину (связывающую массу с ободом) жесткостью  и демпфер с коэффициентом демпфировании
и демпфер с коэффициентом демпфировании 

 — деформация;
— деформация;  — ускорение и скорость массы
— ускорение и скорость массы 
 —коэффициент сопротивления;
—коэффициент сопротивления;  — элементарная реакция дороги.
— элементарная реакция дороги. в набегающей области больше, чем в сбегающей
в набегающей области больше, чем в сбегающей  Эпюра реакций, показанная на рис. 4.30,
Эпюра реакций, показанная на рис. 4.30, Плечо
Плечо  тем больше, чем больше коэффициент
тем больше, чем больше коэффициент  и скорость
и скорость 
 расходуется на гистерезисные потери шины, работу сил внешнего трения шины о дорогу и вентиляционные потери. В свободном режиме подводимый момент используется только для качения колеса. Для нейтрального режима характерны
расходуется на гистерезисные потери шины, работу сил внешнего трения шины о дорогу и вентиляционные потери. В свободном режиме подводимый момент используется только для качения колеса. Для нейтрального режима характерны  В ведомом режиме
В ведомом режиме 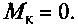 В тормозном режиме к колесу подводится тормозной момент
В тормозном режиме к колесу подводится тормозной момент 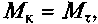 направленный в сторону, противоположную
направленный в сторону, противоположную  а накопленная кинетическая энергия АТС расходуется на трение шины о дорогу и гистерезисные потери в полотне дороги.
а накопленная кинетическая энергия АТС расходуется на трение шины о дорогу и гистерезисные потери в полотне дороги. равнодействующей Z элементарных нормальных реакций N. Эпюра элементарных нормальных сил в опорном слое соответствует его деформации: рост от краев лунки А: и я к краевым точкам
равнодействующей Z элементарных нормальных реакций N. Эпюра элементарных нормальных сил в опорном слое соответствует его деформации: рост от краев лунки А: и я к краевым точкам 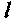 и т пятна контакта с колесом и значительное увеличение нагрузки под пятном, причем со смещением равно-
и т пятна контакта с колесом и значительное увеличение нагрузки под пятном, причем со смещением равно-
 =const:
=const: качение абсолютно жесткого колеса по упругодеформируемой опоре; б — качение шины по мягкой опоре, подверженной упругопластической деформации; /, т — краевые точки пятна контакта; к, п — краевые точки лунки;
качение абсолютно жесткого колеса по упругодеформируемой опоре; б — качение шины по мягкой опоре, подверженной упругопластической деформации; /, т — краевые точки пятна контакта; к, п — краевые точки лунки; 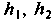 — глубина колеи в набегающей и выходящей части колеса;
— глубина колеи в набегающей и выходящей части колеса;  — снос реакцииZ;
— снос реакцииZ;  — дополнительный снос реакцииZ;
— дополнительный снос реакцииZ;  — крутящий момент, приложенный к колесу действующейZна плечо
— крутящий момент, приложенный к колесу действующейZна плечо  и формированием коэффициента упругого сопротивления грунта
и формированием коэффициента упругого сопротивления грунта 

 (рис. 4.32, б), но после его прохождения упругие силы частично распрямляют полотно, уменьшая глубину колеи до величины
(рис. 4.32, б), но после его прохождения упругие силы частично распрямляют полотно, уменьшая глубину колеи до величины  Общее сопротивление грунта качению
Общее сопротивление грунта качению  может быть представлено суммой
может быть представлено суммой  — коэффициент сопротивления сил пластической деформации грунта качению колеса.
— коэффициент сопротивления сил пластической деформации грунта качению колеса. можно представить в виде суммы
можно представить в виде суммы 
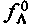 при скорости, близкой к нулю, для дорожных покрытий различных типов.
при скорости, близкой к нулю, для дорожных покрытий различных типов. для любого покрытия можно выразить через значение для гладкого покрытия
для любого покрытия можно выразить через значение для гладкого покрытия  и добавку
и добавку 

 [28]:
[28]:
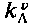 — коэффициент, зависящий от характеристик микрорельефа.
— коэффициент, зависящий от характеристик микрорельефа.
 соответственно для неподвижного и движущегося колес; в — зависимость угла бокового увода
соответственно для неподвижного и движущегося колес; в — зависимость угла бокового увода  от боковой реакции
от боковой реакции  коэффициент сцепления
коэффициент сцепления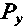 шина и пятно контакта теряют симметрию, и возникает боковая реакция
шина и пятно контакта теряют симметрию, и возникает боковая реакция  (рис. 4.32, а Деформация новых участков шины приводит к перемещению плоскости колеса в направлении действия силы
(рис. 4.32, а Деформация новых участков шины приводит к перемещению плоскости колеса в направлении действия силы  Колесо катится уже в направлении вектора его скорости
Колесо катится уже в направлении вектора его скорости  под углом бокового увода
под углом бокового увода  к плоскости вращения (рис. 4.32, б).
к плоскости вращения (рис. 4.32, б). возрастают, и начинается проскальзывании элементов шины. При этом эпюра сил
возрастают, и начинается проскальзывании элементов шины. При этом эпюра сил  принимает форму, при веденную на рис. 4.32, б.
принимает форму, при веденную на рис. 4.32, б. от боковой реакции
от боковой реакции  иллюстрирует рис. 4.32, в. При малых
иллюстрирует рис. 4.32, в. При малых  угол
угол 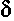 изменяется пропорционально
изменяется пропорционально  Однако с ростом
Однако с ростом  прогрессирует процесс скольжения, и зависимость становится нелинейной уже при угла; увода 2...4°.
прогрессирует процесс скольжения, и зависимость становится нелинейной уже при угла; увода 2...4°. Величина
Величина  зависит от множества факторов. С ростом нормальной нагрузки
зависит от множества факторов. С ростом нормальной нагрузки шина становится жестче и
шина становится жестче и  повышается. При увеличении тяговой силы сопротивляемость шин боковому уводу уменьшается. При возрастании тормозной силы она сначала повышается, а затем падает.
повышается. При увеличении тяговой силы сопротивляемость шин боковому уводу уменьшается. При возрастании тормозной силы она сначала повышается, а затем падает.
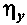 — удельная боковая сила,
— удельная боковая сила, 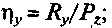 принято, что
принято, что 
 Нетрудно подсчитать, что для этого автомобиля при нагрузке на переднее колесо
Нетрудно подсчитать, что для этого автомобиля при нагрузке на переднее колесо  = 2000 дан и угле его увода
= 2000 дан и угле его увода  (0,1 рад) коэффициент сопротивления качению колеса увеличивается на величину
(0,1 рад) коэффициент сопротивления качению колеса увеличивается на величину  Это значение получено при
Это значение получено при 
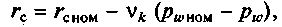
 — свободный радиус при номинальном давлении воздуха;
— свободный радиус при номинальном давлении воздуха;  — константа для шин одной модели;
— константа для шин одной модели; 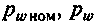 — соответственно номинальное и текущее давления воздуха в шине. Для шин 260 —508 модели И-252Б
— соответственно номинальное и текущее давления воздуха в шине. Для шин 260 —508 модели И-252Б 
 = 519 мм,
= 519 мм,  = 1,45
= 1,45 
 в функции внутреннего давления
в функции внутреннего давления  и нормальной нагрузки
и нормальной нагрузки  определяется по формуле
определяется по формуле
 — постоянный для данной шины коэффициент,
— постоянный для данной шины коэффициент, 
 —нормальная нагрузка, даН;
—нормальная нагрузка, даН;  — атмосферное давление
— атмосферное давление  — давление воздуха в шине,
— давление воздуха в шине, 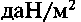 [28].
[28]. в ведомом режиме при
в ведомом режиме при 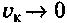 на сухой плоской твердой поверхности в зависимости от давления
на сухой плоской твердой поверхности в зависимости от давления  и нагрузки
и нагрузки  носит базовый характер для представления всех других режимов колеса и условий движения.
носит базовый характер для представления всех других режимов колеса и условий движения.
 — постоянные для шин одной модели; величина
— постоянные для шин одной модели; величина 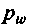 выражена в даН/см2.
выражена в даН/см2. При
При

 — коэффициент при
— коэффициент при  — скорость, м/с [17]. Применяется также модификация последней формулы:
— скорость, м/с [17]. Применяется также модификация последней формулы: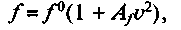

 на скорости 80 км/ч в ведомом режиме
на скорости 80 км/ч в ведомом режиме 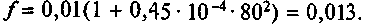
 и, следовательно, на количество поглощаемой ею энергии.
и, следовательно, на количество поглощаемой ею энергии. особенно у диагональных шин. При износе шин сопротивление качению падает (у полностью изношенных — на 20...25 %) [17].
особенно у диагональных шин. При износе шин сопротивление качению падает (у полностью изношенных — на 20...25 %) [17]. коэффициент
коэффициент  радиальных шин меньше, чем у диагональных, на 15... 20 %.
радиальных шин меньше, чем у диагональных, на 15... 20 %. Чем больше размеры и число неровностей на дороге и чем выше на таких дорогах скорость движения,, тем значительнее влияние Диаметра колеса на коэффициент
Чем больше размеры и число неровностей на дороге и чем выше на таких дорогах скорость движения,, тем значительнее влияние Диаметра колеса на коэффициент  [31].
[31]. но на деформируемых опорных поверхностях существенно снижает его. На АТС со сдвоенными колесами из-за неравномерного распределения нормальных нагрузок и крутящих моментов между шинами возникают дополнительные потери на качение.
но на деформируемых опорных поверхностях существенно снижает его. На АТС со сдвоенными колесами из-за неравномерного распределения нормальных нагрузок и крутящих моментов между шинами возникают дополнительные потери на качение.

 — сила сопротивления качению
— сила сопротивления качению  колеса;
колеса;  — нормальная нагрузка на
— нормальная нагрузка на  колесо;
колесо;  — коэффициент сопротивления качению
— коэффициент сопротивления качению  колеса.
колеса.
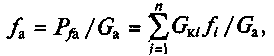
 — вес автомобиля.
— вес автомобиля. осредненным
осредненным  имеем
имеем
 всегда приводит к увеличению мощности потерь
всегда приводит к увеличению мощности потерь  на величину
на величину  что может быть учтено соответствующим увеличением коэффициента
что может быть учтено соответствующим увеличением коэффициента 

 составляют 5...10 %, на ровном булыжнике — 30...50 %, на хорошей грунтовой дороге — 10...30 % значений
составляют 5...10 %, на ровном булыжнике — 30...50 %, на хорошей грунтовой дороге — 10...30 % значений 
 = 0,019, а по сухой грунтовой накатанной степной дороге
= 0,019, а по сухой грунтовой накатанной степной дороге  = 0,032 [28].
= 0,032 [28]. рессорах
рессорах  и шинах
и шинах  [28].
[28]. например,
например, где L — база, а и b — расстояния от центра масс автомобиля до осей [17]. Дополнительная составляющая коэффициента сопротивления качению АТС
где L — база, а и b — расстояния от центра масс автомобиля до осей [17]. Дополнительная составляющая коэффициента сопротивления качению АТС  определяется по формуле (4.23) с учетом
определяется по формуле (4.23) с учетом  На рис. 4.34 приведена зависимость коэффициента сопротивления качению
На рис. 4.34 приведена зависимость коэффициента сопротивления качению  грузового автомобиля от скорости и радиуса кривизны траектории движения [28].
грузового автомобиля от скорости и радиуса кривизны траектории движения [28].