
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания диссипативной системы с одной степенью свободыСодержание книги
Поиск на нашем сайте
Рассмотрим линейную диссипативную систему, движение которой описывается дифференциальным уравнением относительно обобщенной координаты
где значения; Уравнение (4.4) может быть представлено в другом виде:
где частота соответствующей консервативной системы:
Собственная частота демпфированной системы
Общее решение уравнения (4.5) имеет вид
где F и G — действительные постоянные величины. При при
тухание будет монотонным. Значение ческим. Кроме
При ношение энергии, рассеянной за цикл колебаний, к полной энергии процесса. Логарифмический декремент колебаний
Параметр
Диссипативные характеристики механических систем Диссипативные силы. При колебаниях происходит необратимое рассеяние энергии, вызываемое диссипативными силами
Рис. 4.6. Характеристики диссипативных сил при вязком трении (а), больших виброскоростях (б) и сухом трении (в): Вязкое трение, свойственное диссипативным силам, возникающим при малых колебаниях в вязкой среде (рис. 4.6, а), описывается уравнением (4.6)
где При больших виброскоростях имеет место квадратичная зависимость диссипативной силы от скорости (рис. 4.6, б):
где Часто в конструкциях демпферов используют элементы сухого трения (рис. 4.6, в) с характеристикой
(4.8) где Приведенные зависимости представимы единым уравнением
где и 0, имеем уравнения (4.6) —(4.8)). Гистерезис. При циклическом деформировании упругодис-сипативного элемента (рис. 4.7) обнаруживается гистерезис — несовпадение линий нагрузки и разгрузки на диаграмме сила — перемещение (рис. 4.8).
Допустим, что характеристика элемента с линейной упругой составляющей
Площадь петли гистерезиса характеризует энергию
Рис. 4.8. Петли гистерезиса при циклическом деформировании упруго-диссипативного элемента в условиях вязкого трения (а), больших виброскоростей (б) и сухого трения (в):
Петля гистерезиса такого элемента с линейно изменяющейся диссипативной силой в соответствии с уравнением (4.6) при деформировании по закону
Рассеянная энергия элемента, отвечающего зависимости (4.7), для которого петля гистерезиса приведена на рис. 4.8, б,
При наличии зависимости (4.8) рассеянная энергия элемента (рис. 4.8, в)
Рассеянная энергия элемента, характеризуемого зависимостью (4.9),
где На значения
Потери энергии на сухом трении больше внутренних потерь на порядок величины. Коэффициент поглощения
Согласно уравнениям (4.11) —(4.14) коэффициент у является функцией: частоты — при вязком трении (уравнение (4.6)):
амплитуды — при сухом трении (уравнение (4.8)):
амплитуды и частоты — в общем случае (уравнение (4.9)):
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 909; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.149 (0.006 с.) |


 (4.4)
(4.4) — коэффициент диссипации, принимающий любые
— коэффициент диссипации, принимающий любые
 (4.5)
(4.5) — коэффициент демпфирования,
— коэффициент демпфирования,  — собственная
— собственная


 колебания системы носят периодический характер,
колебания системы носят периодический характер, затухают во времени, принарастают.
затухают во времени, принарастают.  Если
Если 
 то затухание сопровождается колебаниями. При
то затухание сопровождается колебаниями. При 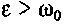 за-
за-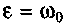 называют крити-
называют крити- используют безразмерные характеристики демпфирования
используют безразмерные характеристики демпфирования
 коэффициент поглощения
коэффициент поглощения  представляет от-
представляет от- равен натуральному логарифму отношения двух последовательных максимальных значений обобщенной координаты:
равен натуральному логарифму отношения двух последовательных максимальных значений обобщенной координаты:
 называют относительным демпфированием. Критическому демпфированию соответствуют значения
называют относительным демпфированием. Критическому демпфированию соответствуют значения 
 Параметр
Параметр 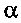 называют коэффициентом затухания.
называют коэффициентом затухания.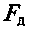 неупругого сопротивления. Их представляют в виде функций скорости движения масс или скорости деформации элементов системы (основные формы зависимости
неупругого сопротивления. Их представляют в виде функций скорости движения масс или скорости деформации элементов системы (основные формы зависимости  приведены на рис. 4.6).
приведены на рис. 4.6).
 — параметры уравнений (4.6) — (4.8)
— параметры уравнений (4.6) — (4.8)
 — постоянная величина.
— постоянная величина. (4.7)
(4.7) — постоянная величина.
— постоянная величина.
 — сила сухого трения
— сила сухого трения 
 (4.9)
(4.9) — постоянные величины (при значениях
— постоянные величины (при значениях  равных 1, 2
равных 1, 2


 имеет вид
имеет вид
 рассеянную в течение цикла деформирования и равно работе диссипативных сил:
рассеянную в течение цикла деформирования и равно работе диссипативных сил:
 —диссипативная сила
—диссипативная сила (4.10)
(4.10) имеет вид эллипса (рис. 4.8, а). Угол
имеет вид эллипса (рис. 4.8, а). Угол  наклона его большой оси характеризует жесткость элемента
наклона его большой оси характеризует жесткость элемента  Энергия, рассеянная за цикл, согласно уравнению (4.10)
Энергия, рассеянная за цикл, согласно уравнению (4.10) (4.11)
(4.11)
 (4.13)
(4.13) (4,14)
(4,14)
 влияет величина
влияет величина 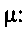

 Величина
Величина  (см. подразд. 4.3.2) равна отношению энергии, потерянной за цикл, к наибольшему значению потенциальной энергии П упругого элемента. При наличии у элемента линейной упругой характеристики
(см. подразд. 4.3.2) равна отношению энергии, потерянной за цикл, к наибольшему значению потенциальной энергии П упругого элемента. При наличии у элемента линейной упругой характеристики  и коэффициент поглощения
и коэффициент поглощения
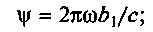 (4.15)
(4.15) (4.16)
(4.16) (4.17)
(4.17)


