
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тогда для конечного процессаСодержание книги
Поиск на нашем сайте
Таким образом, физический смысл энтальпии состоит в том, что в изобарных процессах ее изменение равно теплоте, поглощенной или отданной системой. Энтальпия идеального газа, так же, как и внутренняя энергия, является функцией только температуры и не зависит от объема и давления (поскольку не принимаются во внимание силы взаимодействия между молекулами):
При подводе или отводе теплоты температура любого тела соответственно повышается или понижается. Исследования показали, что для одинакового повышения температуры различных тел требуется разное количество теплоты, т. е. способность тел поглощать теплоту зависит от их свойств и природы. Так появились понятия теплоемкости газов и газовых смесей. Количество теплоты, которое необходимо сообщить телу, имеющему единичную массу, для нагревания его на 1 °С, называется его удельной теплоемкостью с. Теплоемкость твердых и жидких тел зависит от температуры, при которой они подвергаются нагреванию. Однако для небольших диапазонов температур изменения теплоемкости незначительны, поэтому ее можно считать постоянной. Что касается теплоемкости газов, то она изменяется не только с температурой и давлением, при которых происходит их нагревание, но и в зависимости от внешних условий в процессе нагревания. Количество теплоты, которое необходимо подвести для нагревания единицы массы газа на 1 °С при постоянном давлении, называется удельной теплоемкостью ср при постоянном давлении. Количество же теплоты, требующееся для нагревания единицы массы газа на 1 °С при постоянном объеме, называется удельной теплоемкостью cv при постоянном объеме. Кроме того, следует отличать среднюю теплоемкость тела от истинной. Если для нагревания единицы массы тела от температуры При нагревании любого тела при постоянном объеме вся теплота, подводимая к нему, затрачивается только на повышение температуры, или увеличение его внутренней энергии. При нагревании тела при постоянном давлении теплота расходуется не только на повышение температуры, но и на преодоление внешнего давления, так как тело при нагревании расширяется. Следовательно, в последнем случае к нему необходимо подводить большее количество теплоты, чем в первом. Это означает, что теплоемкость ср при постоянном давлении больше теплоемкости
Если единицу массы газа нагревать от абсолютного нуля до температуры Т при постоянном объеме, то количество теплоты, которое нужно подвести к нему, или количество теплоты, воспринятое газом, будет соответствовать его внутренней энергии:
Если же единицу массы газа нагревать от абсолютного нуля до температуры Т при постоянном давлении, то количество теплоты, которое следует подвести к нему, будет соответствовать его удельной энтальпии:
Подставляя в уравнение (2.6) вместо du величину cvdT согласно (2.9), а вместо dl величину pdV0 из (2.7), получим
Преобразовав уравнение (2.10), получим
Правая часть уравнения (2.11) представляет собой полный дифференциал некоторой функции, независимыми переменными которой являются
где s — удельное выражение величиныS, которую Р. Клаузиус назвал энтропией, что означает «превращение». В современной теплотехнике эта величина играет чрезвычайно важную роль, особенно в вопросах, связанных с исследованиями тепловых процессов. Таким образом, можно записать
Следовательно, энтропия представляет собой такую величину, бесконечно малое приращение которой равно отношению бесконечно малого приращения теплоты к абсолютной температуре, при которой эта теплота подводилась к телу. Из равенств (2.12) следует, что энтропия есть не что иное, как один из сомножителей в выражении для определения тепловой энергии. В теплотехнике условно принимают, что для любого тела при атмосферном давлении и температуре -273 °С, или О К, энтропия равна нулю (S0 = 0). Для других же состояний энтропия рассматривается как положительное или отрицательное приращение относительно ее нулевого значения. Следовательно, энтропию можно рассматривать как функцию состояния термодинамической системы.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.113 (0.008 с.) |

 .
.
 требуется подвести количество теплоты q, то величина
требуется подвести количество теплоты q, то величина  называется средней удельной теплоемкостью тела в диапазоне температур от
называется средней удельной теплоемкостью тела в диапазоне температур от  . При уменьшении разности температур
. При уменьшении разности температур  средняя удельная теплоемкость тела приближается к истинной. Если для повышения температуры единицы массы тела на бесконечно малую величину dt необходимо подвести к нему количество теплоты, равное
средняя удельная теплоемкость тела приближается к истинной. Если для повышения температуры единицы массы тела на бесконечно малую величину dt необходимо подвести к нему количество теплоты, равное  то величина
то величина  называется истинной удельной теплоемкостью тела.
называется истинной удельной теплоемкостью тела. при постоянном объеме.
при постоянном объеме. (2.9)
(2.9)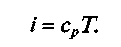
 (2.10)
(2.10) (2.11)
(2.11) Обозначив эту функцию s, а ее бесконечно малое приращение ds и подставив последнюю величину в уравнение (2.11), получим
Обозначив эту функцию s, а ее бесконечно малое приращение ds и подставив последнюю величину в уравнение (2.11), получим
 (2.12)
(2.12)


