
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
После деления первого из них на второе получимСодержание книги
Поиск на нашем сайте
Прологарифмируем последнее соотношение: Формула (2.16) с учетом (2.15), примет вид
Анализируя выражение (2.17), приходим к выводу о том, что значение Формула (2.17) также показывает, что при Анализ цикла Карно позволяет сделать также следующий важный вывод: невозможно превращение теплоты в работу без компенсации. Особенности формулировок второго закона термодинамики, содержащих понятие компенсации, связаны со спецификой этого понятия. Необходимо учитывать, что различают компенсацию двух родов. Компенсация первого рода имеет место в случае, когда процесс превращения теплоты в работу сопровождается изменением термодинамического состояния рабочего тела. Например, при изотермическом расширении идеального газа его внутренняя энергия остается постоянной, и вся теплота, сообщаемая газу, превращается в работу. Увеличение объема газа, представляющее собой компенсацию первого рода, является здесь необходимым условием превращения теплоты в работу. Если превращение теплоты в работу влечет за собой изменение состояния не только рабочего тела, но и других тел, то речь идет о компенсации второго рода. В тепловых машинах такими телами обычно являются приемники теплоты. Что такое компенсация второго рода, наиболее просто понять из следующей формулировки второго закона термодинамики (формулировка М. Планка): «Невозможно построить периодически действующую тепловую машину, которая не производила бы ничего другого, кроме поднятия груза и охлаждения источника теплоты». Из этой формулировки следует, что для превращения теплоты в работу недостаточно только процесса передачи теплоты от источника к рабочему телу. По второму закону термодинамики здесь предполагается наличие некоторого дополнительного процесса. Для теплового двигателя таким процессом является передача теплоты к ее приемнику. Этот дополнительный процесс и представляет собой компенсацию второго рода. В природе существуют процессы, протекающие самостоятельно, без сопровождения другими процессами (без компенсации). Они называются самопроизвольными, естественными или некомпенсированными. Примером самопроизвольного процесса служит превращение работы в теплоту при трении, не сопровождающееся какими-либо другими процессами. Работа здесь полностью превращается в теплоту, тогда как обратный процесс превращения теплоты в работу нельзя провести без компенсации. Процессы, которые не могут протекать без какого-либо сопутствующего дополнительного процесса, называются несамопроизвольными. В природе существует ряд процессов, протекающих самопроизвольно лишь в одном направлении. Например, переход теплоты от горячего тела к холодному — самопроизвольный процесс, но обратный переход теплоты от холодного тела к горячему без каких-либо дополнительных процессов невозможен. В реальных циклах тепловых двигателей (например, в двигателях внутреннего сгорания) цикл Карно неприменим, поскольку из-за небольшого различия в наклонах изотерм и адиабат пришлось бы использовать цилиндры очень большой длины. В современной термодинамике второе начало имеет еще и статистическое толкование. Как известно, в основе молекулярно-кинетической теории лежат статистические представления, относящиеся к большому числу частиц. Хаотичность молекулярного движения приводит к тому, что в макромасштабе проявляются новые, статистические закономерности, которые отличаются от динамических закономерностей механики, присущих отдельным молекулам [16]. Следовательно, молекулярно-кинетическая теория не является механической теорией, хотя каждая молекула строго подчиняется законам механики. В макромасштабе происходит усреднение всех характеристик молекулы: энергии, скорости и др. Понятие температуры относится к множеству молекул макроскопического тела и неприменимо к отдельной молекуле; давление газа является статистически усредненной силой действия большого числа молекул на единицу площади. Каждое термодинамическое состояние газа не является безусловно обязательным, а существует с той или иной вероятностью. Последняя тем выше, чем большим числом комбинаций в пространственном расположении молекул и скоростях молекул оно способно осуществиться. Наименее вероятно состояние газа, при котором скорости молекул совершенно одинаковы, поскольку оно реализуется лишь одним способом. Вероятность такого состояния условно можно определить величиной w0. Тогда вероятность состояния w с разными скоростями во много раз выше, чем w0, так как для разных скоростей можно осуществить большее число комбинаций. Отношение W= w/w0 носит название термодинамической вероятности или статистического веса состояния, причем очевидно, что W>> 1. В статистической физике доказывается в общем случае (а не только для газа), что энтропия тем выше, чем большим числом комбинаций может реализоваться данное состояние. Следовательно, существует взаимосвязь между энтропией S и термодинамической вероятностью W состояния. Соотношение, устанавливающее эту взаимосвязь, было получено Л. Больцманом. На основании статистических соображений он показал, что энтропия прямо пропорциональна логарифму термодинамической вероятности:
где k — отношение универсальной газовой постоянной к постоянной Авагадро, т. е. Таким образом, максимуму энтропии отвечает наиболее вероятное состояние системы. Ввиду того что энтропия связана функциональной зависимостью с вероятностью состояния, второй закон термодинамики, строго говоря, нельзя считать точным. Его более корректная формулировка такова: весьма вероятно, что энтропия изолированной системы возрастает. Следовательно, возможны отступления от этого закона. Для макросистем, содержащих большое число молекул, они крайне маловероятны, но могут оказаться существенными для небольшого числа молекул. Такие отступления, обнаруженные при изучении броуновского движения, были названы флуктуациями. Глава 3
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.54.210 (0.006 с.) |

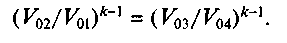
 (2.16)
(2.16)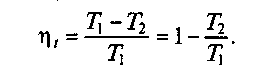 (2.17)
(2.17) может быть равно единице лишь при
может быть равно единице лишь при  либо
либо  но эти условия невозможно осуществить даже в идеальном цикле.
но эти условия невозможно осуществить даже в идеальном цикле. термический
термический  Это означает, что превращение теплоты в работу в случае равенства температур источника и приемника теплоты невозможно. Отсюда следует еще одно (сформулированное В. Оствальдом) определение вечного двигателя второго рода как теплового двигателя, с помощью которого можно было бы получать полезную работу при отсутствии разности температур источника и приемника теплоты. Согласно второму началу термодинамики такой тепловой двигатель невозможен.
Это означает, что превращение теплоты в работу в случае равенства температур источника и приемника теплоты невозможно. Отсюда следует еще одно (сформулированное В. Оствальдом) определение вечного двигателя второго рода как теплового двигателя, с помощью которого можно было бы получать полезную работу при отсутствии разности температур источника и приемника теплоты. Согласно второму началу термодинамики такой тепловой двигатель невозможен.
 Цж/К. Величина к называется постоянной Больцмана.
Цж/К. Величина к называется постоянной Больцмана.


