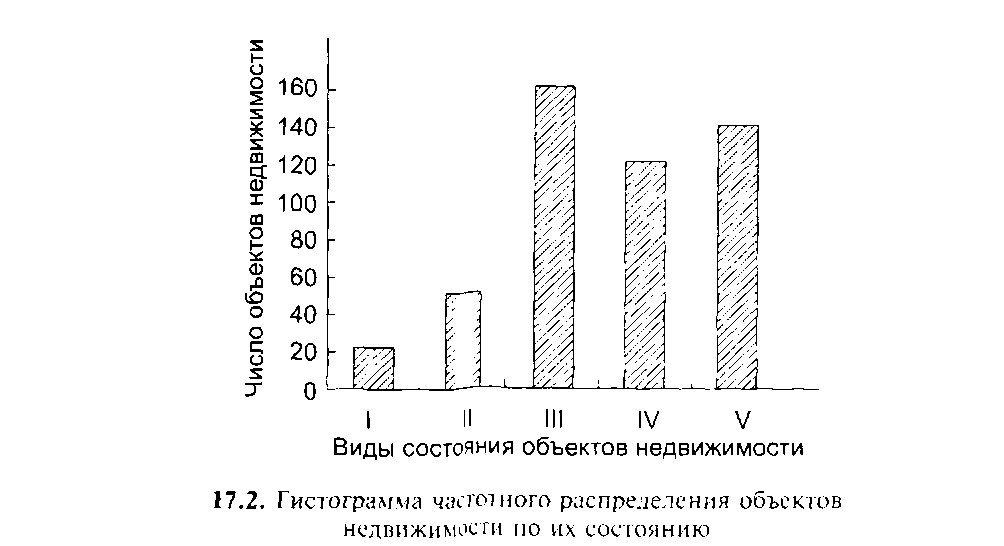
Частотное распределение объектов недвижимости по их сосоянию

 

 

Рассмотренные статистические характеристики отражают распределе­ние объектов недвижимости в статистической выборке по одной перемен­ной (цена продаж, площадь, состояние или местоположение и др.). Ос­новная цель массовой оценки недвижимости — моделирование ее стоимо­сти в зависимости от множества факторов. В этом случае стоимость недвижимости является зависимой переменной от соответствующих не­зависимых переменных. Если предположить, что имеются рыночные данные по сделкам с недвижимостью, то появляется возможность элиминирования (выявления) влияния каждого рассматриваемого фактора на стоимость не­движимости с помощью построения адекватной модели стоимости.

 

 

Построение «оценочной» модели на базе анализа рыночных данных зависит от применяемого методического подхода к оценке стоимости недвижимости. При затратном подходе факторы предложения на рынке недвижимости базируются на принципе замещения, а следовательно, ка­либровка модели проводится исходя из анализа состояния рынка строи­тельно-монтажных работ и материалов с учетом сложившейся нормы при­были для инвесторов (застройщиков). Калибровка модели факторов спроса

 

 

(местоположение, сложившийся порядок исчисления износа и различ­ные рыночные поправки) отслеживаются по изменению конъюнктуры рынка недвижимости.

При сравнительном подходе калибровка модели проводится на осно­ве анализа рыночных данных соответствующего регионального рынка недвижимости в соответствии с принципами оценки: спроса и предло­жения, вклада и замещения.

При доходном подходе для применения метода прямой капитализа­ции в моделировании стоимости доходной недвижимости основная за­дача при калибровке модели состоит в выявлении ставок капитализации на базе анализа данных по рынку недвижимости. Дисконтирование де­нежных потоков требует также дополнительной информации и по дру­гим рынкам (например, финансовому).

Независимо от применяемого подхода при моделировании массовой оценки недвижимости требуется применение многофакторных стати­стических методов: многомерного регрессионного анализа; специаль­ной алгоритмической процедуры обратной связи, позволяющей одновре­менно проанализировать влияние всех рассматриваемых факторов (неза­висимых переменных) на стоимость недвижимости.

Все параметры, характеризующие объекты недвижимости, можно под­разделить на две основные группы: количественные и качественные.

Параметры первой группы непосредственно вводят в модель в каче­стве независимых переменных (общая или полезная площадь, возраст здания, количество спален и т.д.). В определенных случаях не исключа­ется «промежуточное» преобразование количественных параметров в ка­чественные с последующим восстановлением их количественного изме­рения и ввода в модель. Например, рыночные данные о возрасте зданий сначала могут быть классифицированы по группам (1 — 1—10 лет; II — 11 — 30 лет; III — 31-50 лет; IV — свыше 50 лет), а далее эти возрастные группы зданий будут введены в модель с помощью относительных (нор­мированных) числовых значений.

Параметры второй группы отражают качественные характеристики объектов недвижимости, их полезность и привлекательность (табл. 17.4) и требуют определенных преобразований для ввода их в модель в каче­стве независимых переменных. Независимые переменные могут быть пре­образованы путем идентификации качественных параметров с помощью бинарных и скалярных (действительных) чисел.

 

Таблица 17.4

Качественные параметры офисного здания

 

 

Транспортная доступность к зданию	Наличие автостоянки	Физическое состояние здания
Плохая Средняя Хорошая Очень хорошая	Имеется на 20 автомобилей Имеется на 40 автомобилей Отсутствует	Плохое Удовлетворительное Хорошее Отличное

 

 

Пример. Качественный параметр офисного здания (см. табл. 17.4) «наличие автостоянки у офисного здания» можно закодировать двумя бинарными числами (переменными): «имеется автостоянка на 20 авто­мобилей» (0 или 1); «имеется автостоянка на 40 автомобилей» (0 или 1)-и «автостоянка отсутствует» (0 или 1). Таким образом, появляется воз­можность измерить в модели вклад в стоимость офисного здания нали­чия автостоянки на 20 или 40 автомобилей и потери его стоимости при отсутствии таковой. Стоимостное измерение этого вклада (или потери) происходит в процессе калибровки модели с помощью «настройки» со­ответствующих коэффициентов при этих бинарных переменных.

Качественные параметры преобразуются с помощью скалярных чи­сел по алгоритму, отражающему относительную ценность или полезность рассматриваемого параметра. Так, в табл. 17.4 физическое состояние офис­ного здания закодировано следующими категориями: «плохое», «удов­летворительное», «хорошее» и «отличное». На базе анализа рыночных данных можно численно идентифицировать относительную значимость указанных категорий физического состояния офисного здания, напри­мер: «плохое» (— 1,2); «удовлетворительное» (— 0,5); «хорошее» (0); «отлич­ное» (1). В данном случае числовая идентификация происходит по трем категориям: «плохое», «удовлетворительное» и «отличное», так как чис­ловое значение категории «хорошее» принято равным нулю.

Введение в модель скалярных переменных позволит сократить число независимых переменных и массив рыночных данных, необходимых для калибровки модели. Необходимо учитывать, что скалярные переменные для аддитивных моделей базируются вокруг их нулевого значения и вок­руг единицы — для мультипликативных моделей. Для повышения эф­фективности калибровки моделей возможно применение специальных математических преобразований для количественных параметров (пере­менных) объектов недвижимости:

• обратное (деление единицы на заданное число);

• экспоненциальное (возведение в степень заданного числа);

• логарифмическое (логарифмирование заданного числа).

Математические преобразования количественных переменных позво­ляют учитывать нелинейные зависимости в линейных «оценочных» мо­делях. Например, в линейной модели можно учесть нелинейное влияние изменения текущей доходности на стоимость доходной недвижимости.

Для выявления взаимного влияния количественных и качественных параметров объекта недвижимости используются также мультипликатив­ные преобразования независимых переменных. Например, современная внутренняя отделка офисного здания («евроремонт») может внести больший вклад в стоимость крупного здания высшей категории каче­ства, чем в стоимость небольшого по размерам здания низкой категорий. Такое взаимовлияние можно учесть в моделировании посредством муль­типликативных преобразований переменных в линейных моделях (пере­

 

умножение количественной и качественной переменных). Аналогично Проводят также дробное преобразование посредством деления одной пе­ременной на другую (например, средний размер комнат определяется делением площади на число комнат).

 

□ 17.3. Структура базовой «оценочной» модели и ее основные виды

 

Базовую оценочную модель можно представить следующим образом:

 

(17.1)

В условиях рыночного равновесия эту модель можно представить в несколько ином виде:

(17.2) (17.3)

 

Суммируя составные части модели (17.2), получаем:

 

Модель (17.3) линейна и аддитивна и свидетельствует о том, что стои­мость зданий (сооружений) можно определить отдельно от стоимости самого земельного участка и что стоимость каждого из компонентов стои­мости недвижимости прямо пропорциональна его размеру.

Если продолжить рассмотрение аддитивности стоимостных компо­нентов объекта недвижимости, то можно структурировать также стоимост здания (сооружения) V_h по отдельным к-м элементам V_b^k (фундаменты, Перекрытия, отделка и т.д.). Что касается «земельной составляющей» стои­мости недвижимости, то теоретически ее также можно структурировать поэлементно, но практически стоимость земельного участка (незастро­енного) всегда количественно зависит только от его площади либо от Фронтальной длины.

В таком виде оценочная модель с рыночных позиций отражает функ­цию предложения. С позиции функции спроса необходимо учесть по­-

лезность и качество того или иного объекта недвижимости, так как в зависимости от изменения этих категорий определяется и изменение его стоимости.

Введем в рассмотрение соответствующие качественные параметры, влияющие на стоимость объекта недвижимости: Q_i. - «внешний» i -й ка­чественный параметр (фактор времени, ссудный процент, уровень раз­вития социальной и инженерной инфраструктуры, стабильность и пред­сказуемость законодательных норм и т.д.); Q_j^b — качественный j -й пара­метр, определяющий полезность здания или сооружения (качество постройки, дизайн, физическое состояние, эффективный возраст и т. д.);

Q^l_f — качественный параметр земельного участка (форма и рельеф уча­стка, интенсивность транспортных потоков, экологическая эстетич­ность и т. п.). В структуру застройки каждого объекта недвижимости входит не только основное здание, но и дополнительные сооружения (например, склады, флигели, баня и др.). Обозначим эту дополнитель­ную стоимостную составляющую как V^h_{b + 1} Введенные дополнительные обозначения позволяют сформулировать общую оценочную модель:

 

Проиллюстрируем модель (17.4) на примере оценки загородных кот­теджей. При этом для компактного рассмотрения условного примера не­сколько упростим структуру этой модели:

 

 

 

Стоимость коттеджа v_b по определению равна произведению цены 1 м² полезной площади (v^b) на полезную площадь (S_b), а стоимость зе­мельного участка (V_i) равна произведению цены одной сотки земли (v^l) на площадь земельного участка (S_l). Тогда Q — коэффициент поправки на престижность и экологичность загородного микрорайона размещения оцениваемого коттеджа; Q_j^b — вектор качественных характеристик у кот­теджа (возраст, этажность, категория — строительный материал, водо­провод, газ, дизайн, отделка); Q _f^l — вектор качественных характеристик/ земельного участка (топография земельного участка, транспортная дос­тупность, наличие водоема для купания и леса для отдыха).

На основе анализа рыночных продаж и сметно-строительных расце­нок, сложившихся в рассматриваемом регионе, можно сформировать таб­-

 

лицы этих количественных и качественных показателей по оценивае­мым коттеджам (табл. 17.5).

 

Таблица 17.5

Количественные и качественные показатели л-го загородного коттеджа при массовой оценке (цифры условные)

 

Показатели (характеристики)	Значение показателей (характеристик)	Коэффициент калибровки модели
Плошадь земельного участка (Sl) Площадь (полезная) коттеджа {Sb)	20 соток 140 м^2	7500 руб./сотку 6250 руб./м^2
Возраст коттеджа (Q1^b)	5 лет
Состояние (Q2^b)	Хорошее	1,1
Этажность коттеджа (Q3^b)		1,05
Категория (класс) коттеджа (Q4^b)	Ниже среднего	0,8
Топография земельного участка (Q1^l)	Ровная	1,1
Транспортная доступность (Q2^l) Наличие водоема для купания и леса	Хорошая	1,2
для отдыха (Q3^l) Загородный микрорайон размещения коттеджа (Q1) Хозяйственный флигель (Vh + 1)	Есть Престижный и экологически благоприятный Есть	1,3 1,3 25000 руб.

 

Подставив значения табличных показателей для «-го загородного кот­теджа в модель (17.5), можно оценить его стоимость:

V= 1,3[ 1,05 * 1 * 0,8 * 1,1 * (6250 * 140) + 1,1 * 1,2 * 1,3 * (7500 * 20) + 25 000] = 1418 170 = 1420 тыс. руб.

Оценка стоимости n -го загородного коттеджа получена с учетом всех ее аддитивных составляющих и мультипликативных ее поправок. Такая оценка может быть проведена по всему множеству п оцениваемых заго­родных коттеджей. При необходимости оценщик дополнительно может корректировать все рассматриваемые коэффициенты калибровки моде­ли стоимости.

Эти коэффициенты не являются экзогенными параметрами модели, ю это эндогенные переменные, числовые значения которых «настраива­ем ются» в процессе моделирования и анализа полученных результатов моделирования.

В конечном счете результирующая модель оценки стоимости (в дан­ном случае п загородных коттеджей) должна быть деструктурирована, т. е. разложена на составляющие компоненты стоимости и представлена в виде набора таблиц, удобных для восприятия, в первую очередь - для налогоплательщика и других заинтересованных лиц.

 

 

Такие расчеты необходимы, так как владелец недвижимости должен понять, почему налогооблагаемая стоимость возросла, и четко увидеть влияние конкретного фактора на рост стоимости его собственности (на­пример, рост стоимости может произойти вследствие улучшения транс­портной доступности в результате реконструкции дорог и улучшения гра­фика работы общественного транспорта).

Общая оценочная модель (17.4) содержит как аддитивные, так и муль­типликативные компоненты. Характеристики, отражающие количествен­ные параметры, суммируются, а характеристики, связанные с качествен­ными параметрами, перемножаются. Иначе говоря, когда определены значения стоимости здания (сооружения), земельного участка и допол­нительных сооружений, итоговая сумма умножается на произведение «внешних» качественных параметров.

Сформулированную структуру общей оценочной модели следует рас­сматривать как базовую, на основе которой можно реконструировать бо­лее упрощенную структуру модели. Немаловажным обстоятельством в пользу такого упрощения является возможность проведения вычисли­тельных процедур. Иногда для модели (17.4) нельзя применять линей­ный и нелинейный множественный регрессионный анализ, поскольку компоненты этой модели не всегда полностью аддитивны и полностью мультипликативны. В этой связи можно использовать упрошенные струк­туры модели: аддитивную и мультипликативную. Эти структуры модели позволяют получать вполне удовлетворительные результаты.

Аддитивная структура модели при применении метода сравнения про­даж может быть представлена в следующей форме:

 

V = b₀+b_lX_l+b₂X₂+... + b„X_n, (17.6)

 

где V — расчетная рыночная стоимость недвижимости;

X₁, X₂, …, X_n — независимые переменные (общая площадь, число комнат, транс-
портная доступность и т.д.);
b_o — константа в денежном выражении:

b₁ , b₂, …, b_п — коэффициенты при независимых переменных (п - число неза­висимых переменных).

 

В этой модели рыночная стоимость недвижимости рассчитывается как совокупная величина, без ее дифференциации на компоненты сто­имости земельного участка и здания. Такая модель, обладая строго адди­тивной структурой, все же допускает введение мультипликативных и не­линейных переменных. Например, в качестве переменной можно выб­рать произведение общей жилой площади здания на показатель его качества, предполагая таким образом, что единица жилой площади в домах хорошего качества должна оцениваться выше, чем в домах среднего ка­чества. Пример учета нелинейной зависимости — квадратный корень от площади земельного участка. Можно воспользоваться целым рядом пре-

 

­образований параметров объектов недвижимости: перевод качественных параметров в бинарные и скалярные переменные, отражение нелиней­ных и совместных зависимостей количественных параметров с помощью обратных, экспоненциальных, логарифмических, мультипликативных и дробных преобразований. Все это позволяет использовать структуру адди­тивных оценочных моделей и получать удовлетворительные результаты.

Мультипликативная структура модели при применении метода срав­нения продаж может быть представлена в следующей форме:

 

 

В структуру модели (17.7) можно ввести мультипликативные соотно­шения, однако учет аддитивных компонентов и отдельное элиминирова­ние стоимости земельного участка и здания (сооружения) вызывают оп­ределенные трудности. Для преодоления этих трудностей следует ввести в модель соотношения, отражающие взаимосвязь земельного участка и здания (сооружения) посредством соответствующего коэффициента (от­ношения площади земельного участка к площади застройки).

Для решения модели (17.7) необходимы ее трансформация в адди­тивную форму посредством логарифмирования и затем применение ли­нейного множественного регрессионного анализа.

Модели, используемые при реализации метода сравнения продаж в массовой оценке недвижимости, могут быть аддитивными, мультипли­кативными и гибридными. Наиболее простые модели — аддитивные — могут найти широкое применение для оценки жилой недвижимости. В настоящее время рынок жилья уже сформировался, и в этой связи пред­ставляется возможным применение их оценочных моделей для массовой оценки этого типа недвижимости. Мультипликативные модели наиболее приемлемы для оценки офисных зданий, гостиниц, промышленных зда­ний и сооружений и т.п., а также незастроенных земельных участков (несельскохозяйственного использования). Что касается гибридных оце­ночных моделей, то по своему приложению к оценке недвижимости они универсальны. В то же время применение этих моделей связано с опре­деленными трудностями вычислительного порядка.

Модельный инструментарий при реализации доходного метода в мас­совой оценке недвижимости (доходной) ориентирован на восполнение недостаточной информации о доходах и расходах по объектам недвижи­мости. При этом оценочные модели строятся на базе имеющейся стати-

 

­стической информации, а результаты модельных расчетов (значения ти­пичных показателей) «распространяются» на весь массив объектов не­движимости. В качестве типичных показателей моделируются валовый доход, чистый доход, мультипликаторы (валовые рентные множители) и общие ставки капитализации. Эти типичные показатели доходной не­движимости определяются либо ее стратификацией, либо сравнением объектов недвижимости (поданным показателям) одного вида. При этом могут быть использованы не только электронные вычислительные таб­лицы, но и статистические модели, в частности, линейный множествен­ный регрессионный анализ.

При построении таких моделей в качестве зависимой переменной целесообразно выбирать некоторый удельный показатель (например, ва­ловый или чистый доход на единицу площади). Применение нормиро­ванной переменной позволяет исключить влияние на оценочную модель масштабного фактора недвижимости (ее размеров) и сосредоточить вни­мание на параметрах, наиболее существенно влияющих на удельный по­казатель: тип недвижимости, качество постройки, физическое состоя­ние, местоположение и т. п.

Моделирование мультипликатора валового дохода (отношение сто­имости объекта к величине валового дохода) ориентировано на выявле­ние совокупности факторов, определяющих взаимосвязь между стоимо­стью объекта и текущим доходом (плата за 1 руб. текущего дохода). К таким факторам относятся норма прибыли инвестора, или адекватная ставка дисконта, которая зависит от степени риска капиталовложений; прогнозный поток дохода (стабильный, возрастающий и снижающийся); ожидаемый срок поступления дохода; процент дохода, идущий на ком­пенсацию эксплуатационных расходов. Эти факторы с позиции модели­рования рыночной стоимости недвижимости можно представить соот­ветствующими характеристиками: местоположение, арендная площадь, физическое состояние, комфортность и т. д. Используя эти характери­стики, можно смоделировать мультипликатор валового дохода или вало­вый рентный множитель (GR). Например, мультипликативная модель для многоквартирного дома может иметь следующий вид:

 

 

 

 

Смоделировав индивидуальный мультипликатор валового дохода для рассматриваемого многоквартирного дома и установив значение валово­го дохода (произведение рыночной арендной платы за 1 м² жилой пло­шали на общую жилую площадь дома), можно определить его стоимость (произведение мультипликатора валового дохода на валовый доход). I Моделирование общей ставки капитализации исходит из анализа взаи-Шк мосвязей между чистым доходом и стоимостью объекта доходной W недвижимости.

Аддитивная модель общей ставки капитализации может быть пред­ставлена в следующем виде:

 

 

 

Переменная X_n+3 позволяет учитывать то обстоятельство, что объект недвижимости, имеющий фронтальную длину земельного участка боль­ше площади застройки, обеспечивает большую с позиции инвестора цен­ность. Переменная X_n+4 отражает возможность изменения величины R₀ в зависимости от размера здания доходной недвижимости.

Моделирование R₀ играет ключевую роль при расчете стоимости до­ходного объекта недвижимости при условии прогнозирования чистого Дохода от этого объекта. В конечном счете, если знать индивидуальную (по типу недвижимости, месторасположению, качеству застройки и т. п.) ставку общей капитализации для объекта недвижимости, то мож­но рассчитать его стоимость (по методу прямой капитализации).

Представленную выше структуру общей оценочной модели (17.4) также можно специфицировать при реализации затратного метода оценки не­движимости. Исходным этапом такой спецификации затратной оценоч­ной модели является стратификация множества рассматриваемых зда­ний и сооружений по однородным группам и базисным стоимостным характеристикам. Так, в отечественной оценочной практике базисом для определения стоимости строительства 1 м² общей жилой плошади домов разного типа служат ресурсно-технологические модели, разработанные

 

для характерных типов жилых домов в зависимости от основного мате­риала стен, этажности, объемно-планировочных решений и т.п.

Автоматизированный расчет восстановительной (замещающей) стои­мости здания (сооружения) можно осуществить:

• методом квадратных метров;

• поэлементным методом;

• методом количественного анализа.

Эти методы отличаются уровнем агрегации и детализации использу­емой в процедуре расчета информации. Третий метод, наиболее подроб­ный, требует большего массива нормативно-справочной информации и проектно-сметной документации.

Важной составляющей затратной оценочной модели является блок анализа износа зданий (сооружений). В Строительных нормах и прави­лах (СНиП) определены нормы физического износа по жилым и нежи­лым зданиям и сооружениям. Однако применение этих норм износа хотя в определенной мере и допустимо при массовой оценке недвижимости, но эти нормы не позволяют определить ее рыночную стоимость. Это нормы лишь физического износа и не отражают функцион&чьное и эко­номическое старение (моральный износ). При расчете износа в массовой оценке недвижимости также нельзя воспользоваться установленными в бухгалтерском учете нормами амортизации.

При проведении оценки недвижимости необходимо подходить к кате-'I гории «износ» как к категории рыночной, так как стоимость износа ' является производной от состояния рынка недвижимости. В этой свя­зи модели (функции) начисления износа должны быть рассчитаны на базе рыночных данных путем сравнения цен продаж (или прав аренды) сопоставимых объектов недвижимости с учетом элиминирования стои­мости земельных участков.

 

 

□ 17.4. Основные статистические характеристики

многомерного регрессионного анализа (МРА) в моделировании массовой оценки недвижимости

 

Эффективное применение оценщиком «оценочных» моделей во мно­гом предопределяется не только его глубокими профессиональными зна­ниями рынка недвижимости, но и владением аппарата МРА (линейного и нелинейного). Речь идет о возможности оценщика дать квалифициро­ванное заключение по результатам модельных расчетов стоимости не­движимости. А по существу дать определенный ответ: насколько модель­ная расчетная стоимость недвижимости адекватна объективно сложив-

шейся на рынке стоимости? С помощью категорий математической ста­тистики можно дать ответ на этот вопрос, проанализировав соответству­ющие статистические характеристики используемой «оценочной» моде­ли относительно ее адекватности объективной реальности. Например, можно использовать семь статистических характеристик, первые три из которых рассматриваются как мера согласия сформулированной модели, отражающая предикативную точность (истинность) используемых мате­матических зависимостей (уравнений). К ним относят коэффициент оп­ределенности (детерминации) (D¹), среднеквадратическую ошибку (а) и коэффициент вариации (С). Каждая из этих характеристик отражает степень адекватности используемых в модели статистических уравнений. Вторая группа статистических характеристик определяет статистическую значимость отдельных переменных моделей: коэффициент корреляции (г), критерии Стьюдента и Фишера и бета-коэффициент.

Коэффициент определенности (детерминации) (D²). По определению из любой регрессионной модели можно определить параметры (b₀, Ь_{, Ь_т) при соответствующих независимых переменных и остаточную дис­персию (отклонения). Последняя отражает вариацию переменных от их средних значений («остатки») «не объяснимых» данной регрессионной моделью. Тогда коэффициент определенности детерминации в контексте рассматриваемых «оценочных» моделей можно рассчитать по формуле

 

 

 

Таким образом, величина D² соответствует доле (проценту) цен, «объяс­нимых» регрессионной моделью. Этот коэффициент может принимать значения в интервале от 0 до 1. Когда D² = 0, никакая вариация (откло­нение от средней цены) цен «не объясняется» моделью. Наоборот, когда

D² = 1, все отклонения от средней цены «объясняются» уравнениями регрессии.

Среднеквадратическая ошибка модели (σ) измеряет величину откло­нения расчетных (прогнозных) цен продаж, получаемых из регрессион­ной модели, от фактически сложившихся цен продаж на рынке. Она определяется по формуле

 

 

Величина σ представляет собой меру среднеквадратической ошибки или дисперсию регрессионной модели. Извлечение квадратного корня позволяет получить значение такой ошибки, которую можно рассматри­вать как среднеквадратическое отклонение ошибок регрессионной моде­ли. В отличие от коэффициента D², который выражается в долях (в про­центах), σ измеряет отклонения (погрешность) в стоимостном выраже­нии. Существующее программное обеспечение регрессионного анализа позволяет вычислить не только значение σ, но и соответствующие дове­рительные интервалы для расчетной (модельной) стоимости по отдель­ным объектам недвижимости. Эта стоимость является функцией от σ и индивидуальных (количественных и качественных) параметров конкрет­ных объектов недвижимости. Чем ближе параметры объекта недвижимо­сти к параметрам типового объекта (их значения ближе к средним значе­ниям), тем меньше среднеквадратическая ошибка и доверительный ин­тервал расчетной (модельной) стоимости.

Коэффициент вариации (С_v) в регрессионном анализе определяется как отношение о к средней цене продажи (сделки):

 

С_v = * 100% (17.12)

Коэффициент С_v аналогичен показателю коэффициента вариации, используемого при анализе вариационного ряда и определяемого как отношение среднеквадратического отклонения цен продаж к средней цене. Если предположить, что рассчитанная среднеквадратическая ошибка по рассматриваемой регрессионной модели составила, например, 5000 у.е.. а средняя цена сделок с недвижимостью определена на уровне 50000 у.е., то коэффициент вариации будет равен (5000/50 000 100% = 10%). Это означает, что при нормальном распределении случайных величин (цен продаж на рынке недвижимости) примерно ²/₃ расчетных (модельных) цен из регрессионной модели находятся в пределах 10%-ных отклоне­ний от средних цен. Такой результат моделирования стоимости недви­жимости можно рассматривать как безусловно хороший.

Коэффициент корреляции (r) является одной из статистических ха­рактеристик, относящихся к анализу значимости отдельных переменных регрессионной модели. Он служит мерой линейной зависимости между двумя переменными, принимая значения в интервале от —1 до +1. При этом необходимо иметь в виду, что нулевое или близкое к нулю значение r не означает «отсутствие» зависимости (между двумя переменными), а лишь указывает на «отсутствие» линейной зависимости (может быть ещё и нелинейная зависимость).

Как правило, существующее компьютерное программное обеспече­ние позволяет рассчитать корреляционную матрицу коэффициентов кор­реляции между всеми парами переменных. При анализе корреляции той или иной независимой переменной с зависимой переменной следует иметь в виду, что коэффициент корреляции является безразмерной величиной или процентным отношением, отражающим наличие только линейной зависимости между двумя переменными. Например, рассчитаны два коэф­фициента корреляции, отражающие тесноту связи: между ценой и пло­щадью объекта недвижимости г = 0,92 и ценой и местоположением г = 0,62. Это позволяет лишь утверждать, что для рассматриваемых двух пар существует линейная зависимость и для первой пары (стоимость объекта недвижимости от его площади) эта зависимость более существенна для данного регионального рынка недвижимости.

Критерий Стьюдента (t - статистика) показывает меру значимости (или весомости) переменной регрессии на изменения зависимой переменной (цены сделки) и вычисляется как отношение соответствующего коэффи­циента регрессии (b) к его среднеквадратической ошибке (s_b):

t =│ │. (17.13)

 

Величина s_b характеризует среднеквадратическое отклонение коэф­фициента регрессии b и отражает погрешность при использовании этого коэффициента в качестве статистической характеристики связи незави­симой переменной X_i и зависимой переменной Р. В том случае, если значение t достаточно велико, то есть основание считать, что X_i является значимой переменной при расчете Р (цены продажи). Наоборот, если значение / мало, то можно предположить нулевое значение соответству­ющего коэффициента регрессии b_i, а также и несущественную значи­мость независимой переменной X_i для моделируемой цены продажи Р.

Для данного критерия имеется специальная таблица, по которой мож­но определить его значение исходя из числа степеней свободы (п — к — 1), где п — число переменных; к — количество независимых переменных. В общем случае, при достаточно большой статистической выборке (не менее 50 объектов недвижимости) значение t -статистики более ±2,00 сви­детельствует о существенной значимости соответствующей независимой переменной, так как при таком табличном значении t - распределения Стьюдента нулевая гипотеза о равенстве нулю коэффициента регрессии отвергается (считается значимым). Предположим, что для 60 сделок с недвижимостью (число степеней свободы равно 58) t - статистика для Независимой переменной — площадь объекта — определена на уровне 8,3. Табличное значение t - распределения Стьюдента для числа степеней свободы 58 равно ± 2,001, при котором с вероятностью 95% можно Утверждать, что коэффициент регрессии не равен нулю. Следовательно,

 

 

в данном случае при моделировании стоимости недвижимости площадь является существенной независимой переменной.

Критерий Фишера (F - статистика) связан с критерием Стьюдента и также используется для определения значимости независимых перемен­ных регрессионной модели. В МРА математическая зависимость крите­риев Стьюдента и Фишера определяется уравнением

F = t². (17.14)

 

Для определения этого критерия также имеются таблицы как в спе­циальной литературе, так и в учебниках по математической статистике. В общем случае при достаточно большой выборке табличное значение F -статистики, превышающее 4,0, указывает на то, что соответствующая независимая переменная значима при моделировании P (стоимости не­движимости) с вероятностью 95%.

Бета-коэффициенты представляют собой «нормированные» коэффи­циенты регрессии, являющиеся мерой значимости отдельных перемен­ных относительно друг друга. Бета-коэффициенты и коэффициенты рег­рессии связаны между собой следующим уравнением:

 

Бета-коэффициенты эффективны, если необходимо сравнить отно­сительную значимость независимых переменных. Допустим, например, что оценщику нужно определить, какая из двух переменных — площадь или эффективный возраст недвижимости — более значима для стоимо­сти объекта недвижимости. Поскольку площадь измеряется в квадрат­ных метрах, а эффективный возраст — в годах, коэффициенты регрессии нельзя сравнить непосредственно. Если обе переменные нормировать, то можно осуществить такое сравнение. Допустим, что бета-коэффиии-ент для площади равен 0,3, а для эффективного возраста — (-0,45). Это означает, что при постоянных значениях остальных независимых пере­менных регрессионной модели увеличение площади, например, на 10^е* вызовет увеличение стоимости недвижимости на 3%. Аналогично, уве­личение эффективного возраста на 10% снизит стоимость недвижимости на 4,5%. В данном случае эффективный возраст в большей степени влия­ет на изменение стоимости недвижимости, чем ее площадь.

Приведенные выше статистические характеристики в МРА можно рассматривать не только как оценочные параметры адекватности модели объективным реалиям, но и как инструмент калибровки модели посред­ством введения соответствующих корректировок. Существующее компь­ютерное программное обеспечение позволяет квалифицированному оцен-

 

 

­щику проводить такого рода «настройку» модели, работая в диалоговом режиме с компьютером.

Пример. Рассмотрим применение некоторых указанных выше стати­стических характеристик в МРА. Предположим, что с помощью компь­ютерной программы проведен регрессионный анализ рыночных данных по сделкам с жилой недвижимостью. Результаты этого анализа на п-м этапе моделирования распечатаны (или представлены на дисплее компь­ютера) в следующем виде (табл. 17.6).

Таблица 17.6

 

Результаты МРА рыночных данных по сделкам с жилой недвижимостью (цифры условные)