
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание местоположения объектаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Контрольные вопросы 1.Какие документы являются основанием для проведения оценки? 2.Какие макроэкономические показатели исследуются при формировании массива внешней информации? Какие источники информации могут быть использованы при сборе внешней информации? 3.Какую информацию о состоянии рынка недвижимости и смежных рынков необходимо проанализировать оценщику? Какие источники информации могут использоваться при этом? 4.Что представляет собой внутренняя информация? Каковы основные источники ее получения? 5.Какая внутренняя документация необходима для проведения оценки объекта недвижимости? 6.Каким образом электронные средства коммуникации могут быть использованы в процессе сбора информации? 7.Какие специализированные справочники и программные продукты могут быть использованы оценщиком в процессе оценки недвижимости? 8.Каковы основные цели и задачи оценщика при осмотре объекта оценки? Как обеспечить доступ оценщика на объект оценки? 9. Какую основную информацию необходимо изложить при описании объекта оценки в процессе
Тесты 1. Для определения объема необходимой информации следует: а) изучить договор об оценке и техническое задание на оценку; б) провести интервью с заказчиком и собственником; в) рассчитать предварительную стоимость объекта оценки; г) составить отчет об оценке; д) проанализировать макроэкономические показатели; е) проанализировать состояние рынка недвижимости; ж) провести осмотр и техническую экспертизу. 2. Сбор внешней информации предполагает: а) сбор данных о физических характеристиках объекта оценки; б) анализ политических и социальных факторов; в) анализ макроэкономических показателей; г) анализ общей конъюнктуры и перспектив развития рынка недвижимости
д)анализ внутренней документации объекта оценки; е)анализ затрат на строительство объекта оценки. 3. При анализе затрат на воспроизводство/замещение объекта оцен- а)«Справочник оценщика: Промышленные здания»; б)сборники укрупненных показателей восстановительной стоимости в)справочники Means, Marshal&Swift и другие зарубежные справоч- г)сметы строительства; д)программы правительства и прогнозы. 4. Из каких источников нельзя получить внутреннюю информацию а) интервью с заказчиком/собственником объекта оценки; б) интервью с представителем технической службы объекта оценки: в) исследования международных финансовых организаций; г) технический паспорт; д) осмотр и техническая экспертиза; е) учебные пособия и методические руководства по оценке. 5. При проведении оценки объекта недвижимости проведение осмотра а)обязательно лишь в исключительных случаях: б)обязательно; в)обязательно только в случае, когда заказчиком являются государ- г)не обязательно; д)обязательно, если заказчик/собственник не предоставляет подроб- 6. При осмотре объекта оценки необходимо провести его фотографи- а) верно; б) неверно. 7. При оценке объекта недвижимости дата оценки соответствует: а) дате составления отчета об оценке; б) дате подписания договора на оценку; в) дате составления технического задания на оценку; г) дате последнего осмотра объекта оценки; д) дате последнего капитального ремонта объекта оценки; е) последней отчетной дате (последней дате составления бухгалтерс- 8. При описании состояния объекта оценки для ориентировочной а) описание состояния несменяемых конструкций зданий; б) описание состояния внутренних конструктивных элементов; в) описание рынка недвижимости.
Временная оценка денежных потоков
Функция «сложный процент». Функция «дисконтирование». Функция «текущая стоимость аннуитета». Функция «периодический взнос на погашение кредита». Функция «будущая стоимость аннуитета». Функция «периодический взнос на накопление фонда». Взаимосвязи между различными функциями.
Принятие решения о вложении капитала определяется в конечном счете величиной дохода, который инвестор предполагает получить в будущем. Например, приобретая сейчас облигацию, мы рассчитываем в течение всего срока займа регулярно получать доход в виде начисленных процентов, а по окончании получить основную сумму долга. Вложение капитала выгодно только в том случае, если предполагаемые поступления превысят текущие расходы. В нашем примере инвестиционный доход равен сумме полученных процентов, однако положительные денежные потоки (выплата процентов и основной суммы долга) и отрицательные денежные потоки (инвестирование капитала) не будут совпадать по времени возникновения и, следовательно, будут несопоставимы. Временная теория стоимости денег исходит из предположения, что деньги, являясь специфическим товаром, со временем меняют свою стоимость и, как правило, обесцениваются. Изменение со временем стоимости денег происходит под влиянием целого ряда факторов. Важнейшими факторами можно назвать инфляцию и способность денег приносить доход при условии их разумного инвестирования в альтернативные проекты. Таким образом, в нашем примере мы должны сравнивать затраты на приобретение облигации с суммой предстоящих доходов, приведенных по стоимости к моменту инвестирования. Приведение денежных сумм, возникающих в разное время, к сопоставимому виду называется временной оценкой денежных потоков. Временная оценка денежных потоков основана на использовании шести Функций сложного процента. 1.Сложный процент. 2.Будущая стоимость аннуитета. 3.Периодический взнос в фонд накопления. 4.Дисконтирование. 5.Текущая стоимость аннуитета. 6.Периодический взнос в погашение кредита. Теория и практика использования указанных функций сложного процента базируется на ряде допущений. 1.Денежный поток — это денежные суммы, возникающие в определенной хронологической последовательности. 2.Денежный поток, в котором все суммы различаются по величине, называют обычным денежным потоком. 3.Денежный поток, в котором все суммы равновеликие, называют аннуитетом. 4.Суммы денежного потока возникают через одинаковые промежутки времени, называемые периодом. 5.Денежный поток может возникать в конце периода, а также в начале и середине периода. 6.Предварительно рассчитанные таблицы сложного процента без корректировки применимы только к денежному потоку, возникающему в конце периода. 7.Доход, получаемый на инвестированный капитал, из хозяйственного оборота не изымается, а присоединяется к основному капиталу. 8.Временная оценка денежных потоков учитывает риски, связанные с инвестированием. 9.Риск — это вероятность получения в будущем дохода, совпадающего с прогнозной величиной. 10.Уровень риска должен иметь адекватную ставку дохода на вложенный капитал. 11.Ставка дохода на инвестиции — это процентное соотношение между чистым доходом и вложенным капиталом. Для приведения денежных потоков к сопоставимому виду существуют так называемые множительные таблицы. В приложении 4 приведены два типа таблиц. Таблицы типа А систематизированы по видам функций сложного процента. Для их использования необходимо определить используемую функцию и на пересечении строки, соответствующей периоду, и колонки, адекватной ставке дисконта, найти множитель, позволяющий откорректировать ту или иную сумму. Таблицы типа Б сгруппированы по величине процентной ставки. Для решения задачи в этом случае необходимо сначала найти страницу, совпадающую со ставкой дисконта, а затем на пересечении колонки, совпадающей с нужной функцией, и строки, соответствующей периоду, найти множитель.
□ 5.1. Функция «сложный процент»
Символ функции - FV. Таблицы типа А - А-3. Таблицы типа Б - колонка 1. Данная функция позволяет определить будущую стоимость суммы, которой располагает инвестор в настоящий момент, исходя из предпола гаемой ставки дохода, срока накопления и периодичности начисления процентов.
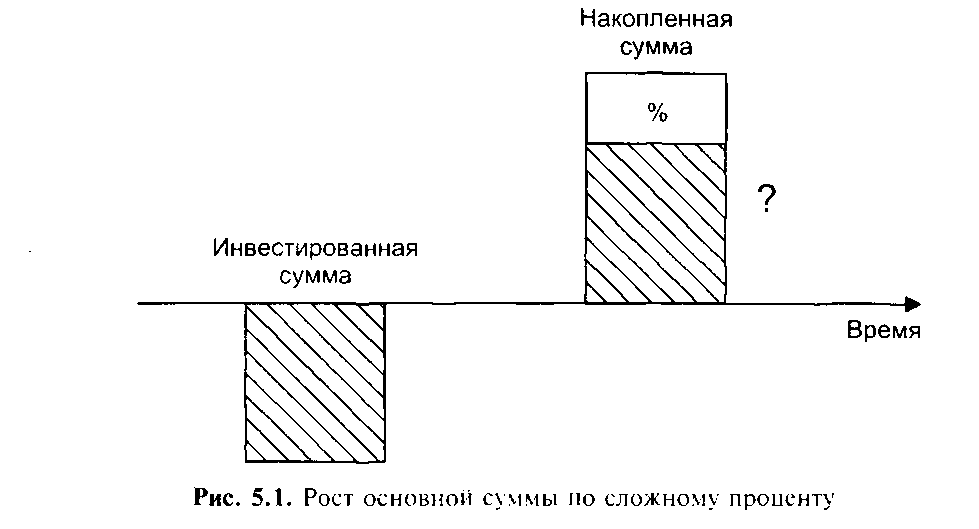
Расчет будущей стоимости основан на логике сложного процента (рис. 5.1), который представляет геометрическую зависимость между первоначальным вкладом, процентной ставкой и периодом накопления:
FV = S(1 + i)n, где FV — величина накопления; S — первоначальный вклад; i — процентная ставка; п - число периодов начисления процентов.
Задача, которая по сути является алгоритмом, позволяющим решать самые разнообразные инвестиционные вопросы, может быть сформулирована следующим образом
Какая сумма будет накоплена вкладчиком через три года, если первоначальный взнос составляет 400 тыс. руб., проценты начисляются ежегодно по ставке 10%?
Решение. Таблицы типа Б. 1)Найдем страницу, соответствующую процентной ставке 10%. 2)В колонке 1 найдем фактор, соответствующий периоду накопления. 3)Период накопления — 3, фактор — 1,3310. 4)Рассчитаем сумму накопления:
400[FV] = 400 • 1,3310 = 532,4 тыс. руб.
Таблицы типа А. 1.В табл. А-3 на пересечении колонки, соответствующей процентной ставке (10%), и строки, соответствующей периоду начисления процентов (3 года), найдем фактор — 1,3310. 2)Рассчитаем сумму накопления:
400[FV] = 400 • 1,3310 = 532,4 тыс. руб. (табл. 5.1).
Таблица 5.1 Процесс накопления в динамике
Таким образом, сложный процент предполагает начисление процентов не только на сумму первоначального взноса, но и на сумму процентов, накопленных к концу каждого периода. Это возможно только в случае реинвестирования суммы начисленных процентов, т.е. присоединения их к инвестиционному капиталу. Техника простого процента предполагает арифметическую зависимость между суммой вклада, процентной ставкой и периодом накопления. Следовательно, простой процент начисляется только один раз в конце срока депозитного договора. Если бы приведенная выше ситуация предполагала начисление простого процента, то накопленная сумма составила: 400(1 + 0,10 * 3) = 520 тыс. руб. Периодичность начисления процентов влияет на величину накопления. Если вклад в сумме 100 тыс. руб. хранить два года в банке, начисляющем 24% годовых, то в зависимости от части начисления процентов, накопленная сумма составит: а) ежегодное начисление процентов — 1000[FV] = 1000 * 1,5376 = 1537,6;
б)полугодовое начисление процентов - 1000[FV] = 1000 *1,5735 = 1573,5; в)ежеквартальное начисление процентов — 1000[FV] = 1000 *1.5938 = 1593,8; г)ежемесячное начисление процентов - 1000[FV] = 1000 *1,6084 = 1608,4. Следовательно, чем чаще начисляются проценты, тем больше накопленная сумма. При более частом накоплении необходимо откорректировать процентную ставку и число периодов начисления процентов:
Число периодов = число периодов начисления в год * Число лет накопления
Для определения периода времени, необходимого для удвоения первоначального вклада, используется правило 72-х. Это правило дает наиболее точные результаты, если процентная ставка находится в интервале 3-18 %. Удвоение первоначального вклада произойдет через число периодов, равное частному от деления 72 на процентную ставку соответствующего периода. Пример. Если годовая ставка 24% и начисление процентов осуществляется ежегодно, удвоение произойдет через три года (72: 24).
□ 5.2. Функция «дисконтирование»
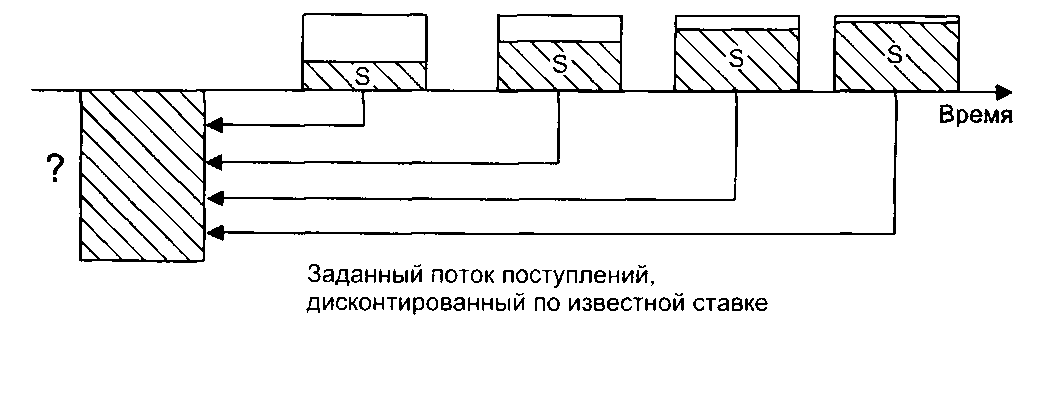
Символ функции - PV. Таблицы типа А - табл. А-1. Таблицы типа Б - колонка 4. Функция дисконтирования (рис. 5.2) позволяет определить настоящую стоимость суммы, если известна ее величина в будущем при данных периоде накопления и процентной ставке. Настоящая стоимость, а также текущая или приведенная стоимость являются синонимичными понятиями.
Задача-алгоритм
Какую сумму необходимо поместить на депозит под 10% годовых, чтобы через пять лет накопить 1500 тыс. руб.?
Решение. Таблицы типа Б. 1.Находим таблицу, соответствующую процентной ставке 10%. 2.В колонке 4 найдем фактор, исходя из периода дисконтирования в 5 лет - 0,6209. 3. Рассчитаем сумму вклада: 1500[PV] = 1500 • 0,6209 = 931.4 тыс. руб. Таблицы типа А. 1.Ha пересечении колонки, соответствующей процентной ставке (10%), и периода дисконтирования находим фактор — 0,6209. 2.Рассчитаем сумму вклада: 1500[PV] = 1500 • 0, 6209 = 931,4 тыс. руб. Таким образом, инвестирование 931,4 тыс. руб. на пять лет при ставке дохода 12% обеспечит накопление в сумме 1500 тыс. руб. Формула дисконтирования такова:
где PV — текущая стоимость; S — известная в будущем сумма; i — процентная ставка; п — число периодов начисления процентов.
Функция дисконтирования является обратной по отношению к функции сложного процента.
□ 5.3. Функция «текущая стоимость аннуитета»
Символ функции — PVA. Таблицы типа А - А-2. Таблицы типа Б — колонка 5. Аннуитет - это денежный поток, в котором все суммы возникают не только через одинаковые промежутки времени, но и равновеликие. Таким образом, аннуитет — это денежный поток, представленный одинаковыми суммами. Аннуитет (рис. 5.3) может быть исходящим денежным потоком по отношению к инвестору (например, осуществление периодических равных платежей) либо входящим денежным потоком (например, поступление арендной платы, которая обычно устанавливается одинаковой фиксированной суммой).
Рис. 5.3. Текущая стоимость аннуитета Задача-алгоритм. Какую сумму необходимо положить на депозит под 10% годовых, чтобы затем пять раз снять по 300 тыс. руб.?
Решение. Таблицы типа Б. 1.Находим страницу, соответствующую процентной ставке 10%. 2.Находим фактор текущей стоимости аннуитета в колонке 5 и строке, соответствующей периоду существования аннуитета, — 3,7908. 3.Рассчитаем текущую стоимость аннуитета: 300[РVА] = 300 * 3,7908 = 1137 тыс. руб.
Таким образом, инвестор снимает со счета пять раз по 300 тыс. руб., или 1500 тыс. руб. Разница между первоначальным вкладом 1137 тыс. руб. и накоплением 1500 тыс. руб. обеспечивается суммой процентов, начисляемых на уменьшающийся остаток вклада по технике сложного процента. Этот процесс предполагает в конечном счете нулевой остаток на депозите. Проверим данное утверждение методом «депозитной книжки» (табл. 5.2). Вклад в 1137 тыс. руб. позволит пять раз в конце года снять 300 тыс. руб., если банк начисляет 10% годовых. Таблица 5.2 Метод депозитной книжки
Предыдущие рассуждения основывались на предположении, что аннуитет возникает в конце периода. Такой аннуитет называется обычным и графически он может быть представлен следующим образом.
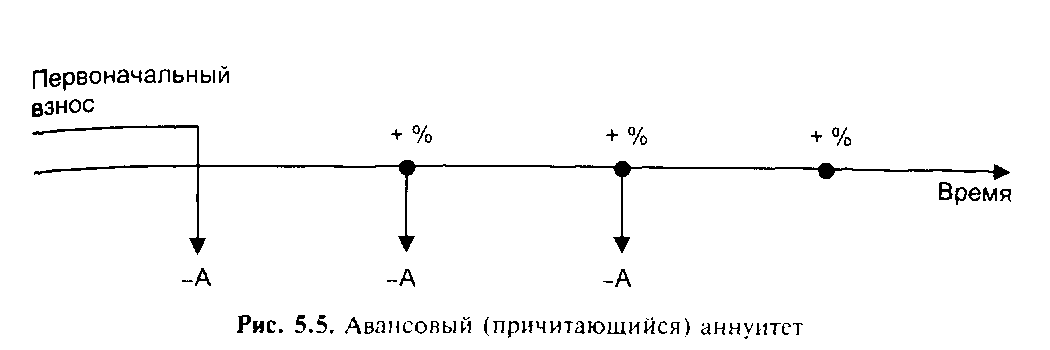
Однако на практике возможна ситуация, когда первый платеж произойдет одновременно с начальным поступлением. В последующем аннуитеты будут возникать через равные интервалы. Такой аннуитет называется авансовым или причитающимся аннуитетом. Для того чтобы определить текущую стоимость авансового аннуитета, необходимо проследить движение денежного потока. Поскольку первый аннуитет по времени совпадает с депонированием основного вклада, его не следует дисконтировать. Все последующие аннуитеты дисконтируются в обычном порядке, однако период дисконтирования всегда
будет на единицу меньше, следовательно, фактор текущей стоимости авансового аннуитета соответствует фактору обычного аннуитета для предыдущего периода, к которому добавлена единица. Эта добавленная единица обеспечивает заданный поток аннуитета.
Фактор текущей стоимости авансового аннуитета = Кп - 1 + 1,0. Например, фактор текущей стоимости авансового аннуитета, возникающего семь раз при ставке дисконта 12%, определяется следующим образом. 1.Определим фактор текущей стоимости аннуитета для периода: 7-1 = 6, ставка дисконта 12%. В колонке 4 находим его значение -4.1Н4. 2.Рассчитаем фактор текущей стоимости авансового аннуитета для заданного потока: 4,1114 + 1,0 = 5,1114. Оценка инвестиционной привлекательности требует в ряде случаев дифференциации ставок дисконта в зависимости от уровня риска тех или иных операций. Учет различий в уровне неопределенности требует от аналитика применения соответствующих ставок дисконта. Пример. Владелец кафе предполагает в течение шести лет получать ежегодный доход от аренды в сумме 60 млн руб. В конце шестого года кафе будет продано за 1350 млн руб., расходы по ликвидации составят 5% продажной цены. Прогнозирование доходов от аренды имеет большую степень вероятности, чем возможность продажи объекта за указанную цену. Различия в уровне риска определяют выбранные аналитиком ставки дисконта для дохода от аренды и продажи: 8% и 20% соответственно. Решение. 1.Рассчитаем текущую стоимость потока доходов от аренды: 60[PVA] = 60 * 4,6229 = 277.4 млн руб. 2.Определим текущую стоимость дохода от продажи: 1350(1 - 0.05) [РV] = 1282,5 • 0.3349 = 429.5 млн руб. 3.Рассчитаем сумму доходов: 277,4 + 429,5 = 706.9 млн руб. Меняющаяся конъюнктура рынка, усовершенствование эксплуатационных характеристик объекта, инфляция и многие другие факторы оказывают существенное влияние на величину ежегодного дохода. Определение текущей стоимости меняющейся суммы потока доходов требует определенных навыков работы с коэффициентами, приведенными в колонке 5. Пример. Аренда магазина принесет его владельцу в течение первых трех лет ежегодный доход в 750 млн руб., в последующие пять лет дох составит 950 млн руб. в год. Необходимо определить текущую стоимость совокупного дохода, если ставка дисконта 10%. Решение. Данная задача имеет несколько вариантов решения, суть которых проиллюстрирована рис. 5.6 - 5.8.
В данном случае (рис. 5.6) текущая стоимость совокупного дохода равна текущей стоимости потока доходов в 750 млн руб. за первые три года и потока доходов в 950 млн руб. за последующие пять лет. 1. Рассчитаем текущую стоимость арендных платежей за первые три 750[PVA] = 750 * 2,4869 = 1865,2 млн руб. 2. Определим текущую стоимость арендной платы за последующие 950 [PVA] = 950(5,3349 - 2,4869) = 2705,6 млн руб.
3. Суммарная текущая стоимость арендной платы 1865.2 + 2705,7 = = 4570,8 млн руб.
Текущая стоимость суммарного потока доходов, как видно из рис. 5.7, равна разности потока доходов в 950 млн руб., полученного за все восемь лет, и несуществующего потока доходов в 200 млн руб. (950—750) за первые три года. Решение. 1. Рассчитаем текущую стоимость дохода от аренды исходя из пред- 950[РVА] = 950 5,3349 - 5068,2 млн руб. 2. Вычислим текущую стоимость завышенной суммы аренды, кото- (950 - 750) \PVA\ = 200 * 2,4869 = 497,4 млн руб.
Текущая стоимость арендной платы за восемь лет составляет 5068,2 — - 497,4 = 4570,8 млн руб.
Третий вариант решения (рис. 5.8) предполагает, что текущая стоимость совокупного дохода равна сумме дохода в 750 млн руб. за восемь лет и превышения дохода в 200 млн руб., достигнутого в последние пять лет аренды.
Решение. 1.Рассчитаем текущую стоимость доходов от аренды в 750 тыс. руб. 750[РК4] = 750 * 5,3349 = 4001,2 млн руб. 2.Вычислим текущую стоимость дополнительного дохода от аренды, (950 - 750) [PVA] = 200 * (5,3349 - 2,4869) = 569,6 млн руб. 3.Текущая стоимость полученной арендной платы: 4001,2 + 569,6 = 5470,8 млн руб. Если полученные результаты имеют некоторые расхождения, то это является следствием округлений, допускаемых при расчетах.
□ 5.4. Функция «периодический взнос на погашение кредита»
Таблицы типа А — табл. А-2, фактор используется как делитель. Таблицы типа Б — колонка 6. Временная оценка денежных потоков может поставить перед аналитиком проблему определения величины самого аннуитета (рис. 5.9), если известны его текущая стоимость, число взносов и ставка дохода.
Задача-алгоритм. Какую сумму можно ежегодно снимать со счета в течение пяти лет, если первоначальный вклад равен 1500 тыс. руб.? Банк начисляет ежегодно 14 % при условии, что снимаемые суммы будут одинаковы.
Решение. Таблицы типа Б. 1. Находим фактор взноса на погашение кредита при условии, что 2. Рассчитаем величину аннуитета:
Таблицы типа А. 1. Находим в табл. А-2 фактор текущей стоимости аннуитета, возни- 2. Рассчитаем величину аннуитета:
Таким образом, если положить на счет под 14% годовых 1500 тыс. руб., можно пять раз в конце года снять по 437 тыс. руб. Дополнительно полученные деньги в сумме 685 тыс. руб. 1(437 * 5) — 1500] являются результатом начисления процентов на уменьшающийся остаток вклада. Функция «периодический взнос на погашение кредита» является обратной по отношению к функции «текущая стоимость аннуитета». Если:
Текущая стоимость = Аннуитет * Фактор текущей стоимости аннуитета аннуитета
то определение величины аннуитета при помощи фактора текущей стоимости аннуитета (колонка 5) возможно по формуле
Аннуитет = Текущая стоимость аннуитета *
Аннуитет (по определению) может быть как поступлением (входящим денежным потоком), так и платежом (исходящим денежным потоком) по отношению к инвестору. Поэтому данная функция может использоваться в случае необходимости расчета величины равновеликого взноса на погашение кредита при известном числе взносов и заданной процентной ставке. Такой кредит называют самоамортизирующимся. Пример. Рассчитаем величину ежегодного взноса в погашение кредита в сумме 40000 тыс. руб., предоставленного на 15 лет под 20% годовых. Решение. 1.Определим фактор периодического взноса на погашение кредита, если ставка - 20%, а число взносов - 15 (колонка 6) - 0,2139. 2.Рассчитаем величину взноса: 40000 [ Заемщик уплатит кредитору за 15 лет 128329,3 тыс. руб. (8555,3 * 15), что превышает величину выданного кредита на 88329,3 тыс. pv6. (128329,3 -- 40000). Разница является суммой процентов, уплаченных заемщиком за весь период кредитования, при условии, что основной долг постоянно уменьшается.
□ 5.5. Функция «будущая стоимость аннуитета»
Символ функции — FVA. Таблицы типа А — табл. А-4. Таблицы типа Б — колонка 2. Данная функция позволяет рассчитать величину накопленных равновеликих взносов при заданной ставке дохода (рис. 5.10).
Задача-алгоритм. Какая сумма будет накоплена на счете, если в течение четырех лет ежегодно вносить 350 тыс. руб., а банк начисляет на вклад 6% годовых?
Решение. Таблицы типа Б. 1. Определим фактор будущей стоимости аннуитета за четыре пери- 2. Рассчитаем величину накопления:
350 [FVA] = 350 * 4,3746 =1531 тыс. руб.
Таблицы типа А. 1. В табл. А-4 на пересечении колонки 6% и строки четвертого периода 2. Рассчитаем величину накопления: 350[PVA] = 350 • 4,3746 = 1531 тыс. руб. Таким образом, депонирование 1400 тыс. руб. (350 • 4) обеспечивает накопление в сумме 1531 тыс. руб. Разница представляет величину процентов, начисленных на возрастающую сумму вклада по технике сложного процента. Рассмотрим процесс накопления в динамике: 1. Первоначальный взнос — 350. 2. Процент за 1-й период — 0. 3. Накоплено — 350. 4. Процент за 2-й период — 21. 5. Второй взнос — 350. 6. Накоплено — 721. 7.Процент за 3-й период — 43. 8.Третий взнос - 350. 9.Накоплено - 1114. 10.Процент за 4-й период — 67. 11.Четвертый взнос — 350. 12.Накоплено - 1351.
□ 5.6. Функция «периодический взнос на накопление фонда»
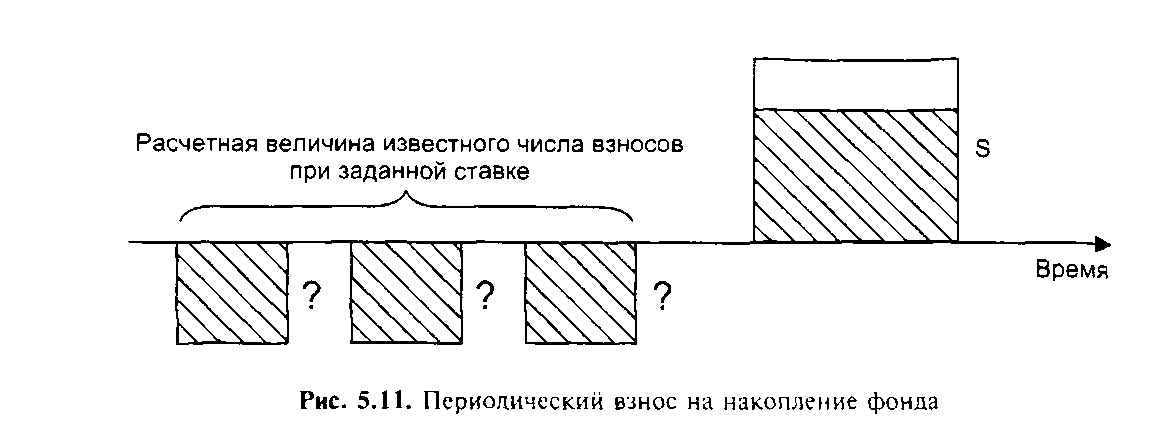
L-имвол функции — Таблицы типа А — табл. А-4. Фактор используется как делитель. Таблицы типа Б — колонка 3. Данная функция позволяет рассчитать величину периодически депонируемой суммы, необходимой для накопления нужной стоимости, при заданной ставке процента (рис. 5.11).
Задача-алгоритм.
Какую сумму необходимо пять раз внести на пополняемый депозит под 8% годовых, чтобы накопить 1700 тыс. руб.?
Решение. Таблицы типа Б. 1.Находим фактор периодического пятикратного взноса при 8%-ной ставке (колонка 3) — 0,1705. 2.Рассчитаем величину депозита:
1700[
Таким образом, суммарный взнос в 1540 (290 5) тыс. руб. при начислении 8% годовых позволит накопить 1700 руб. Таблицы типа А. 1.Определим фактор будущей стоимости аннуитета при ставке слож- 2.Рассчитаем величину депозита:
1700 *
Функция «периодический взнос на накопление фонда» является обратной по отношению к функции «будущая стоимость аннуитета». □ 5.7. Взаимосвязи между различными функциями
Расчет факторов шести функций основан на использовании базовой формулы сложного процента. Главным условием, обеспечивающим математическую взаимосвязь между функциями, является предположение, что начисленный процент не снимается с депозитного счета, а капитализируется. Таблица 5.3 Взаимосвязь функций
Использование таблиц требует четкого понимания экономической сущности функции. При решении различных проблем, возникающих в процессе оценки недвижимости, аналитик должен сформулировать ответы на ряд вопросов: • правильно ли применение конкретной функции? • необходимы ли комбинации функций? • необходимы ли корректировки процентной ставки и периодов в зависимости от частоты начисления процентов? • учтена ли конструкция денежного потока, т.е. возможность его возникновения в начале или конце периода?
Выводы
Временная оценка денежных потоков необходима для объективного сопоставления денежных сумм, возникающих в различное время. В основе временной оценки лежат шесть функций сложного процента. 1.Сложный процент. 2.Дисконтирование 3.Текущая стоимость аннуитета. 4.Периодический взнос в погашение кредита.
5. Будущая стоимость аннуитета. 6. Периодический взнос на накопление фонда. Сложный процент (базовая функция сложного процента) позволяет определить будущую стоимость при заданных периоде, процентной ставке и текущем взносе. Дисконтирование позволяет рассчитать настоящую (приведенную) стоимость при заданных периоде, процентной ставке и известной сумме в будущем. Текущая стоимость аннуитета дает возможность определить текущую стоимость взноса, обеспечивающего в будущем получение заданных равновеликих поступлений при известных числе периодов и процентной ставке. Периодический взнос в погашение кредита позволяет вычислить величину аннуитета при заданных текущей стоимости аннуитета, процентной ставке и периоде. Будущая стоимость аннуитета позволяет определить будущую стоимость периодических равновеликих взносов при заданных величине аннуитета, процентной ставке и периоде. Периодический взнос в накопление фонда позволяет рассчитать величину равновеликих взносов при заданных будущей стоимости, процентной ставке и периоде.
Контрольные вопросы и задания
1. Какая функция позволяет определить стоимость будущего дохода а) сложный процент; б) будущая стоимость аннуитета; в) периодический взнос на накопление фонда; г) дисконтирование; д) текущая стоимость аннуитета; е) периодический взнос на погашение кредита. 2. Какая функция позволяет определить размер периодического рав- а) сложный процент; б) будущая стоимость аннуитета;
в) периодический взнос на накопление фонда; г) дисконтирование; д) текущая стоимость аннуитета; е) периодический взнос на погашение кредита. 3. Какая функция позволяет определить стоимость накопления изве- а) сложный процент; б) будущая стоимость аннуитета; в) периодический взнос на накопление фонда; г) дисконтирование; д) текущая стоимость аннуитета; е) периодический взнос на погашение кре
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.018 с.) |










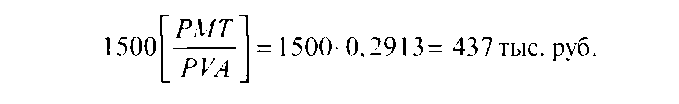


 ] = 40000 * 0,2139 = 8555,3 тыс.руб.
] = 40000 * 0,2139 = 8555,3 тыс.руб.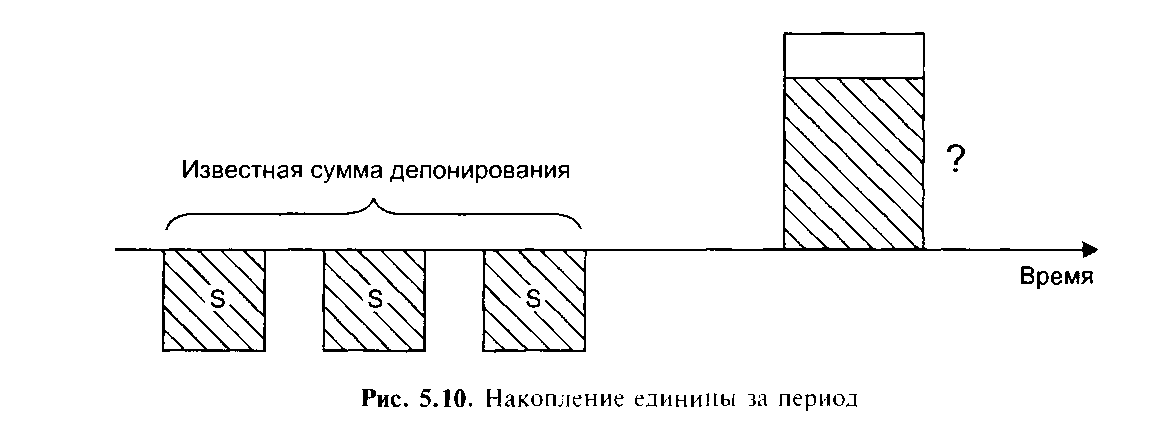

 = 290 тыс. руб.
= 290 тыс. руб.


