Особенности нелинейных систем

Нелинейные элементы в автоматических системах, как уже сказано, могут быть подразделены на две основные группы:

· естественные – непосредственно присутствующие в системе;

· искусственные – специально вводимые в систему для придания ей нужных свойств.

К первой группе относятся нелинейности типа «насыщение» (рис. 5.1, а), «зона нечувствительности» (рис. 5.1, б), «петля гистерезиса» (рис. 5.1, в). Нелинейность типа «насыщение» характерна для усилителей: при больших значениях входного сигнала выходной сигнал ограничен из-за недостатка мощности источника, питающего усилитель.

x

x

x

x

x

x

y

y

y

Рис. 5.1 – Типовые нелинейности:
а – насыщение; б – зона нечувствительности; в – гистерезис

«Зона нечувствительности» возникает в усилителях или датчиках, которые не реагируют на малые входные сигналы. Люфт – следствие зазоров в механических передачах.

y

y

y

Ко второй группе (искусственные нелинейности) относятся релейные характеристики (рис. 5.2): идеальное реле (рис. 5.2, а), реле с зоной нечувствительности (рис. 5.2, б), реле с гистерезисом (рис. 5.2, в), а также специальные (с кусочно-линейной характеристикой, с криволинейной характеристикой любого очертания и т. д.).

 

а б в

Рис. 5.2 – Искусственные нелинейности: а – идеальное реле;
б – реле с зоной нечувствительности; в – реле с гистерезисом

Различают статические и динамические нелинейности. Первые представляются в виде нелинейных статических характеристик, т. е. характеризуют нелинейную связь между установившимися значениями выхода и входа, а вторые описываются нелинейными дифференциальными уравнениями, когда выход нелинейно зависит не только от входного сигнала, но и от скорости его изменения или высших производных (пример – вязкое трение).

Исследовать нелинейную систему, как правило, значительно сложнее, чем линейную. Обычно линеаризуют звенья с несущественными нелинейностями и предельно упрощают уравнения существенно нелинейных звеньев.

Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма важных особенностей, отличающих их от линейных систем.

- Не выполняется принцип суперпозиции. В общем случае не существует правил преобразования структурных схем, подобных используемым в линейных системах.

- Не существуют общие методы решения нелинейных дифференциальных уравнений; исследование нелинейных систем носит качественный, приближенный характер.

- Нелинейная система может иметь несколько положений равновесия, в отличие от линейной системы, имеющей единственное положение равновесия. Если линейная система находится не на границе устойчивости, то при любых начальных условиях движение асимптотически затухает к положению равновесия (система устойчива в целом) или расходится (система не устойчива). Реальные (нелинейные) динамические системы могут иметь несколько положений равновесия, например, у математического маятника их бесконечное счетное множество j = k p; k = 0, ±1, ±2,....

- Переходные процессы в нелинейных системах имеют конечную длительность во времени, в отличие от линейных систем, где они теоретически бесконечны.

- Реальные значения переменных, описывающих нелинейные процессы, всегда ограничены энергетическими, материальными, прочностными ресурсами, даже в случае неустойчивости системы. Значения переменных неустойчивой линейной системы неограниченно растут во времени.

- Характер движения в нелинейной системе зависит от начальных условий и уровня воздействий. В реальных системах не выполняется принцип суперпозиции (при сложении воздействий реакция не равна сумме реакций на отдельные воздействия).

Из-за этих особенностей исследование нелинейных систем, в том числе устойчивости, становится более сложным. Кроме структуры нелинейной системы и значений ее параметров для устойчивости того или иного установившегося процесса имеют значение (в отличие от линейных систем) также и начальные условия. Кроме того, на устойчивость нелинейных систем может существенно влиять величина и вид внешних воздействий. Возможен новый вид установившегося процесса – автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий.

В общем случае на плоскости параметров нелинейной системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше (рис. 5.3):

Рис. 5.3. Возможные процессы в нелинейных системах:

а – устойчивые автоколебания; б, в – устойчивость в малом и неустойчивость в большом; г – устойчивые и неустойчивые автоколебания

· область устойчивости равновесного состояния с постоянным значением регулируемой величины;

· область устойчивых автоколебаний;

· область неустойчивости системы;

· области, соответствующие другим, более сложным вариантам поведения.

Если процессы в системе имеют вид, указанный на рис. 5.3, а, то равновесное состояние (х = 0) неустойчиво. В том случае, когда оба указанных на рис. 5.3, а колебания в переходных процессах стремятся к одной и той же амплитуде и к одной и той же частоте, система будет обладать устойчивыми автоколебаниями с амплитудой а.

На рис. 5.3, б, в показаны случаи, когда равновесное состояние
(х = 0) системы устойчиво «в малом» (при начальных условиях, не выводящих отклонения в переходном процессе за величину а), и неустойчиво «в большом» (при начальных условиях, выводящих отклонение в переходном процессе за пределы величины а).

На рис. 5.3, г показан случай трех возможных установившихся состояний: равновесное состояние (х = 0); колебания с постоянной амплитудой a ₁; колебания с постоянной амплитудой a ₂. Отметим, что колебания с амплитудой a ₁ неустойчивы. Система устойчива «в малом» по отношению к равновесному состоянию х = 0, а «в большом» наблюдаются устойчивые автоколебания с амплитудой a ₂.

Для иллюстрации особенностей нелинейной системы рассмотрим пример.

Пример. Автоколебания в релейной системе автоматического регулирования скорости вращения двигателя.

Считаем, что используемый датчик скорости имеет релейную характеристику с гистерезисом (рис. 5.4).

Составим математическую модель системы и будем использовать для решения «метод сшивания траекторий» или «метод припасовывания».

 

Рис. 5.4. Датчик с релейной характеристикой с гистерезисом

Предположим для определенности, что в исходном состоянии
(t = 0) отклонение скорости w вращения двигателя от требуемого значения w₀ составляет Dw(0) = D >d.

1-ый этап: Dw > d, u = – u ₀ (участок 3, 4)

Переключение на другую траекторию происходит при t = t ₁, когда Dw(t ₁) = –d.

Момент переключения определяем следующим образом:

2-ой этап: –d < Dw < d, u = + u ₀ (участок 1, 2)

Переключение происходит при t = t ₂, когда Dw(t ₂) = d.

Если обозначить t = t ₁ + t, где t – время после начала 2-го этапа, то

 

3-ий этап. Начинается в момент времени t = t ₂, когда отклонение скорости двигателя Dw(t ₂) достигло d. Поэтому, как и на 1-ом этапе, «двигаемся» по участку 4:

4-ый этап. Начинается в момент времени t = t ₃, когда отклонение скорости двигателя Dw(t ₂) достигло –d. Поэтому, как и на 2-ом этапе, «двигаемся» по участку 2:

Если обозначить t = t ₃ + t, где t – время после начала 4-го этапа, то

Выражения для Dw(t) на 2-ом и 4-ом этапах идентичны. Дальше все будет повторяться. Следовательно, в системе наблюдаются автоколебания (рис. 5.5).

t

t4

t2

Рис. 5.5 – Автоколебания

Амплитуда автоколебаний равна d, т. е. определяется шириной петли гистерезиса. Период колебаний равен T _a = t ₃ – t _1.

Метод фазового пространства

Рассматривается математическая модель нелинейной автономной системы (время t явно в уравнения не входит) в форме дифференциальных уравнений первого порядка, разрешенных относительно производных (форма Коши):

(5.1)

Состояние системы (5.1) характеризуется вектором . Начальное состояние х (0) автономной системы полностью определяет ее поведение для t > 0 независимо от того, каким путем система пришла в это состояние. Геометрическое место точек конца вектора х (t) при t ³ 0 образует траекторию состояния ― образ поведения при конкретном начальном состоянии. Совокупность фазовых траекторий называется фазовым портретом динамической системы.

Хотя геометрическая интерпретация метода пространства состояний распространяется на системы любого порядка, важное его преимущество ― наглядность ― наиболее ярко проявляется для систем 2-го порядка, когда состояния системы представляются точками на фазовой плоскости. Метод фазовой плоскости используется для предварительного качественного анализа общих закономерностей системы по ее упрощенным моделям.

Фазовая плоскость

Пусть заданы уравнения системы второго порядка

(5.2)

Фазовую траекторию в этом случае можно получить путем деления второго уравнения системы (5.2) на первое

(5.3)

и решения полученного дифференциального уравнения 1-го порядка при конкретных начальных условиях.

Если функции f ₁ и f ₂ однозначны, то каждой точке (х ₁, х ₂) соответствует единственное значение производной dx ₂/ dx ₁ (наклона касательной к фазовой траектории), т. е. через эту точку фазовой плоскости проходит только одна фазовая траектория. Единственность нарушается в так называемых особых точках, соответствующих состояниям равновесия системы

(5.4)

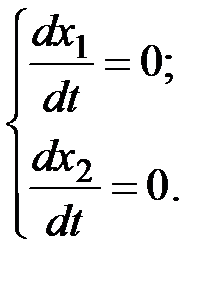
Координаты особых точек определяются из уравнений

(5.5)

В особых точках имеется неопределенность производной dx ₂/ dx ₁ = 0/0. Каждая особая точка изображает отдельное (тривиальное) решение системы (5.2) и должна рассматриваться как отдельная фазовая траектория.

В качестве фазовой переменной x ₁ часто выбирается переменная входа нелинейного элемента, а в качестве x ₂ – ее производная. В этом случае система уравнений (5.2) принимает вид:

(5.6)

(5.7)

и вместо (5.3) имеем:

Тот факт, что х ₂ = dх ₁/ dt, придает фазовой плоскости следующие свойства:

· особые точки располагаются только на оси абсцисс, где
х ₂ = dх ₁/ dt = 0;

· в верхней полуплоскости (х ₂ = dх ₁/ dt > 0) фазовые траектории направлены слева направо, т. е. в сторону увеличения х ₁, а в нижней полуплоскости ― справа налево;

· фазовые траектории ортогональны оси абсцисс, так как при х ₂ = 0 имеем dх ₂/ dх ₁ = ¥.

Виды особых точек

Рассмотрим особую точку – решение системы уравнений (5.4). Пусть функции f ₁ и f ₂ в окрестности этой точки допускают разложение в степенной ряд по отклонениям переменных (D х ₁, D х ₂). Тогда вместо нелинейных уравнений (5.2) можно получить систему линейных дифференциальных уравнений для малых отклонений переменных, которая в матричной форме примет вид:

(5.8)

A – матрица Якоби системы (5.2) в рассматриваемой точке равновесия.

Решения уравнений (5.8) имеет вид:

(5.9)

(5.10)

где постоянные зависят от начальных условий D х ₁(0), D х ₂(0) и корней характеристического полинома

Рассмотрим типы особых точек линейных систем второго порядка, в зависимости от расположения корней характеристического полинома (5.10), т. е. собственных значений матрицы A.

1. ЦЕНТР – корни чисто мнимые

Чисто мнимым корням консервативной системы р _1,2 = ± i w₀ соответствует особая точка типа “центр” и фазовые траектории, образованные вложенными друг в друга эллипсами (рис. 5.6). Незатухающий колебательный процесс гармонической формы с периодом T = 2p/w₀ имеет амплитуду, определяемую начальными условиями.

Рис. 5.6 – Особая точка типа “центр”

Получим уравнение фазовых траекторий для этого случая на примере дифференциального уравнения

(5.11)

с начальными условиями

Характеристическое уравнение имеет вид

(5.13)

(5.12)

.

Корни характеристического уравнения

.

Решение дифференциального уравнения (5.11) имеет вид

(5.15)

(5.14)

где с ₁ и с ₂ – постоянные интегрирования, которые определяются заданными начальными условиями.

Вычислим постоянные интегрирования. Для этого определяем производную

Теперь используем заданные начальные условия

откуда

(5.16)

Для того, чтобы получить уравнение фазовых траекторий, нужно из уравнений (5.16) исключить время t.

(5.19)

(5.18)

(5.17)

или

Таким образом, фазовые траектории – это эллипсы с центром в начале координат и полуосями и .

Можно фазовые траектории получить другим способом. Из уравнения (5.11) получим систему уравнений

Разделим второе уравнение системы (5.19) на первое

(5.20)

Получили линейное дифференциальное уравнение с разделяющимися переменными. Решим это уравнение

(5.21)

где с – постоянная интегрирования.

Если определить постоянную с из заданных начальных условий то получим уравнение (5.18).

Вывод. Если корни характеристического уравнения являются чисто мнимыми числами , то фазовые траектории представляют собой концентрические эллипсы с центром в начале координат, а особая точка – центр.

2. Устойчивый УЗЕЛ

Если корни p ₁, p ₂ полинома (5.10) действительные отрицательные, то имеет место особая точка типа “устойчивый узел” (рис. 5.7). Прямолинейным фазовым траекториям соответствуют состояния, когда постоянные при одной из экспонент (5.9) равняются нулю. Кривые 1 и 2 соответствуют различным начальным условиям.

Рис. 5.7. Особая точка типа “устойчивый узел”

3. Неустойчивый УЗЕЛ

При положительных действительных корнях p ₁, p ₂ имеем особую точку типа “неустойчивый узел” (рис. 5.8).

Рис. 5.8. Особая точка типа “неустойчивый узел”

 

4. СЕДЛО

Если один из действительных корней отрицательный, а другой – положительный, то особая точка называется “седло” (рис. 5.9). Прямолинейные траектории ― сепаратрисы седла ― соответствуют случаю, когда один из коэффициентов в (5.10) равен нулю.

Рис. 5.9. Особая точка типа “седло”

5. Устойчивый ФОКУС

Комплексно-сопряженные корни с отрицательными действительными частями дают особую точку типа “устойчивый фокус” (рис. 5.10).

Рис. 5.10. Особая точка типа “устойчивый фокус”

6. Неустойчивый ФОКУС

Если действительные части комплексных корней положительны, то имеем “неустойчивый фокус” (рис. 5.11) и колебательные расходящиеся процессы.

Рис. 5.11. Особая точка типа “неустойчивый фокус”

Особым точкам типа “устойчивый узел” и “устойчивый фокус” соответствуют устойчивые “в малом” положения равновесия нелинейной системы. В случае особых точек “седло”, “неустойчивый узел” и “неустойчивый фокус” положения равновесия неустойчивы. В случае особой точки типа “центр” об устойчивости положения равновесия нелинейной системы нельзя судить по линеаризованным уравнениям.