
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скользящие процессы в релейных системах
Рассмотрим систему автоматического управления с нелинейным элементом типа «идеальное реле» (рис. 5.18). Структурная схема исследуемой системы показана на рис. 5.19. Построим и исследуем фазовые траектории этой системы.
Рис. 5.18. Характеристика «идеального реле»
Рис. 5.19. Структурная схема исследуемой системы с «идеальным реле» По заданной структурной схеме составим математическую модель в виде системы дифференциальных уравнений
Преобразуем математическую модель исследуемой системы с учетом свойств релейной характеристики (нечетная функция)
Движение системы происходит только за счет ненулевых начальных условий. Переменные состояния имеют следующий смысл: х 1 – выход, х 2 – скорость изменения выхода. Получим дифференциальное уравнение фазовых траекторий системы
Линия переключения реле на фазовой плоскости задается уравнением Справа от линии переключения (область I) будет выполняться неравенство Область I:
Уравнение фазовых траекторий системы в области I – это уравнение парабол, вершины которых находятся на оси x 1 фазовой плоскости, а ветви парабол направлены влево. Параболы изображены на рис. 5.20 справа от линии переключения.
Рис. 5.20. Фазовые траектории в областях I и II Направление движения изображающей точки по этим фазовым траекториям: в верхней полуплоскости – движение слева направо, в нижней полуплоскости – справа налево. Область II: «Сшивая» оба листа по линии переключения, получим фазовый портрет исследуемой системы (рис. 5.21).
Рис. 5.21. Фазовый портрет системы Пусть начальные условия таковы, что изображающая точка на фазовой плоскости занимает положение М0 в области I. Здесь
На линии скольжения происходит следующее. Как только фазовая траектория пересечет линию переключения (из области II в область I), вступит в свои права фазовая траектория из области I, которая вернет процесс на линию переключения внутри отрезка скольжения. Но тут попадаем на фазовую траекторию из области II и т. д. В результате изображающая точка будет «скользить» по линии переключения к началу координат. Это соответствует переключениям релейного элемента с большой частотой. Теоретически частота колебаний бесконечна, а их амплитуда равна нулю. Следовательно, теоретически изображающая точка скользит по линии переключения к началу координат – равновесному состоянию. Фазовой траектории М0М1М2М3 соответствует процесс во времени, показанный на рис. 5.22, где отмечены те же характерные точки.
Рис. 5.22. Траектория движения Из полученных формул и фазового портрета исследуемой системы можно сделать следующие выводы. 1. Фазовая плоскость исследуемой системы разбивается на две области, границей которых является прямая 2. На линии переключения можно выделить три характерных участка, разграниченных точками А и В – точками касания фазовых траекторий (парабол) линии переключения. За пределами отрезка АВ фазовая траектория по одну сторону линии переключения после перехода через нее является продолжением траектории по другую сторону линии переключения. Внутри отрезка АВ фазовые траектории подходят к линии переключения с двух сторон, встречаясь на нем. 3. Попав на отрезок АВ, изображающая точка уже не сможет сойти с него, но и не сможет остаться на нем. Скорость движения на АВ не определена, но специальные исследования показывают, что она конечна. Изображающая точка будет скользить по отрезку к началу координат – точке равновесия, похожей на устойчивый узел. Отрезок АВ называют отрезком скольжения.
Уравнение движения системы вдоль линии переключения Скользящий процесс происходит по экспоненциальному закону и не зависит от параметров системы, а определяется только коэффициентом обратной связи. Нелинейная система второго порядка на участке скользящего режима вырождается в линейную систему первого порядка. Найдем положение концов отрезка скользящего процесса A и B на фазовой плоскости. Очевидно, что в этих точках касательные к параболам совпадают с линией переключения. Это условие согласно уравнению
Для точки B:
4. Отрезок скользящего процесса тем больше, чем больше коэффициент усиления обратной связи. 5.3 Устойчивость нелинейных САУ Придет ли с течением времени нелинейная система к положению равновесия (или заданного движения) при начальном отклонении от этого состояния? Кажется возможным для нелинейной системы с «гладкой» нелинейностью при малых начальных отклонениях (в пределах линейной зоны) считать и в дальнейшем ее поведение близким к поведению соответствующей линейной системы и использовать известные критерии устойчивости для линеаризованной модели. Однако такой подход неверен. Процесс, начавшийся в «линейной» зоне, даже при выполнении условий устойчивости «в малом», может эту зону покинуть. При исследовании систем управления по нелинейным математическим моделям следует говорить об устойчивости конкретного движения, а не системы в целом; одни движения нелинейной системы могут быть устойчивыми, а другие ― нет. Пусть математическая модель системы представлена в форме системы дифференциальных уравнений 1-го порядка (в форме Коши)
где х ― вектор состояния; f ― вектор-функция (нелинейная). Решения системы (5.23) х* (t, х 0), при конкретных начальных условиях х 0 = х (0), следуя Ляпунову[1], называют невозмущенным движением. Выбор движения, принимаемого за невозмущенное, произволен. В частности, если начальным условиям х 0 соответствует положение равновесия, то оно и будет невозмущенным движением. Всякое другое решение дифференциальных уравнений х (t, х 0+D х 0) при иных начальных условиях х 0+D х 0 называется возмущенным. Вариация движения – это разность между возмущенным и невозмущенным движениями: D х (t) = х (t, х 0+D х 0) – х* (t, х 0). Невозмущенное движение называется устойчивым, если для любого e > 0 найдется такое d(e), что из Если в качестве невозмущенного движения принять состояние равновесия системы, то определение устойчивости можно интерпретировать так. Положение равновесия называется устойчивым, если, задав вокруг точки равновесия любую сколь угодно малую область e, можно найти такую область d(e), что помещенная в момент времени t = 0 в любую точку этой области изображающая точка в момент времени t = T войдет в область e и далее из нее не выйдет. Асимптотическая устойчивость означает, что
Устойчивость по Ляпунову ― понятие качественное (теоретическое), поскольку не оговариваются размеры области невозмущенного движения; здесь говорят об устойчивости “в малом”. Устойчивость “в большом” ― понятие количественное (практическое), когда указываются границы области притяжения. В том случае, когда область совпадает со всем пространством состояний, невозмущенное движение будет устойчивым “в целом”. Линейная система имеет единственное положение равновесия; если оно устойчиво, то устойчиво “в целом”. Разумеется, остается вопрос о том, насколько линейная модель адекватно описывает реакцию системы “в целом”. Первый метод Ляпунова Первый метод Ляпунова применяется для исследования устойчивости нелинейной системы по линеаризованным уравнениям для малых вариаций переменных. Применение метода к дифференциальным уравнениям Пусть динамическая система описывается уравнениями (5.23). Обозначим через х* вектор координат исследуемого положения равновесия, т. е. решение системы уравнений при f (х) = 0. Положим, что функции f допускают разложение в степенной ряд в точке х*. Пренебрегая малыми высшего порядка по сравнению с вариациями D х, получим вместо уравнений (5.23) линеаризованную систему
где A ― матрица первых производных нелинейных функций (матрица Якоби), вычисляемых в точке равновесия х = х*. Первый метод Ляпунова базируется на том, что об устойчивости положения равновесия нелинейной системы в “малом” можно судить по результатам анализа линеаризованной системы: · если все собственные значения матрицы А имеют отрицательные действительные части, т. е. линеаризованная система устойчива, то положение равновесия устойчиво
· если линеаризованная система неустойчива, то положение равновесия неустойчиво. Первый метод Ляпунова применяется очень часто. Однако он имеет следующие недостатки: · исследуется только устойчивость “в малом”; · метод применим только для систем, линеаризуемых в окрестности положений равновесия. Исследование устойчивости Дано дифференциальное уравнение
которое приводится к виду
Положения равновесия являются действительными решениями уравнения статики Ф(y, 0,…, 0) = 0, полученного из исходного уравнения приравниванием производных нулю. Выбирается исследуемое положение равновесия y*, и левая часть исходного уравнения раскладывается в степенной ряд при условии, что функция F аналитична в его окрестности:
Полагая, что отклонения переменной y и ее производных малы, можно пренебречь в разложении малыми высших порядков. В результате получится линейное дифференциальное уравнение
коэффициенты которого равны значениям частных производных функции F в точке равновесия. Положение равновесия исходной нелинейной системы устойчиво, если все корни характеристического уравнения Пример. Исследуем устойчивость положения равновесия осциллятора Ван дер Поля, описываемого дифференциальным уравнением второго порядка: Ф(y, y’, y”) = y” – m(1 – y 2)y’ + y = 0. Система имеет единственное положение равновесия y* = y’ = y” = 0. Линеаризованное для малых отклонений уравнение запишется так:
Характеристическое уравнение Q (p) = p 2 – m p + 1 = 0 имеет следующие корни
Положение равновесия не устойчиво, если m > 0. При значении m ³ 2 на фазовой плоскости в начале координат имеется особая точка типа “неустойчивый узел”. При значениях 0 < m < 2 там же будем иметь особую точку типа “неустойчивый фокус”. Фазовый портрет осциллятора Ван дер Поля (рис. 5.16) имеет устойчивый предельный цикл, которому соответствуют автоколебания.
Рис.. 5.16. Фазовый портрет осциллятора Ван дер Поля (0 < m < 2) В заключение отметим, что в случае нескольких положений равновесия их устойчивость исследуется поочередно. Второй метод Ляпунова Исследование устойчивости нелинейных систем является сложной проблемой. Одним из методов точного исследования устойчивости является применение теоремы Ляпунова (второй метод Ляпунова). Этот метод универсален, он не связан с линеаризацией уравнений движения и не накладывает особых ограничений на их правые части. Вместе с тем, применение второго метода Ляпунова в практике проектирования систем управления осложняется двумя обстоятельствами: · отсутствие общих рекомендаций по выбору функций Ляпунова; · достаточный характер утверждений, т. е. если условия не выполняются, то об устойчивости положения равновесия ничего сказать нельзя, можно только порекомендовать подобрать другую функцию Ляпунова. Формулировка теоремы Ляпунова. Математическая модель системы представляется в форме Коши, как система дифференциальных уравнений 1-го порядка для переходного процесса в отклонениях переменных от их значений в установившемся процессе:
Функции f 1, f 2, …, fn могут иметь произвольный вид и содержать любые нелинейности, но удовлетворяют условию f 1 = f 2 =…= fn = 0 при x 1 = x 2 =…= xn = 0, так как в установившемся состоянии все отклонения переменных и их производные равны нулю. Система устойчива, если можно подобрать такую знакоопределенную функцию Ляпунова V (x 1, x 2, …, xn), чтобы ее производная по времени W (x 1, x 2,…, xn) тоже была знакоопределенной (или знакопостоянной), но имела знак противоположный знаку V.
Функция называется знакоопределенной во всех точках области вокруг начала координат, если сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат. Функция называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области. Функция называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки. Примеры: V = x 12 + x 22 – знакоопределенная (положительная); Если производная W (x 1, x 2,…, xn) от какой-нибудь функции Ляпунова V (x 1, x 2,…, xn) окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то система неустойчива. Пример. Рассмотрим систему, описываемую уравнением Дуффинга
(нелинейные колебания пружины). Полагая у 1= у, y 2 = dy / dt, получаем нелинейную систему уравнений 1-го порядка:
Принимаем функцию V (y 1, y 2) =
При a > 0 функция W (y 1, y 2) является знакоопределенной (отрицательной). Следовательно, при a > 0, b > 0 (сильная пружина) имеем асимптотическую устойчивость: V (y 1, y 2) – знакоопределенная положительная, W (y 1, y 2) – знакоопределенная отрицательная. К сожалению, не существует общего метода построения функции Ляпунова для произвольной нелинейной системы. Однако к настоящему времени функции Ляпунова построены практически для всех наиболее важных классов нелинейных систем, встречающихся на практике. Более того, если построена функция Ляпунова, то через нее удается выразить такие показатели качества переходного процесса как перерегулирование, время переходного процесса и др.
Теорема Лурье Рассмотрим нелинейную систему с одной однозначной нелинейностью z = Ф(e). Объединив вместе все остальные (линейные) звенья системы, представим ее в следующем виде (рис. 5.17):
Рис. 5.17. Нелинейная система с обратной связью Пусть статическая характеристика Ф(е) безынерционного нелинейного элемента удовлетворяет следующим условиям: однозначна и непрерывна; Ф(0) = 0; e ∙Ф(e) > 0, т. е. график характеристики проходит через начало координат и располагается в первом и третьем квадрантах. Для этого практически важного случая А. И. Лурье[2] и В. Н. Постников предложили следующую форму функции Ляпунова (квадратичная форма от е плюс интеграл от нелинейности):
Пример. Пусть линейная часть системы имеет передаточную функцию Дифференциальное уравнение системы первого порядка в форме Коши запишется так:
Выберем следующую функцию Ляпунова:
Продифференцируем эту функцию по времени, получим:
Получили отрицательно-определенную функцию W (е), что позволяет сделать вывод об асимптотической устойчивости положения равновесия. Кроме того, замечаем, что функция Таким образом, условия устойчивости не зависят от конкретного вида нелинейности и начальных условий. Устойчивость, не зависящая от начальных условий, называется устойчивостью в целом. Устойчивость, не зависящая от конкретного вида нелинейности, называется абсолютной устойчивостью. Асимптотическую устойчивость в целом для класса нелинейностей называют абсолютной устойчивостью. В рассмотренном примере системы первого порядка положение равновесия абсолютно устойчиво. Критерий В.М. Попова Задачу исследования абсолютной устойчивости системы с одной однозначной нелинейностью можно решить с помощью частотного критерия Попова. При этом используются приемы, аналогичные частотным способам исследования устойчивости линейных систем. Если в системе автоматического регулирования имеется лишь одна однозначная нелинейность z = Ф(e), то можно объединить вместе все остальные (линейные) звенья системы и представить ее, как показано на рис. 5.17. Пусть нелинейность z = Ф(e) имеет любое очертание, не выходящее за пределы заданного угла arctg k (рис. 5.18), т. е. при любом e > 0 Ф(e) < ke, а при e > 0 Ф(e) > ke.
Рис. 5.18. Вид рассматриваемой нелинейности Пусть многочлен Q (p) (характеристический полином линейной части системы) имеет все корни с отрицательными вещественными частями. Тогда, согласно теореме В.М. Попова, для доказательства устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором для всех w ³ 0 выполняется неравенство
где G(i w ) – амплитудно-фазовая частотная характеристика линейной части системы. При наличии одного нулевого полюса G (p) требуется еще, чтобы Im G (i w) ® –¥ при w ® 0, а при двух нулевых полюсах, чтобы Re G (i w) ® –¥ при w ® 0, a Im G (i w) < 0 при малых w. Теорема справедлива также и при наличии в знаменателе передаточной функции линейной части не более двух чисто мнимых корней, но при этом требуются некоторые другие простые добавочные условия, называемые условиями предельной устойчивости.
или U *(w) = U (w), V *(w) = w V (w). Тогда (1 + i w h) G (i w) = (1 + i w h)(U + iV) = U – w hV + i (V + w hU) Þ Re {(1+ i w h) G (i w)} + 1/ k = U * –hV * + 1/ k. Условие теоремы В.М. Попова принимает вид
Очевидно, что равенство
Прямая
Рис. 5.19. Графическая интерпретация критерия Попова: а – устойчивость; б – неустойчивость Описанный частотный критерий устойчивости В.М. Попова для систем с одной однозначной нелинейностью в его графической форме может быть применен при любой сложности линейной части системы и численно заданных коэффициентах уравнений. Более того, он может быть применен в случае, когда не заданы уравнения, но известна экспериментально снятая амплитудно-фазовая частотная характеристика G (i w) линейной части. Чтобы исследовать устойчивость системы, нужно перестроить снятую амплитудно-фазовую характеристику G (i w) линейной части в модифицированную характеристику G *(i w). Очертание нелинейности может быть неизвестным. Необходимо знать лишь, в пределах какого угла она расположена. Для конкретно заданных форм нелинейности область устойчивости, вообще говоря, будет несколько шире, но данным методом это определено быть не может. Пример. Исследование устойчивости нелинейной следящей системы методом Попова. Предполагается, что ДОС имеет нелинейность типа «зона нечувствительности», (рис. 5.20, а), а усилитель – нелинейность типа «ограничение» (рис. 5.20, б).
Рис. 5.20 – Вид нелинейности системы: а, б – нелинейности и усилителя; в – нелинейность системы Предполагается, что в системе реализуется пропорционально-дифференциальный закон управления U = (1 + a p) u, где u – напряжение на выходе усилителя, U – напряжение в якорной цепи двигателя. Математическая модель объекта управления имеет вид:
Структурная схема системы изображена на рис. 5.21.
Рис. 5.21. Структурная схема системы Характеристика нелинейности:
Передаточная функция линейной части системы Условия критерия Попова для нелинейности выполняются при k = k y, т. к. нелинейность не выходит за пределы допустимого сектора: | u | = |Ф(e)| < k y| e |. Проверяем частотное условие.
Так как данное неравенство должно иметь место при любом
Величину h, удовлетворяющую этим условиям, можно подобрать при любых ky > 0, a >0: h > max { T – a – c e/ k y; – Tc e / k ya}. В этом случае условия критерия Попова выполнены и отрезок [– e 1, e 1] является поточечно устойчивым в целом, т. е. при любых начальных отклонениях установится режим, в котором e (t) = e ¥, | e ¥| £ e 1. Значит и j(t) ® j¥ = – e ¥. Иначе говоря, управляющее воздействие обеспечивает стабилизацию в окрестностях j = j* с точностью до | e 1|. За погрешность «несет ответственность» зона нечувствительности датчика. Тот же результат можно получить геометрически. Годограф
целиком лежит в третьем квадранте и легко провести прямую линию, оставляющую его справа (рис. 5.22).
Рис. 5.22. Структурная схема системы Оказывается, что сформулированный критерий Попова можно применять не только в случае однозначной стационарной характеристики Ф(e). Условие Re [(1+ ih w) G (i w)]+1/ k > 0 остается достаточным при сформулированных выше требованиях, но: · для неоднозначной характеристики с отрицательным гистерезисом при 0 £ h <¥; · для неоднозначной характеристики с положительным гистерезисом при –¥ < h <0; · для нестационарной однозначной и неоднозначной характеристики при h = 0.
Рис. 5.23. Нестационарная однозначная нелинейность Автоколебания В системе, описываемой линейным дифференциальным уравнением Q (p) y (t) = 0, при отсутствии внешних периодических воздействий может существовать колебательное решение типа y (t) = a∙sin w t (если i w корень уравнения Q (p) = 0, т. е. при Q (i w) = 0). Это решение не грубое: стоит немного изменить параметры системы, и решение уравнения превращается в затухающие или расходящиеся во времени колебания. В нелинейных системах возможна и другая ситуация: в них могут существовать грубые колебательные решения даже при отсутствии внешних периодических воздействий. Реальные процессы, соответствующие этим решениям, называют автоколебаниями, так как они определяются внутренними, собственными свойствами системы. Итак, можно разделить следующие виды колебаний: 1) свободные колебания; возникают в линейной системе при отсутствии внешних периодических воздействий; частота их определяется параметрами системы, амплитуда – начальными условиями; 2) вынужденные колебания; возникают в линейной системе (и в нелинейной) при внешних периодических воздействиях; их частота определяется частотой вынуждающей силы, амплитуда – амплитудой и частотой воздействия и параметрами системы; 3) автоколебания; возникают в нелинейной системе при отсутствии внешних периодических воздействий; их частота и амплитуда определяются параметрами системы. Если система управления организуется так, что в положении равновесия ошибка управления должна быть равна нулю, то наличие автоколебаний нежелательно. Однако если размах колебаний (максимальное отклонение от положения равновесия) лежит в пределах допустимых пределах, то автоколебательный режим приемлем. Отсюда вытекает практическая важность определения возможности возникновения и оценки параметров автоколебаний. Подчеркнем, что выполнение условий устойчивости в целом (абсолютной устойчивости) гарантирует отсутствие автоколебаний, но при проектировании СУ эти условия удовлетворяются далеко не всегда. С другой стороны, выполнение условий устойчивости «в малом» (на основе модели, линеаризованной в окрестности положения равновесия) не является достаточной гарантией отсутствия автоколебаний. Может наблюдаться режим «жесткого возбуждения»: система некоторое время работает стабильно, а затем под влиянием одиночного внешнего импульса почти внезапно самовозбуждается и переходит в режим больших колебаний.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 703; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.28.50 (0.128 с.) |




 .
. ,
,  .
. , слева - неравенство
, слева - неравенство  (область II). Получим уравнения фазовых траекторий в каждой из этих областей.
(область II). Получим уравнения фазовых траекторий в каждой из этих областей. , dx 2/ dx 1 = – c/x 2 – это дифференциальное уравнение с разделяющимися переменными:
, dx 2/ dx 1 = – c/x 2 – это дифференциальное уравнение с разделяющимися переменными: ,
,  ,
,  .
.

 , dx 2/ dx 1 = c/x 2,
, dx 2/ dx 1 = c/x 2,  – это дифференциальное уравнение фазовых траекторий исследуемой системы слева от линии переключения – уравнение парабол, вершины которых находятся на оси x 1, а ветви парабол направлены вправо. Направление движения изображающей точки: в верхней полуплоскости – справа налево, в нижней полуплоскости – слева направо.
– это дифференциальное уравнение фазовых траекторий исследуемой системы слева от линии переключения – уравнение парабол, вершины которых находятся на оси x 1, а ветви парабол направлены вправо. Направление движения изображающей точки: в верхней полуплоскости – справа налево, в нижней полуплоскости – слева направо.
 и дальнейшее движение изображающей точки происходит по фазовой траектории М0М1М2. В точке М2 происходит переключение реле
и дальнейшее движение изображающей точки происходит по фазовой траектории М0М1М2. В точке М2 происходит переключение реле  (изображающая точка достигла линии переключения). Далее изображающая точка перемещается по фазовой траектории М2М3. В точке М3 изображающая точка достигает линии переключения внутри отрезка АВ – отрезка скольжения.
(изображающая точка достигла линии переключения). Далее изображающая точка перемещается по фазовой траектории М2М3. В точке М3 изображающая точка достигает линии переключения внутри отрезка АВ – отрезка скольжения.
 – линия переключения релейного элемента системы.
– линия переключения релейного элемента системы. или
или 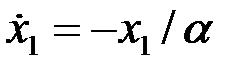 . Решение этого уравнения будет
. Решение этого уравнения будет  , где значения t = 0 (начальное значение времени движения системы по линии переключения) и x 1(0) = x 10 вычисляются в момент попадания изображающей точки на линию (отрезок) скольжения.
, где значения t = 0 (начальное значение времени движения системы по линии переключения) и x 1(0) = x 10 вычисляются в момент попадания изображающей точки на линию (отрезок) скольжения. . Тогда из уравнений траекторий получим для точки A условие в виде
. Тогда из уравнений траекторий получим для точки A условие в виде ;
;  .
.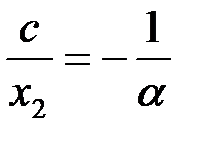 ;
; 


 для всех t > T следует:
для всех t > T следует: 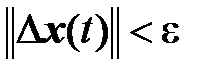 (знак
(знак  означает норму вектора).
означает норму вектора). т. е. возмущенные движения асимптотически стремятся к невозмущенному, в частности, при t ®µ приходят в состояние равновесия.
т. е. возмущенные движения асимптотически стремятся к невозмущенному, в частности, при t ®µ приходят в состояние равновесия.
 x=x*
x=x*
 a 0 y ( n ) + a 1 y ( n -1) + a 2 y ( n -2) +...+ any = 0,
a 0 y ( n ) + a 1 y ( n -1) + a 2 y ( n -2) +...+ any = 0, Ф(y, y’,…, y ( n )) = 0.
Ф(y, y’,…, y ( n )) = 0.

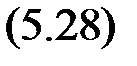









 При b > 0 функция V (y 1, y 2) является знакоопределенной (положительной). Тогда
При b > 0 функция V (y 1, y 2) является знакоопределенной (положительной). Тогда


 .
.
 .
.
 определена для всех е и при
определена для всех е и при 
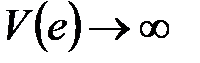 . Поэтому положение равновесия асимптотически устойчиво в целом. Наконец, обратим внимание на то, что полученный результат справедлив для целого класса нелинейных функций Ф(е), удовлетворяющих введенным выше ограничениям.
. Поэтому положение равновесия асимптотически устойчиво в целом. Наконец, обратим внимание на то, что полученный результат справедлив для целого класса нелинейных функций Ф(е), удовлетворяющих введенным выше ограничениям.


 Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики G *(i w), которая определяется следующим образом:
Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики G *(i w), которая определяется следующим образом: Re G *(i w) = Re G (i w), Im G *(i w) = w× Im G (i w)
Re G *(i w) = Re G (i w), Im G *(i w) = w× Im G (i w)

 представляет собой уравнение прямой на плоскости G *(i w):
представляет собой уравнение прямой на плоскости G *(i w):  откуда для условий выполнения теоремы Попова следует:
откуда для условий выполнения теоремы Попова следует:
 , h > 0
, h > 0 , h < 0.
, h < 0. делит всю плоскость U * V * на две полуплоскости. Условие Попова выполняется в одной из полуплоскостей, той где находится точка (0, 0). Следовательно, именно в эту полуплоскость и должна полностью попадать кривая G *(i w). Отсюда следует графическая интерпретация теоремы В.М. Попова: для устойчивости нелинейной системы достаточно подобрать на плоскости G *(i w) прямую, которая бы проходила через точку
делит всю плоскость U * V * на две полуплоскости. Условие Попова выполняется в одной из полуплоскостей, той где находится точка (0, 0). Следовательно, именно в эту полуплоскость и должна полностью попадать кривая G *(i w). Отсюда следует графическая интерпретация теоремы В.М. Попова: для устойчивости нелинейной системы достаточно подобрать на плоскости G *(i w) прямую, которая бы проходила через точку




 имеет нулевой полюс p = 0 и отрицательный полюс p = –1/ Т.
имеет нулевой полюс p = 0 и отрицательный полюс p = –1/ Т.







