Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка качества импульсной системы управленияСодержание книги
Поиск на нашем сайте
Качество импульсной системы регулирования определяют устойчивость, точность и быстродействие системы. Оценить эти характеристики можно по кривой переходного процесса, коэффициентам ошибок, частотным характеристикам. Переходный процесс позволяет судить об устойчивости, быстродействии и точности отработки постоянных входных сигналов, коэффициенты ошибок – о точности отработки полиномиальных сигналов, частотные характеристики – о точности отработки гармонических сигналов. Кривая переходного процесса описывает выходной сигнал системы, когда на ее вход при нулевых начальных условиях подается единичное входное воздействие. В импульсных системах – это единичная решетчатая функция. Кривая переходного процесса может быть снята экспериментально или определена аналитически. Пример. Построение переходного процесса в системе, где непрерывная часть является идеальным интегрирующим звеном с передаточной функцией G 0(p) = k / p, а формирующее звено – экстраполятором нулевого порядка H 0(z, p) = (z –1)/ zp (рис. 4.19).
Рис. 4.19. Импульсная система Дискретные передаточные функции разомкнутой и замкнутой системы имеют следующий вид
Изображение единичной ступенчатой функции X (z) = Z [1(t)] = z /(z –1), изображение выходной величины
Переходный процесс, т. е. значения выходной величины у (nT) в дискретные моменты времени, соответствующие n = 0, 1, 2, …, можно определить, разложив полученное выражение в ряд Лорана или воспользовавшись таблицами Z -преобразования. Напомним, что ряд Лорана, т. е. разложение Y (z) по отрицательным степеням z, можно выполнить, разделив числитель на знаменатель. Например, при kТ = 1,4 получим: 1,4z z2–0,6z-0,4 1,4/z+0,84/z2+1,064/z3+0,9744/z4+… 1,4z–0,84–0,56/z 0,84+0,56/z 0,84–0,504/z–0,336/z2 1,064/z+0,336/z2 1,064/z–0,6384/z2+0,4256/z3 0,9744/z2–0,4256/z3 Таким образом, y (0) = 0; y (1) = 1,4; y (2) = 0,84; y (3) = 1,064; y (4) = 0,9744 и т. д.

Разложим выражение
В частности, при kТ = 0,5 имеем: y (0) = 0; y (1) = 0,5; y (2) = 0,75; Значения выходной величины в дискретные моменты времени можно соединить прямыми линиями, соответствующими переходным характеристикам интегрирующего звена, которым является непрерывная часть системы.
Нетрудно заметить, что оптимальный процесс будет при kТ = 1,0, когда переходный процесс длится конечное время, равное одному периоду повторения. Вообще, в отличие от непрерывных систем, в дискретных системах переходный процесс может завершиться за конечное число тактов (в непрерывных системах время переходного процесса не может быть конечным). Это важная особенность дискретных систем. Точность импульсной системы может оцениваться по коэффициентам ошибок. Аналогично непрерывным системам, начиная с некоторого момента времени, установившуюся ошибку импульсной системы управления можно представить в виде ряда
Учитывая, что
получаем
Вычислим два первых коэффициента ошибок для замкнутой системы с передаточной функцией разомкнутой части Находим передаточную функцию по ошибке
Подстановка в это выражение z = 1 дает коэффициент с 0 = 0. Для определения коэффициента с 1 ищем первую производную
Подстановка z = 1 дает коэффициент с 1 = 1/ kT. Если на вход подобной системы поступает постоянный сигнал х [ n ] = 1, то установившаяся ошибка его отработки е уст[ n ] = 0; для линейного входа х [ n ] = n – е уст[ n ] = 1/ kT. Цифровые системы Цифровой системой называется система, в которой осуществляется дискретизация сигнала (хотя бы одного) по времени и по уровню. К цифровым системам относятся системы автоматического управления, включающие цифровые вычислительные устройства (компьютеры, программируемые контроллеры). Непосредственно в целях управления компьютеры используются для формирования программ управления и цифровой реализации алгоритмов управления или корректирующих устройств. Особенно актуально это при сложной обработке информации или выполнении операций, которые трудно реализовать при помощи аналоговых средств (нелинейные алгоритмы управления, алгоритмы самонастройки и др.). Помимо непосредственного управления объектом компьютер может выполнять операции контроля состояния элементов и устройств системы.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.51 (0.01 с.) |



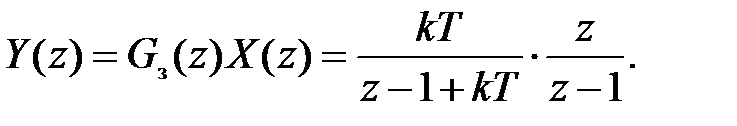
 на элементарные дроби:
на элементарные дроби:
 где коэффициенты ошибок вычисляются по формуле
где коэффициенты ошибок вычисляются по формуле