
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поведение нелинейных систем на фазовой плоскости
Исследование поведения нелинейных систем второго порядка на фазовой плоскости целесообразно начинать с определения положений равновесия – особых точек фазового портрета. Принципиальным отличием нелинейных систем от линейных является то, что положений равновесия может быть несколько или они могут отсутствовать вообще. Если в окрестности изолированных положений равновесия нелинейности достаточно гладкие, то записывают линеаризованные дифференциальные уравнения для малых отклонений от конкретных положений равновесия. По расположению собственных значений матриц или корней характеристического полинома устанавливаются типы особых точек, как это показано ранее в 5.2.2. В окрестности изолированных особых точек ― положений равновесия ― фазовые портреты нелинейных систем похожи на фазовые портреты соответствующих линеаризованных систем. По мере удаления от точек равновесия фазовые портреты нелинейных систем могут иметь качественные отличия. Для построения фазовых траекторий используют графические, аналитические и численные методы. Наиболее простым графическим методом решения дифференциальных уравнений (5.4), (5.8) является метод изоклин. Изоклина ― кривая равного наклона касательных к фазовым траекториям. Ее уравнение получается приравниванием правых частей (5.3) или (5.7) заданному наклону c:
Параметр c семейства изоклин равен тангенсу угла наклона касательных к фазовым траекториям. Совокупность наклонов ci выбирается так, чтобы изменение угла между двумя соседними изоклинами было примерно одинаковым. Пример. Решение уравнения Приводим уравнение к виду:
Строим изоклины
Рис. 5.12. Изоклины и интегральные кривые Для построения изоклины В этой точке с = –1/(–0,1) = 10, α = arctg10 = 84°. Строим короткий отрезок под углом α = arctg c = –84°; попадаем в точку (0,95; –0,2).
В этой точке с = –0,95/–0,2 = 4,75, α = arctg4,75 = 78°. Продолжаем процесс дальше. Попадаем в точку (0; –1). В этой точке с = –0/(–1) = 0, α = arctg0 = 0°. Строим короткий отрезок под углом α = arctg 0 = 0° и т. д. После этого соединяем все полученные точки гладкой кривой и получаем частное решение – интегральную кривую. Выбирая различные начальные условия, получим семейство интегральных кривых, которое и дает решение дифференциального уравнения. В некоторых случаях возможно аналитическое решение дифференциальных уравнений для фазовых траекторий (5.3), (5.7).
Рассмотрим уравнение математического маятника
Маятник имеет счетное множество положений равновесия: j= np; n = 0, ±1, ±2,.... Линеаризованное уравнение для малых отклонений от нижних положений равновесия (четных n) имеет вид
Рис. 5.12. Фазовый портрет маятника Видим, что при изменении параметров системы качественные свойства особой точки (тип особой точки) изменяются. Изменение типа особой точки системы при изменении значений ее параметров называется бифуркацией. Сепаратрисы, образованные слиянием искривленных “усов” седел, оказываются границами областей с колебательным движением; незамкнутые траектории вне этих областей изображают неравномерные вращательные движения маятника вокруг точки подвеса. Для получения аналитических выражений для фазовых траекторий маятника запишем его дифференциальное уравнение в форме Коши:
Деление второго уравнения на первое дает дифференциальное уравнение первого порядка:
решая которое при различных начальных условиях (j10, j20), получаем выражения для интегральных кривых на плоскости (j1, j2).
Фазовый портрет маятника изображен на рис. 5.12. В случае линейных систем автоматического управления характер (тип) особой точки определяет движение системы при любых отклонениях от состояния равновесия. Для нелинейных систем характер особой точки определяет поведение фазовых траекторий лишь в некоторой малой окрестности особой точки. При рассмотрении поведения фазовых траекторий нелинейных систем на всей фазовой плоскости весьма важную роль играют особые траектории. Особые траектории Различают три основных типа особых траекторий: 1. Особые точки (состояние равновесия). Типы особых точек рассмотрены выше. 2. Изолированные замкнутые траектории. Изолированность замкнутой траектории означает, что в достаточно малой ее окрестности нет других замкнутых траекторий. Изолированные замкнутые траектории называются предельными циклами. Предельным циклам на фазовой плоскости соответствуют периодические движения системы. Предельный цикл называется устойчивым, если существует такая окрестность этого цикла, что все фазовые траектории, начинающиеся в этой окрестности, асимптотически при Устойчивым предельным циклам в системе автоматического управления соответствуют автоколебания. Характерная черта автоколебаний – локальная независимость их параметров от начальных условий.
а б Рис. 5.13. Фазовый портрет маятника: а – устойчивый предельный цикл; б – неустойчивый Если в любой, сколь угодно малой окрестности предельного цикла существует хотя бы одна фазовая траектория, не приближающаяся к предельному циклу при 3. Сепаратрисы разделяют фазовую плоскость на области с фазовыми траекториями различных типов. В окрестности особой точки типа «седло» сепаратрисы являются асимптотами. Обычно на фазовой плоскости особых траекторий (т. е. точек равновесия, предельных циклов и сепаратрис) имеется конечное число. Определив их, находят все качественные особенности фазовых траекторий на плоскости, а по ним - все виды и особенности процессов в нелинейных системах. Пример. Фазовый портрет релейной системы (рис. 5.14).
Рис. 5.14. Релейная система В случае нелинейного элемента типа “реле с зоной нечувствительности” можно сразу найти положения равновесия: z = 0 как вход интегратора k/p в равновесном состоянии: ½ x ½ £ d; ½ y ½£ d. Имеет место отрезок равновесия. Для построения фазового портрета запишем дифференциальные уравнения системы в форме Коши:
Если учесть, что функция F (x 1) кусочно-линейная, то переменные можно разделить и проинтегрировать уравнение на различных интервалах x 1
где С – постоянная, определяемая начальными условиями. Для различных интервалов изменения x 1получим следующие уравнения для фазовых траекторий:
На рис. 5.15 показан фазовый портрет релейной системы “с зоной нечувствительности”. Линиям x 1= ±d(так называемым линиям переключения реле)соответствуют границы трех “листов” (частей) фазовой плоскости. Движения системы завершаются на отрезке равновесия.
Если модель системы содержит НЭ с кусочно-постоянной (или кусочно-линейной) характеристикой, то процесс может быть разбит на ряд интервалов так, что в пределах каждого интервала движение описывается линейными дифференциальными уравнениями.
Рис. 5.15. Фазовый портрет системы с НЭ типа На фазовой плоскости каждому линейному участку такой характеристики нелинейного элемента соответствует отдельная область или лист, в пределах которого правые части дифференциальных уравнений линейны, а фазовые траектории составлены из дуг траекторий линейных систем. Излому или разрыву таких статических характеристик нелинейных элементов соответствует граница листа фазовой плоскости (линия переключения). Если нелинейный элемент имеет характеристику типа реле с гистерезисом, то система не может иметь положений равновесия, так как всегда z ¹ 0. Фазовая плоскость состоит из двух листов. Границами листов являются в верхней полуплоскости прямая x 1= d, а в нижней – прямая x 1= –d. Фазовый портрет показан на рис. 5.16. Выделяется устойчивый предельный цикл; система функционирует в автоколебательном режиме. Анализ показывает, что фазовые траектории, начинаясь из произвольной точки фазовой плоскости, сходятся к некоторой замкнутой кривой, т. е. образуют сходящиеся спирали. На фазовой плоскости есть предельный цикл, следовательно, в системе есть автоколебания.
Рис. 5.16. Фазовый портрет системы с НЭ типа “реле с гистерезисом” Если начальные условия таковы, что изображающая точка находится внутри предельного цикла, то процесс в системе будет иметь вид, представленный на рис. 5.17, а. Если начальные условия на фазовой плоскости лежат вне предельного цикла, то процесс будет иметь вид, представленный на рис. 5.17, б. Автоколебания происходят около петли гистерезиса с амплитудой, несколько превышающей величину b.
а б Рис. 5.17. Автоколебания
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 776; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.152.99 (0.02 с.) |
 графическим методом.
графическим методом.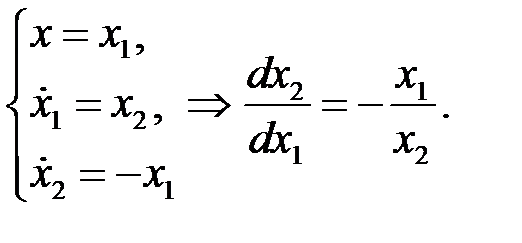
 для различных начальных условий. В каждой точке изоклины строим короткий отрезок под углом α = arctg c, получая следующую точку. По полученным отрезкам (направлениям) строим интегральные кривые (рис. 5.12).
для различных начальных условий. В каждой точке изоклины строим короткий отрезок под углом α = arctg c, получая следующую точку. По полученным отрезкам (направлениям) строим интегральные кривые (рис. 5.12).
 берем на фазовой плоскости точку с конкретными начальными условиями, например,
берем на фазовой плоскости точку с конкретными начальными условиями, например, Пример. Фазовый портрет математического маятника.
Пример. Фазовый портрет математического маятника.
 , а для отклонений от верхних положений равновесия (нечетных n):
, а для отклонений от верхних положений равновесия (нечетных n):  .
. Характеристический полином дифференциального уравнения для нижних положений равновесия Q (р) = р 2 + k 2 = 0 имеет пару мнимых корней р 1,2 = ± i×k. Следовательно, этим положениям равновесия отвечает особая точка типа “центр”. Характеристический полином для верхних положений равновесия Q (р) = р 2 – k 2 = 0 имеет действительные корни разных знаков р 1 = + k, р 2 = – k; этим положениям равновесия отвечает особая точка типа “седло” (рис. 5.12).
Характеристический полином дифференциального уравнения для нижних положений равновесия Q (р) = р 2 + k 2 = 0 имеет пару мнимых корней р 1,2 = ± i×k. Следовательно, этим положениям равновесия отвечает особая точка типа “центр”. Характеристический полином для верхних положений равновесия Q (р) = р 2 – k 2 = 0 имеет действительные корни разных знаков р 1 = + k, р 2 = – k; этим положениям равновесия отвечает особая точка типа “седло” (рис. 5.12).



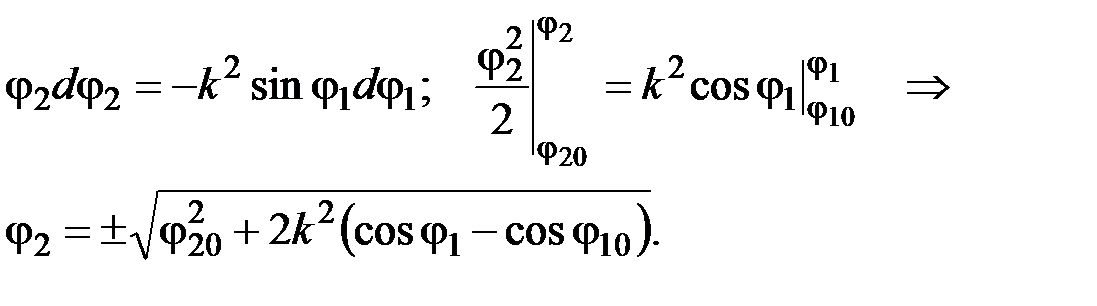
 приближаются к предельному циклу (рис. 5.13, а).
приближаются к предельному циклу (рис. 5.13, а).












