
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная система в пространстве состояний
Метод пространства состояний был разработан в 60-70 годах XX в. американскими и советскими учеными. Сущность метода может быть резюмирована в следующих положениях: - не используется преобразование Лапласа, анализ и синтез осуществляется непосредственно с использованием математического аппарата линейных дифференциальных уравнений; - объект управления представляется в виде
где u – управляющее воздействие, x – вектор пространства состояний, - постулируется, что для линейного объекта в пространстве состояний линейная пропорциональная обратная связь стабилизирует его динамику, т. е. асимптотически обращает в ноль производные вектора состояния, - для решения задач синтеза и анализа систем используются численные и оптимизационные алгоритмы, реализованные программно, в т. ч. и в системе MATLAB. Пример. Описание «грузика на пружинке в пространстве состояний
Рис. 2.9. Модель «грузика на пружинке» Уравнение движения грузика на пружинке имеет вид
Выбор переменных состояния не является однозначным, они могут быть определены по-разному, например, в нормальной, канонической или в других формах. В общем случае описание линейной САУ дается в форме динейного дифференциального уравнения n -го порядка, связывающего выход y с сигналом управления u и возмущением f. Это уравнение всегда можно представить в виде системы дифференциальных уравнений 1-го порядка:
где введены n независимых переменных х 1, х 2, …, хn, называемых переменными состояния. Эти уравнения, как и уравнение n -го порядка, полностью характеризуют состояния объекта в любой момент времени (и являются уравнениями состояния). Управляемая величина у однозначно определяется через выбранные переменные состояния х 1, х 2, …, хn выражением вида
Обычно уравнения состояния записывают в векторно-матричной форме
где A – матрица размером n ´ n, b, m, c – матрицы-столбцы. Матрицу-столбец х называют вектором состояния, хотя в общем случае х не является вектором, так как его компоненты x 1, x 2, …, xn могут иметь разный физический смысл (и неодинаковые размерности).
В выборе переменных состояния имеется определенная свобода. Важно только, чтобы они были независимыми. От того, как выбраны переменные, зависит форма уравнений состояния, т. е. вид входящих в них матриц. При нормальной форме уравнений состояния в качестве переменных состояния выбираются сама управляемая величина y и
Эту форму можно использовать лишь при отсутствии в правой части дифференциального уравнения производных от u и f, т. е. когда оно имеет вид
В этом случае
При нормальной форме записи y = x 1. Поэтому с Т = [1 0 … 0]. Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл, а некоторые из них (например, х 1, х 2 и х 3) могут быть непосредственно измерены датчиками различных типов. Для получения уравнений состояния в канонической форме уравнение объекта представляется в виде
Если корни p 1, p 2, …, pn полинома Q (p) действительные некратные, то правая часть этого уравнения может быть представлена в виде суммы элементарных дробей:
где α i и β i – коэффициенты разложения. В качестве переменных состояния выбирают слагаемые этой суммы:
Отсюда (p – pi) xi = α iu + β if, i = 1, 2, …, n или
При этом
Матрицы в уравнениях состояния принимают вид
Большое достоинство канонической формы – диагональность матрицы А, что существенно упрощает исследование. Основной недостаток состоит в том, что переменные состояния не имеют ясного физического смысла и не могут быть непосредственно измерены. Кроме нормальной и канонической формы существуют и другие способы выбора переменных состояния. 2.2 Элементарные звенья Как уже говорилось выше, для представления отдельных элементов (звеньев) в ТАУ используется стандартная форма (рис. 2.11).
Рис. 2.11. Стандартная форма представления звена x (t), y (t) – входной и выходной сигналы, G (p) – передаточная функция. Существует некоторый набор простых, стандартных моделей, с помощью которого можно описать свойства различных сложных систем. Компоненты этого набора называются элементарными звеньями.
2.2.1 Безынерционное звено Основные характеристики звена: · передаточная функция G (p) = k, k – коэффициент усиления звена; · уравнение звена y (t) = G (D) x (t) Þ y (t) = kx (t); · переходная функция (реакция на единичный скачок) x (t) = 1[ t ] Þ h (t) = k× 1[ t ] (рис. 2.12, а); · весовая функция (реакция на импульсное воздействие) x (t) = d(t) Þ g (t) = k× d(t) (рис. 2.12, б); · амплитудно-частотная характеристика A (w) = k; · логарифмическая амплитудно-частотная характеристика · логарифмическая фазо-частотная характеристика j(w) = 0.
а б в Рис. 2.12. Характеристики безынерционного звена: Итак, для статического звена характерно то, что ПФ является константой, связь между входом и выходом – пропорциональная зависимость. Звено характеризуется единственным параметром – коэффициентом усиления k. Примеры. а) редуктор j1(t) j2(t) M 1(t) M 2(t) 1/ i i Модели разные в зависимости от того, что исследуется (и, соответственно, выступает в роли входа и выхода). Исследуем кинематику: j2(t) = 1/ i ×j1(t) (k = 1/ i), силовые характеристики: б) электрический усилитель u 1(t) u 2(t) k u 2(t) = k u 1(t); G (p) = k. в) делитель напряжения
R 1 u вх R 2 u вых Замечание. Элементарные звенья – это простейшие звенья, идеализированные модели реальных элементов. Их область применимости ограничена по полосе частот и амплитуде входного воздействия. Поясним сказанное на примере электрической цепочки. Если u вх невелико, то справедлив закон Ома для участка цепи, т. е. линейная зависимость выходного сигнала (тока i через резистор) от входного (напряжения u вх): i = u вх/ R. При больших значениях u вх резистор сгорит и линейная зависимость нарушится. Следовательно, указанная зависимость (и соответствующая модель) справедлива лишь в некотором диапазоне входных воздействий. С другой стороны, при работе в области высоких частот (МГц) на процессы начнут влиять паразитные параметры (индуктивное сопротивление резистора). И в этом случае модель идеального усилителя непригодна для описания работы электрической цепочки. Аналогичная картина имеет место для усилителей напряжения (вид АЧХ на аппаратуре). В механике – при высоких скоростях происходит деформация зубьев, не проходит на выход высокочастотная составляющая. 2.2.2 Идеальный интегратор Основные характеристики: · передаточная функция G (p) = k/p; k – коэффициент усиления звена; · уравнение звена y (t) = G (D) x (t) Þ Dy (t) = kx (t) (выходной сигнал является интегралом от входа), y ’ = kx (t), y = k∙ ò x (t) dt; · переходная функция h (t) = kt (рис. 2.13, а); · весовая функция g (t) = k (рис. 2.13, б); · АЧХ A(w) = k/w; · ЛАЧХ L (w) = 20 lg k – 20 lg w (рис. 2.13, в); ФЧХ j(w) = – p/2.
а б в Рис. 2.13. Характеристики идеального интегратора: а – переходная функция, б – весовая функция, в – логарифмические частотные характеристики Описание идеального интегратора в пространстве состояний:
Пример. Гидродвигатель (рис. 2.14) В гидроприводах в качестве энергоносителя выступает сжатая гидравлическая жидкость, потенциальная энергия которой преобразуется в механическую работу путем воздействия на рабочий орган гидродвигателя. По сравнению с электроприводом гидропривод имеет следующие преимущества:
- возможность создания больших усилий при малых собственных габаритах; - возможность создания «прямого», без механизмов преобразования, привода линейных перемещений; - гидродвигатели, в отличие от электродвигателей, не выходят из строя при перегрузке, они просто останавливаются; - гидродвигатели легко регулируются по усилию и скорости; обеспечивают плавное движение; - гидродвигатели надежно работают в условиях повышенной влажности и загрязненности окружающей среды, не требуют дополнительного охлаждения; - в гидроприводе не используются высокие, опасные для человека, напряжения электрического тока.
Рис. 2.14. К математической модели гидродвигателя Силовой гидропривод предназначен для усиления мощности сигналов. Вход – перемещение x золотника, выход – перемещение y силового цилиндра. Модель включает следующие соотношения: · выражение для объемного расхода жидкости Q = S (x)m v, где S (x) – площадь открытого окна золотника; v – скорость движения жидкости; m – коэффициент, учитывающий потери. · выражение для скоростного напора D p = r v 2/2, где D p – перепад давлений; r – плотность жидкости. · условие неразрывности потока (“сколько втекает, столько вытекает”): Q 1 = Q 2 = Fy ’, где F – площадь поршня силового цилиндра. · уравнение движения поршня my ’’= (P 1 – P 2) F, где m – масса поршня. Не учитывая инерционных свойств, имеем (при m = 0):
Будем считать, что при x = 0 окно золотника полностью закрыто. Тогда S (x) @ b D x, где b – ширина окна, D x – смещение золотника относительно указанного положения отсчета. В результате
Итак, скорость движения поршня рабочего цилиндра пропорциональна перемещению золотника. Другие примеры интегрирующих звеньев – электродвигатель, резервуар, заполняемый водой. 2.2.3 Идеальное дифференцирующее звено Основные характеристики: · передаточная функция G (p) = k×p; k – коэффициент усиления звена; · уравнение звена y (t) = G (D) x (t) Þ y (t) = k×dx (t)/ dt – (выход пропорционален скорости изменения входа); · переходная функция h (t) = k ×d[ t ]; · весовая функция g (t) = k ×d'(t). L +20 дБ/дек · амплитудно-частотная A (w) = kw · ЛАЧХ L (w) = 20 lgk w; j w · ФЧХ j(w) = π/2. π/2 w Пример. Тахогенератор - электрическая машина, вал которой соединяют непосредственно или через редуктор с валом нагрузки, когда хотят определить скорость его вращения. На клеммах ТГ возникает напряжение пропорциональное скорости вращения вала:
2.2.4 Инерционное (апериодическое) звено Характеристики апериодического звена: · передаточная функция G (p) = 1/(Tp +1), T – постоянная времени; · уравнение звена y (t) = G (D) x (t) Þ · переходная функция h (t) = 1 – e -t/T (рис. 2.15, а); · весовая функция g (t) = 1/ T ×e -t/T (рис. 2.15, б); · амплитудно-частотная A (w) = · · асимптотическая ЛАЧХ ·

в Рис. 2.15. Характеристики апериодического звена: Пример. Гидроусилитель (рис. 2.16)
Рис. 2.16. К математической модели гидроусилителя Математическая модель:
Пример. Электропривод с нагрузкой
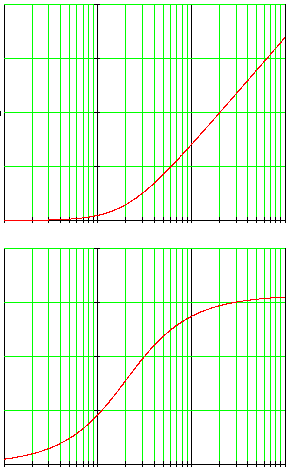
2.2.5 Колебательное звено Характеристики колебательного звена: · передаточная функция G (p) = 1/(T 2 p 2+2 T x p +1), T – постоянная времени, · уравнение звена y (t) = G (D) x (t) Þ · переходная функция · весовая функция g (t) = · амплитудно-частотная A (w) = ЛАЧХ L (w) = · асимптотическая ЛАЧХ · ФЧХ j(w) = – arctg [2 Tx w/(1– T 2w2)].

в Рис. 2.17. Характеристики колебательного звена: а – переходная функция, Примеры (груз на пружине, колебательный контур). 2.2.6 Другие элементарные звенья – Консервативное звено G (p) = 1/(T 2 p 2+1); – Дифференцирующее (форсирующее) звено 1-го порядка – Дифференцирующее звено 2 - го порядка G (p) = T 2 p 2+2 T x p +1. Отметим, что логарифмические частотные характеристики дифференцирующих звеньев 1-го и 2-го порядков получаются зеркальным отображением относительно оси абсцисс соответствующих им инверсных звеньев: апериодического и колебательного (рис. 2.18, а).
а б Рис. 2.18. Логарифмические частотные характеристики дифференцирующего (форсирующего) звена: Реальные элементы (системы) представляют собой соединение элементарных звеньев. В частности, двигатель–редуктор (усилитель, идеальный интегратор, апериодическое звено). Другие примеры: апериодическое звено 2-го порядка G (p) = k /(T 1 p +1)(T 2 p +1), интегрирующее звено с замедлением G (p) = k/p (Tp +1), изодромное звено G (p) = k (Tp +1)/ p, дифференцирующее звено с замедлением G (p) = kp /(Tp +1). 2.2.7 Неустойчивые (неминимально-фазовые) звенья Рассмотренные звенья позиционного типа (безынерционное, апериодическое, колебательное) относятся к устойчивым звеньям, или к звеньям с самовыравниванием. Выход таких звеньев приходит к новому установившемуся значению при ограниченном изменении входа (или возмущающего воздействия). Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например, звенья интегрирующего типа (линейный рост выходного сигнала во времени).
У некоторых звеньев этот процесс выражен еще заметнее, чем у интегрирующего ¾ выходной сигнал возрастает во времени по экспоненте. Такие звенья имеют в характеристическом уравнении положительные вещественные корни или комплексные корни с положительной вещественной частью. Они относятся к категории неустойчивых или неминимально-фазовых звеньев. У неминимально-фазовых звеньев имеются отрицательные коэффициенты в знаменателе передаточной функции. Рассмотрим в качестве примера подобного звена неустойчивое апериодическое звено, описываемое дифференциальным уравнением Tdy/dt – y = kx. Ему соответствует передаточная функция Частотные характеристики неминимально-фазовых звеньев Амплитудные характеристики неминимально-фазовых звеньев совпадают с амплитудными характеристиками соответствующих устойчивых звеньев, а фазовые характеристики отличаются (меньше по величине) фазовых характеристик соответствующих минимально-фазовых. Сравним для примера логарифмические частотные характеристики апериодического звена (рис. 2.19, а) и его неминимально-фазового аналога (рис. 2.19, б).
а б Рис. 2.19. Логарифмические частотные характеристики устойчивого (а) и неустойчивого (б) апериодического звена Для звена с ПФ G (p) = 1/(Tp + 1) A (w) = 1/Ö1+ T 2w2, L (w) = 20 lg (1/Ö1+ T 2w2), j(w) = – arctg (w T). Для звена с ПФ G (p) = 1/(Tp - 1) A (w) = 1/Ö1+ T 2w2, L (w) = 20 lg (1/Ö1+ T 2w2), j(w) = –p + arctg (w T). Тест (на 10 мин) 1. На вход интегрирующего звена подается сигнал x (t) = t +1. Каким будет сигнал на выходе звена? 2. На вход звена с передаточной функцией G (p) = p +1 подан сигнал x (t) = t. Нарисуйте график изменения выхода y (t). 3. Опишите в пространстве состояний звено с передаточной функцией Gy/u (p) = k /(Tp +1). 4. По дифференциальному уравнению звена 5. Определите амплитудно-частотную характеристику звена, заданного дифференциальным уравнением
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1056; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.89 (0.079 с.) |

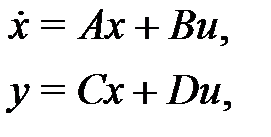
 ; другими словами, стабилизирующая обратная связь ищется в виде
; другими словами, стабилизирующая обратная связь ищется в виде  ,
, – матрица постоянных коэффициентов;
– матрица постоянных коэффициентов;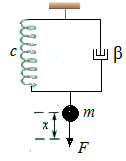
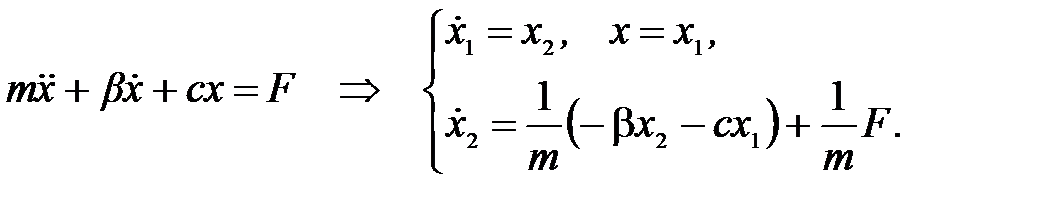
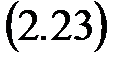
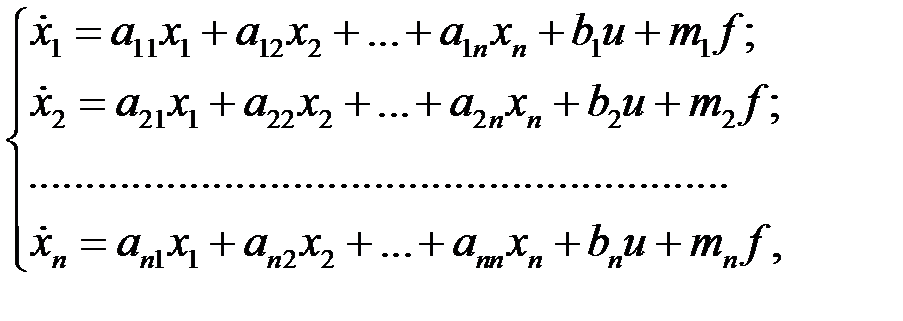
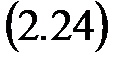 y = с 1 x 1 + с 2 x 2 + … + сnxn.
y = с 1 x 1 + с 2 x 2 + … + сnxn.


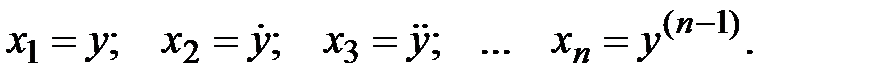
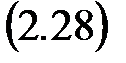
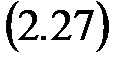
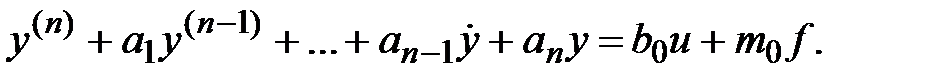

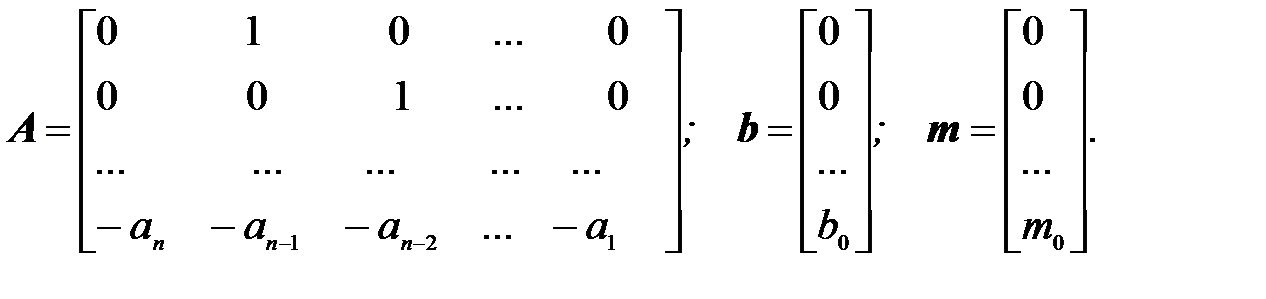
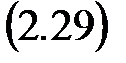
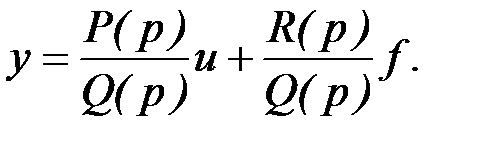


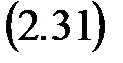


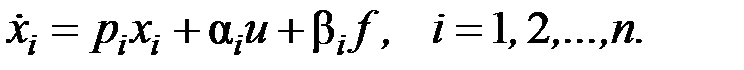
 y = x 1 + x 2 + … + xn.
y = x 1 + x 2 + … + xn.
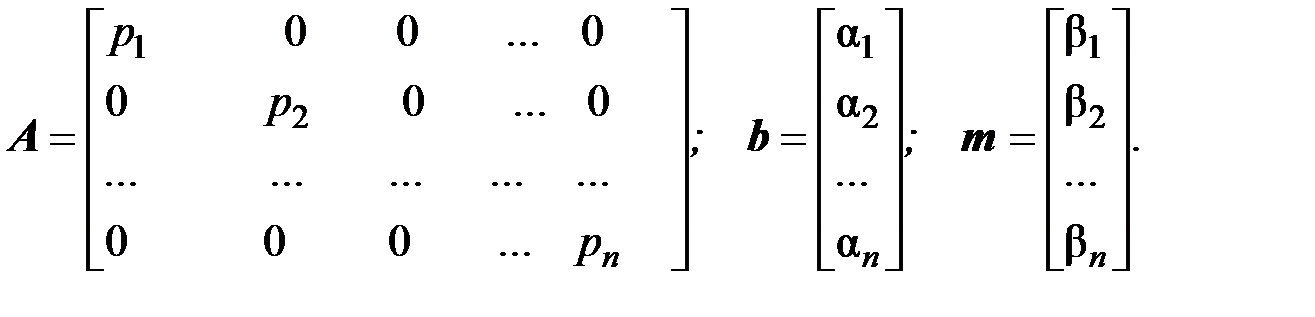
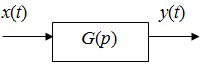

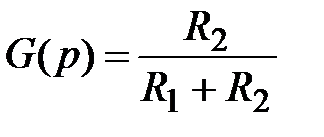

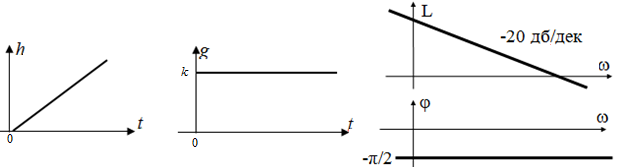



 .
.

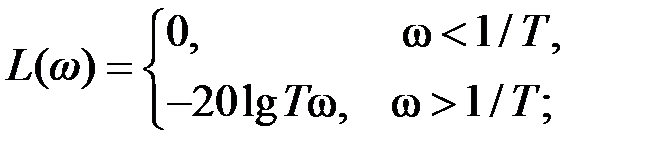 ЛЧХ L (w) = –10 lg (1+ T 2w2) (рис. 2.15, в);
ЛЧХ L (w) = –10 lg (1+ T 2w2) (рис. 2.15, в);

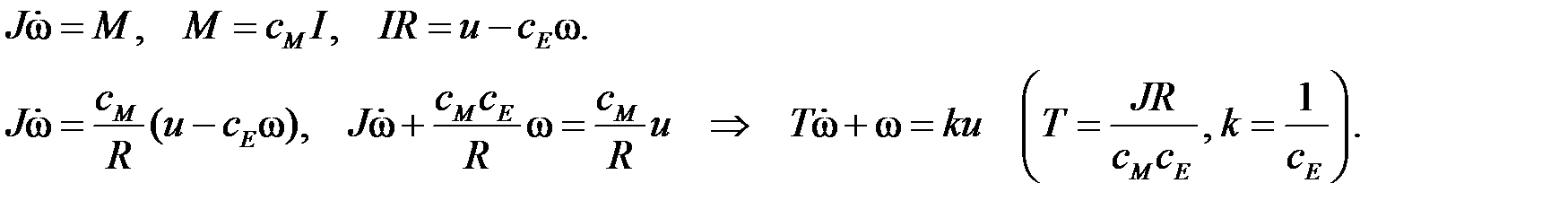

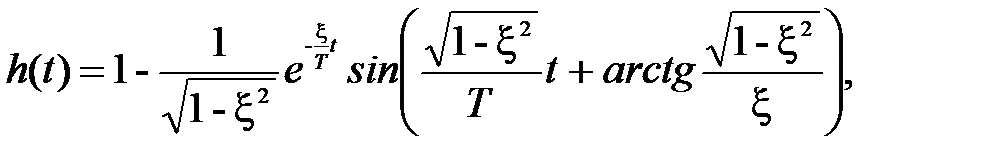 (рис. 2.17, а);
(рис. 2.17, а); (рис. 2.17, б);
(рис. 2.17, б);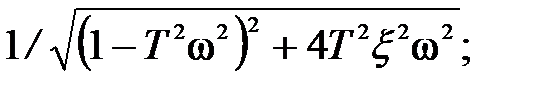
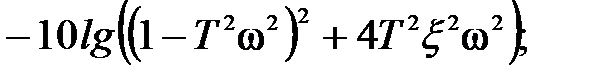 (рис. 2.17, в);
(рис. 2.17, в);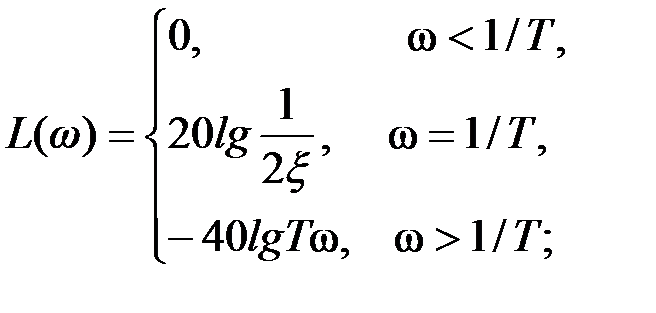


 определите передаточную функцию Gy/х (p).
определите передаточную функцию Gy/х (p).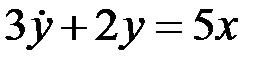 .
.


