
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Управляемость и наблюдаемость объектов
Управляемость и наблюдаемость являются такими же важными свойствами объектов, как и их устойчивость. Термин управляемость означает возможность перевода объекта из любого начального состояния (режима работы) X (t 0) = X 0 в любое конечное состояние X (t к) = Xк за конечное время Термин наблюдаемость означает возможность определения начального состояния объекта X 0 по результатам наблюдений за его выходом Y (t) на конечном интервале Итак, управляемость объекта означает возможность достижения его любого состояния, а наблюдаемость – возможность определения состояния в любой момент. Для оценки управляемости и наблюдаемости используются уравнения состояния и уравнение выхода объекта в их векторно-матричной форме
где X – вектор-столбец переменных состояния[1 ´n ]; Y – вектор-столбец выходных переменных [1 ´q ], q £ n; U – вектор-столбец управлений [1 ´ m ], m £ n; Система описывается n переменными состояния, q выходными переменными и m управляющими переменными. Управляемость объекта Если объект полностью управляем, то всегда найдется такое допустимое управление, которое за конечное время обеспечит перевод объекта из любого начального состояния в любое заданное конечное состояние. Оценка управляемости осуществляется на основе критерия Р. Калмана, согласно которому для полной управляемости объекта необходимо и достаточно, чтобы выполнялось условие
Ранг составной матрицы должен равняться порядку системы. Составная матрица имеет n строк и n´m столбцов: первые m столбцов – это столбцы матрицы B, следующие m столбцов - столбцы матрицы AB, затем - матрицы A 2 B и т. д.; последние m столбцов, с (n´m-m +1)-го по (n´m)-ый – столбцы матрицы A n -1 B.
Ранг матрицы определяется наивысшим из порядков миноров этой матрицы, отличных от нуля. Так как в рассматриваемой матрице n строк, то проверке подлежат все миноры n –го порядка, которые из нее можно составить (взяв любые n столбцов). Если хотя бы один из таких определителей не будет равен нулю, то критерий Калмана (2.67) выполняется и, следовательно, объект полностью управляем. В частном случае, когда m = 1 (B = b – столбец размерностью n´ 1), проверка сводится к вычислению единственного определителя Пример. Исследуем управляемость объекта в системе двигатель – редуктор–нагрузка. Математическая модель этой системы была получена ранее:
Запишем уравнения динамики в форме Коши:
Входом системы является напряжение Запишем уравнения модели в матричном и стандартном видах
где Найдем определитель блочной матрицы
Блочная матрица
Ее определитель не равен нулю и, значит, ранг этой матрицы равен 2. Критерий Калмана выполняется, рассматриваемая система является полностью управляемой. За счет выбора управляющего сигнала Отметим, что в некоторых случаях проверка критерия Калмана упрощается: в случае, когда матрица А объекта имеет каноническую диагональную форму (2.68) или каноническую жорданову форму (2.69), а также при известном ранге матрицы B. Если матрица А объекта имеетканоническую диагональную форму (2.68), то согласно критерию Е. Гильберта для полной управляемости такого объекта необходимо и достаточно, чтобы матрица В не содержала нулевых строк.
где l1 ¹ l2 ¹ … ¹ ln. Если матрица A объекта имеет каноническую жорданову форму (2.69), то для полной управляемости такого объекта необходимо и достаточно, чтобы последняя строка матрицы B была ненулевой.
Наконец, если модель объекта может быть представлена в нормальной форме, когда в качестве переменных состояния выбираются сама управляемая величина y и n –1 ее производных, то такой объект полностью управляем.
В этом случае
На практике для исследования управляемости ранги обычно не считают, а используют компьютерные программы. В частности, в MATLAB функция ctrb собирает аргумент B, AB, A 2 B, …, а функция rank считает определитель: rank (ctrb (A,B)). Управляемость по выходу Если критерий полной управляемости объекта позволяет судить о достижении его любого состояния, т. е. любого вектора Х (переменных состояния), то управляемость по выходу означает возможность получения любого вектора Y (выхода).
где q – число выходных переменных объекта (или число строк матрицы C). Для примера с двигателем имеем: y = j Þ q = 1.
Определитель не равен нулю, ранг равен единице. Критерий полной управляемости по выходу выполнен. Следовательно, за счет выбора управляющего сигнала Наблюдаемость объекта Как уже было сказано выше, у полностью наблюдаемого объекта можно определить начальное состояние X 0 по результатам наблюдений за его выходом Y (t) на конечном интервале
Рис. 2.59. Графики наблюдаемых переменных состояния На рис. 2.59 показаны графики двух наблюдаемых переменных состояния x 1(t), x 3(t), которые являются компонентами вектора выхода Y (t) трехмерного объекта (y 1 = x 1, y 2 = x 3). Если объект полностью наблюдаемый, то по известным начальным значениям y 10 = x 10, y 20 = x 30 и последующим значениям x 1 i, x 3 i при ti ≤ t к можно вычислить начальное значение x 20 и другие последующие значения переменной x 2(t). Согласно критерию Р. Калмана для полной наблюдаемости объекта необходимо и достаточно, чтобы выполнялось условие
где Т – символ операции транспонирования матриц. Так же, как и в критерии управляемости, при исследовании наблюдаемости использование критерия упрощается при известном ранге матрицы С, канонической диагональной форме матрицы A или ее канонической жордановой форме. Для исследования наблюдаемости в MATLAB используют функцию obsr. Синтаксис следующий: rank (obsr (С,A)). Пример. Проверяем критерий управляемости Калмана для системы двигатель–редуктор–нагрузка:
Критерий выполняется, система полностью наблюдаема. Имеется существенная разница между наблюдаемостью по Калману и обычной практической наблюдаемостью (измеряемостью) объекта. С практической точки зрения наблюдаемыми являются лишь те переменные состояния, которые можно непосредственно измерить с помощью существующих измерительных устройств. Наблюдаемыми же по Калману являются не только непосредственно измеряемые переменные, но и те переменные, которые могут быть вычислены как некоторые функции непосредственно измеряемых переменных. Очевидно, что полная наблюдаемость по Калману является лишь необходимым, но недостаточным условием практической наблюдаемости. С другой стороны, полная практическая наблюдаемость, означающая возможность непосредственного измерения всех переменных состояния объекта, является достаточным, но отнюдь не обязательным условием полной наблюдаемости по Калману. Действительно, если все переменные состояния доступны непосредственному измерению, то матрица наблюдаемости имеет диагональный вид: С = C T = diag (c 11, c 22, …, cnn), где cii – коэффициенты передачи измерительных устройств. При этом
2.6.3 Оценка управляемости и наблюдаемости объектов Всякий сложный объект состоит из отдельных, связанных между собой блоков. Для каждого блока на основании его передаточной функции можно получить уравнения состояния и по ним, применяя указанные выше критерии, оценить управляемость и наблюдаемость. Для оценки управляемости и наблюдаемости всего объекта можно использовать следующие теоремы. Теорема 1. Для полной управляемости и полной наблюдаемости объекта, состоящего из параллельно соединенных блоков, необходимо и достаточно полной управляемости и наблюдаемости каждого отдельного блока.
Теорема 2. Для полной управляемости и наблюдаемости объекта, состоящего из последовательно соединенных блоков, необходимо (но недостаточно) полной управляемости и наблюдаемости каждого блока.
Теорема 3. Для полной управляемости и наблюдаемости объекта с обратной связью необходимо и достаточно полной управляемости и наблюдаемости последовательного соединения блоков прямого канала и цепи обратной связи.
Можно дать и другую формулировку теоремы 3: для полной управляемости и наблюдаемости замкнутой САУ необходимо и достаточно полной управляемости и наблюдаемости соответствующей разомкнутой САУ. Поясним практическую целесообразность использования приведенных теорем. Пусть, например, объект состоит из двух структурных блоков, причем порядок каждого блока n = 5. Тогда общее число уравнений состояния объекта равно 10 и, следовательно, матрица A имеет 100 элементов. В то же время матрица A для каждого отдельного блока имеет только по 25 элементов, т. е. в 4 раза меньше. Отсюда ясно, что двукратное использование критерия Калмана при Если передаточная функция объекта имеет хотя бы один нуль, равный ее полюсу, то объект не может быть одновременно полностью управляемым и полностью наблюдаемым. Поэтому внешним признаком такой неполной управляемости или наблюдаемости является наличие одинаковых операторных полиномов в числителе и знаменателе передаточной функции объекта.
2.6.4 Управляемость и наблюдаемость типовых Утверждение 1. Идеальное интегрирующее звено, апериодические звенья первого и второго порядков, а также колебательное звено полностью управляемы и наблюдаемы при любых численных значениях их параметров. В справедливости данного утверждения легко убедиться путем непосредственного применения критериев Калмана об управляемости и наблюдаемости к уравнениям состояния перечисленных звеньев. Утверждение 2. Безынерционное усилительное звено полностью управляемо и наблюдаемо при любых значениях его коэффициента усиления. Для данного звена нельзя записать уравнение состояния, поэтому доказательством утверждения может служить простое рассуждение. Последовательное соединение этого звена и, например, апериодического звена первого порядка эквивалентно тоже апериодическому звену первого порядка, но с другим коэффициентом усиления. Поскольку согласно утверждению 1 новое апериодическое звено полностью управляемо и наблюдаемо, то из выполнимости необходимых условий теоремы 2 следует, что безынерционное усилительное звено формально тоже является полностью управляемым и наблюдаемым. Утверждение 3. Реальное дифференцирующее звено со статизмом G (p) = kT 0 p /(Tp +1) полностью управляемо и наблюдаемо при любых значениях его параметров. Доказательство аналогично выше приведенному. Эквивалентом указанного звена является параллельное соединение безынерционного усилительного звена и апериодического звена первого порядка, поэтому из утверждений 1, 2 и теоремы 1 следует справедливость данного утверждения. Утверждение 4. Реальное дифференцирующее звено без статизма G (p) = k (T 0 p +1)/(Tp +1), T 0 > T полностью управляемо и наблюдаемо при любых значениях его параметров. Если рассматриваемое звено G 1(p) = k (T 0 p +1)/(Tp +1) параллельно соединить с апериодическим звеном первого порядка G 2(p) = k /(Tp +1), то получим реальное дифференцирующее звено со статизмом G 3(p) = kT 0 p /(Tp +1). Поэтому из утверждения 3 и теоремы 1 следует справедливость утверждения 4. Утверждение 5. Идеальное дифференцирующее звено полностью управляемо и наблюдаемо. Последовательное соединение указанного звена и апериодического звена первого порядка эквивалентно реальному дифференцирующему звену без статизма, которое согласно утверждению 4 полностью управляемо и наблюдаемо. Поэтому из утверждения 1 и теоремы 2 очевидна справедливость данного утверждения. Замечание. Управляемость и наблюдаемость — это свойство не самого объекта (или системы), а его математической модели в виде уравнений состояния. При одном выборе переменных состояния обеспечивается полная управляемость, а при другом — полная наблюдаемость. Эти проблемы возникают, если модель объекта представлена дифференциальным уравнением. Понятия управляемости и наблюдаемости важны, например, тогда, когда алгоритм управления формируется не в зависимости от ошибки системы, а в функции переменных состояния: u = u (x 1,..., xn). Однако в изложенном выше смысле они не всегда совпадают с практическими представлениями. Даже если какая-либо переменная состояния и может быть вычислена по доступным для измерения выходным величинам, обработка этих величин, особенно при наличии помех, может быть сложной. Поэтому практически наблюдаемыми переменными обычно считаются те из них, которые могут быть непосредственно измерены теми или иными датчиками.
Идентификация объектов Аналитические методы исследования опираются на математические модели объекта и элементов системы управления. Эти модели получают на основе законов физики, механики, химии и т. д. Такой подход дает положительный результат, если рассматриваемый объект достаточно прост по структуре и хорошо изучен. Если же объект изучен недостаточно или же настолько сложен, что аналитическое описание его математической моделью практически невозможно, прибегают к экспериментальным методам. В этом случае производится статистическая обработка результатов испытаний, по которым «восстанавливается» модель «черного ящика». Может быть использован и экспериментально-аналитический метод, когда априорная модель, полученная аналитическим путем, уточняется в соответствующих экспериментах. Откуда взять модель системы, если отсутствует описание некоторых ее элементов? Для этого выполняется идентификация системы или ее отдельных подсистем. Различают два типа идентификации: структурную и параметрическую. При структурной идентификации определяют структуру реального объекта управления в виде математической модели. После того как математическая модель объекта определена, проводят параметрическую идентификацию, заключающуюся в определении числовых параметров математической модели по экспериментальным данным. Задачу параметрической идентификации можно сформулировать следующим образом. Пусть имеется полностью наблюдаемый и полностью управляемый объект, задаваемый в общем случае уравнениями состояния вида
где B – n -мерный вектор–столбец; C – n -мерный вектор–строка, Целью идентификации является определение элементов матриц А, В, С. Структурная схема объекта представлена на рис. 2.60. На схеме приняты следующие обозначения: u, y – наблюдаемые входной и выходной сигналы; x – ненаблюдаемая (скрытая) переменная, оцениваемая косвенно по сигналам u и y, получаемым в результате преобразования в системе операторами А, В и H; е1, е2 – ненаблюдаемые помехи (случайные процессы типа белого шума); f, v – ненаблюдаемые помехи (коррелированные во времени случайные сигналы, в некоторых случаях содержащие детерминированные составляющие); A, B, C, E, G, H – операторы, вид которых известен, но неизвестны параметры.
Рис. 2.60. Структурная схема объекта параметрической оптимизации Основными постановками задач идентификации являются: – идентификация, или определение характеристик объекта (по значениям u и y определить операторы А, В и C); – генерация случайных сигналов с заданными характеристиками, или определение характеристик сигналов (по значениям f или v определить оператор E или G, H); – наблюдение за скрытыми переменными, или определение переменных состояния (по наблюдаемым u и y, известным операторам A, B, C, E, G, H определить x). Существуют различные методы параметрической оптимизации. В одном случае непосредственно определяются коэффициенты передаточной функции или уравнения объекта. Вторая группа методов используется для определения временных или частотных характеристик объектов, а также характеристик случайных процессов генерируемых объектами. По полученным характеристикам затем определяются передаточная функция или уравнения объекта.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.81.94 (0.28 с.) |
 путем приложения допустимого управления U (t). Объект, обладающий указанным свойством, называется полностью управляемым. Оценка управляемости должна выполняться перед тем, как переходить к оптимизации управляемой системы. Дело в том, что для не полностью управляемого объекта такая задача может оказаться неразрешимой.
путем приложения допустимого управления U (t). Объект, обладающий указанным свойством, называется полностью управляемым. Оценка управляемости должна выполняться перед тем, как переходить к оптимизации управляемой системы. Дело в том, что для не полностью управляемого объекта такая задача может оказаться неразрешимой. . Объект, обладающий таким свойством, называется полностью наблюдаемым. Оценка наблюдаемости объекта должна предшествовать постановке задачи его идентификации, так как не полностью наблюдаемый объект не может быть идентифицирован.
. Объект, обладающий таким свойством, называется полностью наблюдаемым. Оценка наблюдаемости объекта должна предшествовать постановке задачи его идентификации, так как не полностью наблюдаемый объект не может быть идентифицирован.


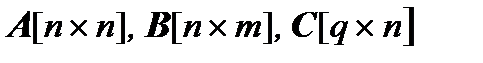 – постоянные матрицы коэффициентов.
– постоянные матрицы коэффициентов. . (2.67)
. (2.67) .
.

 , подаваемое на двигатель, выходом – угловое положение вала нагрузки
, подаваемое на двигатель, выходом – угловое положение вала нагрузки  Величина
Величина  является возмущением (момент нагрузки).
является возмущением (момент нагрузки).



 . В нашем случае n = 2, m = 1 (две переменные состояния и один управляющий сигнал).
. В нашем случае n = 2, m = 1 (две переменные состояния и один управляющий сигнал). .
. принимает вид
принимает вид  :
: .
. можно обеспечить любые значения угла поворота
можно обеспечить любые значения угла поворота  и угловой скорости wд =
и угловой скорости wд =  вала двигателя.
вала двигателя.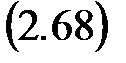

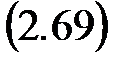




 Критерий полной управляемости по выходу в общем случае имеет вид
Критерий полной управляемости по выходу в общем случае имеет вид

 можно обеспечить любые значения выхода (углового положения нагрузки).
можно обеспечить любые значения выхода (углового положения нагрузки).













