
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система единиц физических величинСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ В МЕТРОЛОГИЮ
ОБЩИЕ ПОЛОЖЕНИЯ
Многие виды деятельности связаны с измерениями физических величин. Физическая величина – характеристика объекта или явления общая в качественном отношении для многих объектов или явлений и индивидуальная в количественном отношении для каждого объекта или явления. Например, масса, присуща многим объектам, но каждый объект обладает определенной массой, отличной от массы других объектов. То же самое можно сказать о скорости движения тел, температуре, объеме и многих других величинах, характеризующих явления. Количественная определенность физической величины называется ее размером, а оценка размера в виде некоторого числа единиц величины называется ее значением. Единица величины – физическая величина фиксированного размера, которой условно присвоено значение – единица, предназначенная для количественной оценки однородных физических величин. Различают истинное и действительное значения физической величины. Истинное значение – такое значение размера физической величины, которое идеально характеризует ее в количественном и качественном отношениях. Оно неизвестно. В философии истинному значению соответствует понятие об абсолютной истине. На практике применяется действительное значение физической величины. Это значение физической величины, найденное опытным путем и настолько близкое к истинному значению, что применяется вместо него в данной измерительной задаче. Действительное значение физической величины устанавливается измерением. Измерение – определение значения физической величины опытным путем с помощью специальных технических средств, называемых средствами измерений. Усовершенствованием измерений занимается наука, называющаяся метрологией. Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. Единство измерений – состояние измерений, когда их результаты выражаются в узаконенных единицах величин, а погрешности измерений с заданной вероятностью не выходят за установленные границы. Единство измерений обеспечивается в пределах государства. В связи с усиливающейся интеграцией мировой экономики оно должно обеспечиваться и на международном уровне. Для этого усилиями многих государств созданы международные метрологические организации: Международная организация мер и весов (МОМВ) и Международная организация законодательной метрологией (МОЗМ).
МОМВ создана в 1975 г. в соответствии с Метрической конвенцией, подписанной 17 странами, в том числе и Россией. В настоящее время к конвенции присоединилось 47 государств, в которых сосредоточено около 95% мирового промышленного капитала. Высшим органом МОМВ, решающим все главные вопросы, является Генеральная конференция по мерам и весам, которая проводится один раз в четыре года. Она избирает международный комитет мер и весов (МКМВ), который руководит МОМВ в периодах между генеральными конференциями. Постоянным действующим органом является международное бюро мер и весов (МБМВ), которое находится во Франции в г. Севре. Оно ведет научно-исследовательскую работу, разрабатывает нормативные и руководящие документы, является хранителем некоторых международных эталонов. В 1955 г. создана Международная организация законодательной метрологии (МОЗМ), целью которой является международное согласование деятельности государственных метрологических служб стран, входящих в МОЗМ. Высшим органом МОЗМ является Международная конференция законодательной метрологии, созываемая один раз в четыре года. Исполнительным органом МОЗМ является Международный комитет законодательной метрологии (МКЗМ), который решает главные вопросы на его заседаниях, проводимых один раз в два года. На постоянной основе в МОЗМ работает международное бюро законодательной метрологии (МБЗМ), которое находится в Париже. Руководит им директор бюро. МБЗМ является хранителем всех документов МОЗМ. В России метрология находится в ведении федеральной службы по техническому регулированию и метрологии. Все отношения в РФ в области метрологии регулируются законом РФ "Об обеспечении единства измерений", на основе которого разрабатываются, применяются и действуют государственные и национальные стандарты в области измерений, составляющих Государственную систему измерений (ГСИ). Частью метрологии является законодательная метрология. Это область метрологии, в которой правила и нормы устанавливаются государством, и оно ведет контроль и надзор за их соблюдением. Область законодательной метрологии в РФ определена законом "Об обеспечении единства измерений".
ИЗМЕРЕНИЯ
Измерение – определение значения физической величины опытным путем с помощью специальных технических средств. Измерения классифицируются по следующим признакам. 1. По способу получения измерительной информации: прямые, косвенные, совокупные и совместные. Прямые измерения - это измерения, при которых искомое значение определяется непосредственно из опытных данных по показаниям средств измерения. Косвенные измерения - это измерения, при которых значение искомой величины находят по результату прямого измерения другой величины, используя зависимость между искомой и измеряемой величинами. Например, нахождение диаметра вала d на основе измерения длины его окружности L, используя зависимость Совокупное измерение, при котором значения одноименных искомых величин находят на основе результатов измерения их комбинаций путем решения системы уравнений. Применяется с целью уменьшения погрешности измерения. Например, необходимо измерить массы х 1, х 2, х 3 трех предметов, значения которых близки к цене деления средства измерения. Измеряют три раза в следующих сочетаниях Решив систему, получим х 1 = 3, х 2 = 4, х 3 = 5 Совместное измерение, при котором последовательно измеряют несколько разноименных величин, с целью нахождения зависимости между ними или значение какой-либо величины. Например, чтобы определить плотность вещества, надо измерить его объем V и массу m, затем вычислить плотность 2. По характеру измеряемой величины: статические и динамические. Статическое измерение – измерение физической величины, принятой неизменяющейся в связи с тем, что скорость реакции средства измерения превышает скорость изменения измеряемой величины. Динамическое изменение – измерение изменяющейся величины, когда скорость изменения измеряемой величины превосходит скорость реакции прибора. 3. По области применения: технические и метрологические. Технические измерения – измерение величины с целью определения их значений. Метрологические измерения – измерение величины, относящейся к средствам измерения, с помощью эталонов с целью определения метрологических характеристик средств измерения. Технические измерения производятся на производстве, в лабораториях технических измерений; метрологические – в метрологических лабораториях. 4. По повторяемости: однократные и многократные. Однократное измерение – измерение физической величины один раз. Многократное измерение – следующие друг за другом измерения одной и той же величины. Технические измерения чаще всего однократные, а метрологические – всегда многократные. 5. По точности: равноточные и неравноточные. Равноточные, выполненные на одном или нескольких средствах измерения одинаковой точности в одинаковых условиях. Неравноточные, выполненные на средствах измерения разной точности в разных условиях. 6. По характеру взаимодействия с объектом измерения: контактные и бесконтактные. Контактное измерение, при котором в процессе измерения имеется механический контакт средства измерения с измеряемой поверхностью объекта измерения.
Бесконтактный, при котором отсутствует вышеуказанный контакт. 7. По отношению к измеряемой величине: абсолютные и относительные. Абсолютное, при котором значение измеряемой величины определяется на основе прямого измерения этой величины. Относительное измерение, при котором значение измеряемой величины определяется на основе измерения отклонений ее от известной величины. Например, измерение размеров деталей с помощью измерительных головок. 8. По методу измерения: непосредственные, сравнения с мерой, нулевой метод, метод замещения. Непосредственное измерение, при котором значение величины определяется непосредственно по показаниям прибора. Нулевой метод, при котором производится сравнение с мерой, и результирующий эффект воздействия измеряемой величины доводят до нуля. Например, взвешивание на рычажных весах с помощью гирь, когда результат равен сумме значений гирь. Метод сравнения, при котором измеряемую величину сравнивают с мерой. Например, взвешивание на стрелочных весах с помощью гирь. Метод замещения – метод сравнения с мерой, при котором измеряемую величину замещают известной величиной, воспроизводимой мерой. КАЧЕСТВО ИЗМЕРЕНИЯ
Характеризуется погрешностью измерения, сходимостью и воспроизводимостью результатов измерения. Погрешность измерения – отклонение результата измерения от истинного значения, в качестве которого на практике применяется результат измерения величины на более точном приборе. Сходимость результатов измерения – это близость результатов многократных измерений, выполненных на одном приборе в одних и тех же условиях. Воспроизводимость результатов измерений – близость результатов измерений, выполненных на разных приборах в разных условиях, но приведенных к нормальным условиям измерения.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Классифицируются по следующим признакам. 1. По характеру проявления: систематические, случайные, дрейфовые и грубые. Систематические – погрешности, постоянные по значению или изменяющиеся по определенному закону, известному или неизвестному. Случайные погрешности, изменяющиеся случайным образом при многократных измерениях одного и того же объекта или величины. Дрейфовые – медленно изменяющиеся во времени случайные погрешности. Грубые – погрешности, резко выделяющиеся среди других при многократных измерениях. 2. По форме представления: абсолютные, относительные и приведенные. Абсолютная погрешность D - разность между результатом измерения х и истинным значением измеряемой величины х и. Она выражается в единицах физической величины и имеет знак + или -. D = х - х и.
Относительная погрешность – отношение абсолютной погрешности к результату измерения. Она часто выражается в %. Приведенная погрешность – отношение абсолютной погрешности к определенному значению х N, в качестве которого принимается длина шкалы средства измерения, выраженная диапазоном показаний шкалы либо длиной шкалы в мм. 3. По источнику происхождения: инструментальные, субъективные, методические и внешние. Инструментальная погрешность – погрешность средства измерения, обусловленная его техническим несовершенством. Субъективная – это погрешность, происходящая от человека – оператора, производящего измерения. Она обусловлена его квалификацией, прилежностью и другими его качествами. 4. Внешние погрешности происходят от несоблюдения нормальных условий измерения, нормированные национальным стандартом, в котором указаны номинальные значения влияющих величин с предельными отклонениями. Влияющая величина – физическая величина, не подлежащая измерению данным средством измерения, но влияющая на результат измерения. В зависимости от принципа действия средства измерения устанавливаются влияющие величины и их предельные значения, зависящие от необходимой точности измерения. Для измерения геометрических величин установлены национальным стандартом России следующие значения влияющих величин, определяющих нормальные условия измерения: температура окружающей среды 20°С, давление 101625 Па, относительная влажность 60%. Последние две величины имеют значение для пневматических средств измерения. Для электрических средств измерения к вышеуказанным следует добавить предельные значения напряженности окружающих магнитного и электрических полей и др. В связи с вышеизложенным различают основную и дополнительную погрешности измерений. Основная погрешность – это погрешность, возникающая при соблюдении нормальных условий измерения. Дополнительная погрешность – это погрешность, обусловленная отклонениями влияющих величин от их предельных значений. Дополнительная погрешность является систематической и, как правило, может быть установлена и учтена поправкой. Так, несоблюдение стандартной температуры при измерении размера детали d приводят к дополнительной погрешности, определяемой по зависимости D = d [aд (Qд - 20) - aи (Qи - 20)], где aд и aи - соответственно коэффициенты линейного расширения материалов измеряемой детали и средства измерения; Qд и Qи - их температуры в градусах в момент измерения детали. Методическая погрешность заложена в самом методе измерения. Например, измерение диаметра вала посредством измерения длины его окружности по зависимости 5. По зависимости погрешности от результата измерения погрешности измерений делятся на аддитивные, мультипликативные и нелинейные.
Аддитивная погрешность постоянная и не зависит от результата измерения Мультипликативная линейно зависит от результата измерения по формуле D = a + bx, где a и b - постоянные числа, x - результат измерения. Нелинейная погрешность связана с результатами измерения нелинейной функцией (рис.1.1).
Р и с. 1.1. Зависимости аддитивной (а), мультипликативной (б) и нелинейной абсолютных погрешностей от результатов измерения х
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Обусловлены совокупностью случайных, малозаметных причин неизвестного происхождения. Они обнаруживаются только при многократных измерениях одного и того же объекта. Предсказать случайные погрешности невозможно. Однако оценить их на основе многократных измерений можно всегда. При этом с определенной вероятностью можно определить пределы и интервалы изменения случайной погрешности. Однако распределение значений случайной погрешности внутри интервала ее изменения может подчиняться различным законам в зависимости от вида объекта измерения. Наибольшее распространение имеет закон нормального распределения при количестве измерений или погрешностей, превышающих Среди случайных погрешностей могут оказаться грубые, резко отличающиеся по значению от остальных. Случайные погрешности подлежат математической обработке с целью исключения грубых погрешностей и определения интервала ее изменения. Рассмотрим методику математической обработки на следующем примере. Учитывая, что метрологические измерения всегда являются многократными и число измерений обычно не превышают десяти, следует применить закон распределения Стьюдента. Пусть при измерении с помощью микрокатора с ценой деления шкалы Обработку производят в следующем порядке. 1. Определяют среднее арифметическое значение погрешности
где n – число измерений. 2. Определяют остаточные погрешности для всех результатов измерений 3. Определяют среднеквадратическую погрешность результатов измерения
4. Определяют доверительный интервал с вероятностью 0,95, т.е. с вероятностью 0,05 того, что погрешность измерения не попадет в этот интервал. По прил. 2 для числа степеней свободы n = 6 и вероятности 0,95 находим значение критерия Стьюдента 5. Определяют среднюю квадратическую погрешность для средней арифметической погрешности, т.к. она также является случайной
Для средней арифметической погрешности доверительный интервал определяется
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
Возникают из-за определенных причин, известных или неизвестных. Последние необходимо установить, если это возможно, и, если невозможно, то необходимо определить или оценить возникающую по той или иной причине систематическую погрешность, что является обязательным требованием, предъявляемым к измерениям. Значение систематической погрешности всегда можно определить измерением объекта на более точном приборе или измерением известной величины, например, меры. Систематические погрешности могут быть постоянными или изменяющимися с течением времени при многократных измерениях. Постоянные систематические погрешности можно установить только измерением на более точном приборе. Изменяющиеся систематические погрешности можно установить измерением на более точном приборе или обнаружить многократными измерениями с последующей обработкой результатов измерений методами математической статистики. Известно несколько методов обнаружения изменяющейся систематической погрешности. Рассмотрим два из них, имеющих наибольшее распространение. Метод Аббе – метод последовательных разностей. Применим его к вышерассмотренному примеру. 1. Определим среднюю квадратическую погрешность s2 = 2,822 = 7,95 2. Определим квадраты последовательных разностей по формуле
3. Вычислим критерий Аббе
4. По табл. 1.1 для уровня значимости 0,05 и n = 7 находим табличное значение критерия Аббе Vt = 0,42. Если V > Vt, то отсутствует изменяющаяся систематическая погрешность, иначе она имеется.
Таблица 1.1 Значение критерия Аббе
В нашем случае V > Vt 0,57 > 0,42. Это означает, что среди погрешностей измерения нет изменяющейся систематической погрешности, и это подтверждает сделанный нами ранее вывод. Изменяющуюся систематическую погрешность можно обнаружить методом сравнения средних арифметических значений результатов измерения для группы измерений, выполненных в начале, и группы измерений, выполненных в конце серии многократных измерений. Пусть проведены многократные измерения в последовательности х 1, х 2, … хn. Для обнаружения систематической погрешности необходимо взять 4…6 измерений, проведенных в начале, и столько же измерений, проведенных в конце. По результатам измерений определяют среднее арифметическое значение
Задавшись уровнем значимости a, по таблицам критерия Стьюдента по числу степеней свободы f = n 1 - n 2 - 2 и уровню значимости a определяют значение tt. Если t > tt, то результаты измерения содержат изменяющуюся систематическую погрешность; если t < tt, то результаты измерения не содержат изменяющуюся систематическую погрешность. Пример. Пусть по результатам многократных измерений для пяти первых значений получено
Табличное значение для a = 0,05 и числу степеней свободы Известные систематические погрешности необходимо учитывать. Для этого в результат измерения вводят поправку, которую прибавляют с учетом ее знака к результату измерения. Поправка – систематическая погрешность, взятая с обратным знаком. В метрологии применяются следующие термины: - неисключенная систематическая погрешность – погрешность, не учтенная поправкой в результате измерения; - исключенная систематическая погрешность – это та, которая учтена поправкой. Результат измерения, в котором учтена поправка, называется исправленным, если в результате измерения поправка не учтена, то он называется неисправленным.
МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
Результат косвенного измерения у определяется по зависимости ее от величин х 1, х 2, …, хn, измеренных прямыми измерениями. В общем виде это может быть записано так у = f (х 1, х 2, …, хn) В метрологических измерениях аргументы – величины х 1, х 2, …, хn подвергаются многократным прямым измерениям. Результат измерения каждой из них определяется их математической обработкой. В общем случае результаты измерения могут содержать как случайные, так и систематические погрешности. Если они известны заранее, то в результаты прямых измерений вначале вводят поправки – получают исправленные результаты измерений, которые в дальнейшем рассматриваются как случайные. Часто известен предел допустимой погрешности средства измерения данного типа, но конкретное значение систематической погрешности данного средства измерения неизвестно, которое может принимать значения от -q до +q и поэтому может рассматриваться как случайная величина, изменяющаяся в этих пределах. В связи с тем, что для конкретного средства измерения и конкретного измерения конкретное значение систематической погрешности неизвестно, а известны ее предельные значения, то результаты многократных измерений каждой величины следует рассматривать как случайные, вариации которых обусловлены только случайными причинами, и закон распределения принимается равномерным. Вначале производят обработку результатов многократных измерений согласно вышеуказанной методике (см.1.6). Для каждой величины х 1, х 2, …, хn определяют среднее арифметическое значение
Среднее арифметическое значение
Доверительные границы случайной погрешности результата измерения определяются e = ± t s y где t – коэффициент Стьюдента, определяемый по прил.2. Для доверительной вероятности Р, значение которой принимают в зависимости от допустимой степени риска из ряда 0,95, 0,98, 0,99 и числу степеней свободы, определяемому выражением
где ni - число прямых измерений величины хi. В общем случае на результат измерения оказывают влияние несколько систематических погрешностей, конкретные значения которых, как правило, неизвестны, а известны их предельные значения. Составляющими неисключенной систематической погрешности могут быть погрешности средства измерения, оцениваемые пределами ±q; погрешности от влияния внешних условий (температуры, напряженности магнитного и электрических полей, влажности, давления и др.). При этом известны пределы изменения систематических погрешностей, обусловленные влиянием внешних условий и других причин. Влияние их на результат измерения оценивается пределами результирующей неисключенной систематической погрешности, определяемой по зависимости
где q j – результирующая неисключенная систематическая погрешность прямых многократных измерений величины хi, определяемая в зависимости от доверительной вероятности по зависимости
К и Кj - коэффициенты, которые зависят от принятой доверительной вероятности и принимают значение К = 1,1 при Р = 0,95, К = 1,4 при Р = 0,99. К относится к результату измерения у, а Кj - к результату прямого измерения величины хi; т – количество неисключенных систематических погрешностей для прямого измерения величины хi. В зависимости от соотношения e и q можно принять следующие решения: 1) при у = где n – среднее число многократных измерений для величин х 1, х 2, …, хn; 2) при у = 3) при у = D = К e + q Ниже рассмотрен конкретный пример обработки результатов косвенного измерения сопротивления электрической цепи и мощности тока.
ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ Таблица 1.2
1. Обработка результатов прямых измерений напряжения 1.1. Определяем среднее арифметическое значение
1.2. Определяем остаточные погрешности результатов измерения и их квадраты
1.3. Определяем среднее квадратическое отклонение результатов измерения SU = 1.4. Определяем критерий Стьюдента t (см. прил.2) для заданной вероятности 0,95 и числа степеней свободы k = n - 1 = 6-1 = 1.5. Определяем границы доверительного интервала случайной погрешности измерения D U = t × SU = 2,57 × 4,26 = 10,9 В Среди результатов измерений нет таких, для которых Если среди результатов измерений имеются грубые (для которых |D Ui | > D U), то их следует вычеркнуть и пункты с 1.1 по 1.5 выполнить с оставшимися результатами. 1.6. Определяем среднее квадратическое отклонение для результата измерения, т.е. для среднего арифметического значения
1.7. Определяем результирующее значение для неисключенной систематической погрешности (для Р = 0,95 k = 1,1) q U = 1.8. Определяем отношение При U = При U = При 0,8 < bU = ± kU d U где В рассматриваемом случае
bU = ± 2,19 × 2,88 = ± 6,3 1.9. Результат измерения напряжения U = 104,83 ± 6,3 В, Р = 0,95, n = 6. Таблица 1.3
bR = ± 0,74 (2,57 × 0,6 + 2) = ± 3,02 3.8. Результат косвенного измерения сопротивления: R = 7,58 ± 3,02 Ом, P = 0,95, n = 6. 4. Обработка результатов косвенных измерений мощности по зависимости W = I × U
4.1. Среднее значение WI = 4.2. Среднее квадратическое отклонение результатов косвенного измерения мощности
4.3. Определяем число степеней свободы f 1 = Для Р = 0,95 f 1 = 6 t = 2,45 (cм. прил. 2). 4.4. Граница случайной погрешности измерения мощности D W = t 4.5. Граница неисключенной систематической погрешности измерения мощности
4.6. Определяем отношение 4.7. Определяем границу суммарной погрешности измерения мощности bW = ± k 3 (D W + q W) По табл. 1.3 для bW = ± 0,74 (306,25 + 137,49) = ± 328,37 Вт 4.8. Результат косвенного измерения мощности: W = 1450 ± 328,37 Вт, Р = 0,95, n = 6. СРЕДСТВА ИЗМЕРЕНИЯ (СИ)
Эталоны Занимают особое место среди СИ, так как без них обеспечить единство измерения невозможно. Эталон - СИ, предназначенное для воспроизведения и хранения размера единицы величины, дольных или кратных ее значений, с целью передачи размера другим средствам измерения этой величины. Воспроизведение единицы физической величины – совокупность операций по материализации единицы величины с помощью эталона более высокой точности или с помощью специальных устройств. Хранение единицы величины – совокупность операций, обеспечивающих постоянство во времени размера величины, присущего данному средству измерения. Передача размера единицы величины – приведение размера единицы величины, хранимой данным средством измерения, к размеру воспроизводимому или хранимому эталоном. По точности и применению эталоны делятся на следующие виды: - первичный эталон – эталон, воспроизводящий размер единицы величины с наивысшей точностью; - вторичный – эталон, который хранит и воспроизводит размер единицы величины путем сличения с первичным эталоном. По существу – это копия первичного эталона; - эталон-копия – это вторичный эталон, предназначенный для передачи размера единицы величины рабочим эталонам; - рабочий эталон, применяемый для передачи размера единицы величины рабочим средствам измерения; - исходный эталон – это эталон, принятый в качестве первичного в данной метрологической службе; - эталон сравнения – вторичный эталон, применяемый для сличения эталонов, которые не могут быть сличены не
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.74.100 (0.015 с.) |

 .
.
 .
. .
. содержит методическую погрешность, зависящую от того, сколько знаков после запятой взято в числе p.
содержит методическую погрешность, зависящую от того, сколько знаков после запятой взято в числе p.
 мкм
мкм : d1 = 0; d2 = 1; d3 = -1; d4 = -3; d5 = -4; d6 = 2; d7 = 5.
: d1 = 0; d2 = 1; d3 = -1; d4 = -3; d5 = -4; d6 = 2; d7 = 5. мкм
мкм мкм
мкм мкм. Результат метрологического измерения записывают в следующей стандартной форме
мкм. Результат метрологического измерения записывают в следующей стандартной форме , n = 7, p = 0,95
, n = 7, p = 0,95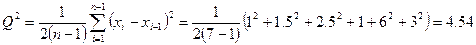

 и дисперсию
и дисперсию  для измерений, проведенных в начале, и эти же величины
для измерений, проведенных в начале, и эти же величины  и
и 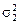 для измерений, проведенных в конце. По этим величинам и числу измерений n 1 и n 2 вычисляют критерий t.
для измерений, проведенных в конце. По этим величинам и числу измерений n 1 и n 2 вычисляют критерий t.
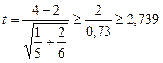
 и его дисперсию
и его дисперсию 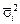 . Среднее квадратическое отклонение результата косвенного измерения величины у определяется:
. Среднее квадратическое отклонение результата косвенного измерения величины у определяется:
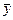 определяется:
определяется:
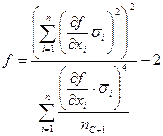
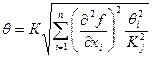
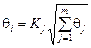 ;
; случайная погрешность ничтожна по сравнению со систематической и ею можно пренебречь, учитывается только систематическая погрешность. Результат измерения записывают
случайная погрешность ничтожна по сравнению со систематической и ею можно пренебречь, учитывается только систематическая погрешность. Результат измерения записывают , n = …, P = …
, n = …, P = … систематическая погрешность ничтожна и ею можно пренебречь, q» 0. Результат измерения записывают
систематическая погрешность ничтожна и ею можно пренебречь, q» 0. Результат измерения записывают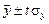 , n = …, P = …,
, n = …, P = …,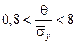 пренебрегать случайной и систематической погрешностями нельзя. Результат измерения записывают
пренебрегать случайной и систематической погрешностями нельзя. Результат измерения записывают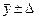 , n = …, P = …
, n = …, P = …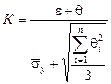
 В
В = - 4,83
= - 4,83
 90,84 В
90,84 В В
В В
В В
В .
.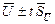
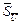 » 0, и результат измерения записывают так:
» 0, и результат измерения записывают так: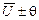
 ,
,  .
.

 В
В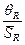
 = 13,83 . 104,83 = 1450 Вт
= 13,83 . 104,83 = 1450 Вт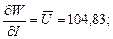
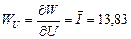
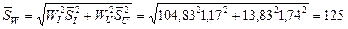 Вт
Вт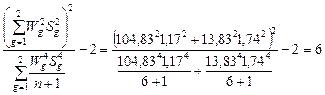
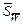 = 2,45 . 125 = 306,25 Вт
= 2,45 . 125 = 306,25 Вт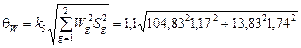 = 137,49 Вт
= 137,49 Вт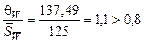 . Нельзя пренебрегать ни случайной, ни систематической погрешностями.
. Нельзя пренебрегать ни случайной, ни систематической погрешностями.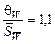 и Р = 0,95 k 3 = 0,74.
и Р = 0,95 k 3 = 0,74.


