Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов косвенныхСодержание книги
Поиск на нашем сайте
МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
Результат косвенного измерения у определяется по зависимости ее от величин х 1, х 2, …, хn, измеренных прямыми измерениями. В общем виде это может быть записано так у = f (х 1, х 2, …, хn) В метрологических измерениях аргументы – величины х 1, х 2, …, хn подвергаются многократным прямым измерениям. Результат измерения каждой из них определяется их математической обработкой. В общем случае результаты измерения могут содержать как случайные, так и систематические погрешности. Если они известны заранее, то в результаты прямых измерений вначале вводят поправки – получают исправленные результаты измерений, которые в дальнейшем рассматриваются как случайные. Часто известен предел допустимой погрешности средства измерения данного типа, но конкретное значение систематической погрешности данного средства измерения неизвестно, которое может принимать значения от -q до +q и поэтому может рассматриваться как случайная величина, изменяющаяся в этих пределах. В связи с тем, что для конкретного средства измерения и конкретного измерения конкретное значение систематической погрешности неизвестно, а известны ее предельные значения, то результаты многократных измерений каждой величины следует рассматривать как случайные, вариации которых обусловлены только случайными причинами, и закон распределения принимается равномерным. Вначале производят обработку результатов многократных измерений согласно вышеуказанной методике (см.1.6). Для каждой величины х 1, х 2, …, хn определяют среднее арифметическое значение
Среднее арифметическое значение
Доверительные границы случайной погрешности результата измерения определяются e = ± t s y где t – коэффициент Стьюдента, определяемый по прил.2. Для доверительной вероятности Р, значение которой принимают в зависимости от допустимой степени риска из ряда 0,95, 0,98, 0,99 и числу степеней свободы, определяемому выражением
где ni - число прямых измерений величины хi. В общем случае на результат измерения оказывают влияние несколько систематических погрешностей, конкретные значения которых, как правило, неизвестны, а известны их предельные значения. Составляющими неисключенной систематической погрешности могут быть погрешности средства измерения, оцениваемые пределами ±q; погрешности от влияния внешних условий (температуры, напряженности магнитного и электрических полей, влажности, давления и др.). При этом известны пределы изменения систематических погрешностей, обусловленные влиянием внешних условий и других причин. Влияние их на результат измерения оценивается пределами результирующей неисключенной систематической погрешности, определяемой по зависимости
где q j – результирующая неисключенная систематическая погрешность прямых многократных измерений величины хi, определяемая в зависимости от доверительной вероятности по зависимости
К и Кj - коэффициенты, которые зависят от принятой доверительной вероятности и принимают значение К = 1,1 при Р = 0,95, К = 1,4 при Р = 0,99. К относится к результату измерения у, а Кj - к результату прямого измерения величины хi; т – количество неисключенных систематических погрешностей для прямого измерения величины хi. В зависимости от соотношения e и q можно принять следующие решения: 1) при у = где n – среднее число многократных измерений для величин х 1, х 2, …, хn; 2) при у = 3) при у = D = К e + q Ниже рассмотрен конкретный пример обработки результатов косвенного измерения сопротивления электрической цепи и мощности тока.
ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.006 с.) |

 и его дисперсию
и его дисперсию 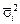 . Среднее квадратическое отклонение результата косвенного измерения величины у определяется:
. Среднее квадратическое отклонение результата косвенного измерения величины у определяется:
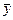 определяется:
определяется:
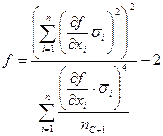
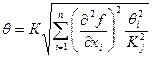
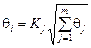 ;
; случайная погрешность ничтожна по сравнению со систематической и ею можно пренебречь, учитывается только систематическая погрешность. Результат измерения записывают
случайная погрешность ничтожна по сравнению со систематической и ею можно пренебречь, учитывается только систематическая погрешность. Результат измерения записывают , n = …, P = …
, n = …, P = … систематическая погрешность ничтожна и ею можно пренебречь, q» 0. Результат измерения записывают
систематическая погрешность ничтожна и ею можно пренебречь, q» 0. Результат измерения записывают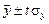 , n = …, P = …,
, n = …, P = …,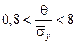 пренебрегать случайной и систематической погрешностями нельзя. Результат измерения записывают
пренебрегать случайной и систематической погрешностями нельзя. Результат измерения записывают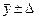 , n = …, P = …
, n = …, P = …