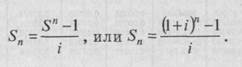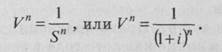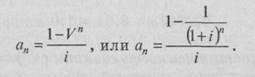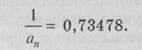Элементы финансовой математики

Для анализа обоснованности финансирования инвестиций в недвижимость, при определении залоговой стоимости объектов с учетом доходно­го подхода необходимо применять элементы фи­нансовой математики. При расчете нормы дохо­да на инвестируемый капитал должна учитывать­ся текущая стоимость будущих доходов для со­поставимости с текущей стоимостью инвестиций, иначе будущие доходы в случае их преобразова­ния в текущую стоимость могут оказаться рав­ными капитальным вложениям.

Для анализа денежных потоков от недвижи­мости, определения текущей стоимости инвести­ций, обоснования величины платы за получение будущих потоков дохода широко применяются функции сложных процентов.

Сложный процент – процент, начисленный на основную сумму долга и невыплаченные ранее проценты, начисленные за предыдущий период.

Пример. 100 тыс. р. положены под 10% годовых. Рассчитаем сумму депозита (суммы на банковском счету) по простому и сложному про­центу, если период накопления 4 года.

Расчет суммы депозита по простому и сложному проценту

 

Параметры	Сложный %	Простой %
Депозит, тыс. р.
Начисления на конец первого года, тыс. р.
Депозит на начало второго года, тыс. р. Начисления на конец года, тыс. р.		110 10
Депозит на начало третьего года, тыс. р. Начисления на конец года, тыс. р.	121 12,1	120 10
Депозит на начало четвертого года, тыс. р. Начисления на конец года, тыс. р.	133,1 13,31	130 10
Депозит на конец четвертого года, тыс. р.	146,41

 

Основные функции сложного процента: 1) бу­дущая стоимость единицы; 2) накопление едини­цы за период; 3) фактор фонда возмещения; 4) текущая стоимость единицы; 5) текущая сто­имость единичного аннуитета; 6) взнос за амор­тизацию денежной единицы.

Для определения этих функций и удобного при­менения в работе с различными потоками доходов используют финансовые калькуляторы. Они име­ют клавиши числа периодов, периодической став­ки процента, периодического платежа, текущей стоимости суммы, будущей стоимости суммы и др. Для упрощения расчетов в случае отсутствия фи­нансового калькулятора применяют таблицы слож­ных процентов (см. пример табл. 3.1, 3.2).

Рассмотрим перечисленные выше функции сложного процента.

Будущая стоимость единицы (Sn) – будущая стоимость одной денежной единицы через п пе­риодов при ставке сложного процента i.

 

 

где Sn - сумма после п периодов; i – периодическая фактическая ставка процента; п – число периодов.

Таблица 3.1 20,00%

6 ФУНКЦИЙ (начисление процентов ежегодно)

 

№ Будущая года стоимость единицы	Накопление единицы за период	Фактор фонда возмещения	Текущая стоимость единицы	Текущая стоимость единично­го аннуи­тета	Взнос на амортиза­цию еди­ницы	№ года
1 1.20000 2 1.44000 3 1.72800 4 2.07360 5 2.48832 6 2.98598 7 3.58318 8 4.29982 9 5.15978 10 6.19174 11 7.43008 12 8.91610 13 10.69932 14 12.83919 15 15.40702 16 18.48843 17 22.18611 18 26.62333 19 31.94800 20 38.33760 21 46.00512 22 55.20615 23 66.24738 24 79.49685 25 95.39622 26 114.47547 27 137.37056 28 164.84467 29 197.81361 30 237.37633 31 284.85160 32 341.82192 33 410.18630 34 492.22357 35 590.66828 36 708.80194 37 850.56233 38 1020.67480 39 1224.80976 40 1469.77171	1.00000 2.20000 3.64000 5.36800 7.44160 9.92992 12.91590 16.49908 20.79890 25.95868 32.15042 39.58050 48.49660 59.19592 72.03511 87.44213 105.93056 128.11667 154.74000 186.68801 225.02561 271.03073 326.23688 392.48425 471.98111 567.37733 681.85280 819.22336 984.06803 1181.88164 1419.25797 1704.10957 2045.93149 2456.11779 2948.34136 3539.0096 4247.81158 5098.37391 6119.04870 7343.8584	1.00000 0.45455 0.27473 0.18629 0.13438 0.10071 0.07742 0.06061 0.04808 0.03852 0.03110 0.02526 0.02062 0.01689 0.01388 0.01144 0.00944 0.00781 0.00646 0.00536 0.00444 0.00369 0.00307 0.00255 0.00212 0.00176 0.00147 0.00122 0.00102 0.00085 0.00070 0.00059 0.00049 0.00041 0.00034 0.00028 0.00024 0.00020 0.00016 0.00014	0.83333 0.69444 0.57870 0.48225 0.40188 0.33490 0.27908 0.23257 0.19381 0.16151 0.13459 0.11216 0.09346 0.07789 0.06491 0.05409 0.04507 0.03756 0.03130 0.02608 0.02174 0.01811 0.01509 0.01258 0.01048 0.00874 0.00728 0.00607 0.00506 0.00421 0.00351 0.00293 0.00244 0.00203 0.00169 0.00141 0.00118 0.00098 0.00082 0.00068	0.83333 1.52778 2.10648 2.58873 2.99061 3.32551 3.60459 3.83716 4.03097 4.19247 4.32706 4.43922 4.53268 4.61057 4.67547 4.72956 4.77463 4.81219 4.84350 4.86958 4.89132 4.90943 4.92453 4.93710 4.94759 4.95632 4.96360 4.96967 4.97472 4.97894 4.98245 4.98537 4.98781 4.98984 4.99153 4.99295 4.99412 4.99510 4.99592 1.99660	1.20000 0.65455 0.47473 0.38629 0.33438 0.30071 0.27742 0.26061 0.24808 0.23852 0.23110 0.22526 0.22062 0.21689 0.21388 0.21144 0.20944 0.20781 0.20646 0.20536 0.20444 0.20369 0.20307 0.20255 0.20212 0.20176 0.20147 0.20122 0.20102 0.20085 0.20070 0.20059 0.20049 0.20041 0.20034 0.20028 0.20024 0.20020 0.20016 0.20014	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

Таблица 3.2 30,00%

6 ФУНКЦИЙ (начисление процентов ежегодно)

№ Будущая года стоимость единицы	Накопление единицы за период	Фактор фонда возмеще­ния	Текущая стои­мость единицы	Текущая стоимость единичного аннуитета	Взнос на аморти­зацию единицы	№ года
1 1.30000 2 1.69000 3 2.19700 4 2.85610 5 3.71293 6 4.82681 7 6.27485 8 8.15731 9 10.60450 10 13.78585 11 17.92161 12 23.29809 13 30.28751 14 39.37377 15 51.18590 16 66.54167 17 86.50417 18 112.45543 19 146.19205 20 190.04967 21 247.06458 22 321.18395 23 417.53914 24 542.80089 25 705.64116 26 917.33352 27 1 1 92.53359 28 1550.29368 29 2015.38180 30 2619.99636 31 3405.9953 32 4427.7939 33 5756.13217 34 7482.97189 35 9727.8636 36 12646.2227 37 16440.0897 38 21372.1168 39 27783.7521 40 36118.8781	1.00000 2.30000 3.99000 6.18700 9.04310 12.75603 17.58284 23.85769 32.01500 42.61950 56.40535 74.32696 97.62504 127.91256 167.28633 218.47223 285.01390 371.51807 483.97350 630.16555 820.21522 1067.27980 1388.46375 1806.00289 2348.8038 3054.445 3971.77847 5164.31206 6714.60573 8729.9875 11349.9839 14755.9792 19183.7731 24939.905 32422.877 42150.7408 54796.964 71237.0532 92609.1700 120392.922	1.00000 0.43478 0.25063 0.16163 0.11058 0.07839 0.05687 0.04192 0.03124 0.02346 0.01773 0.01345 0.01024 0.00782 0.00598 0.00458 0.00351 0.00269 0.00207 0.00159 0.00122 0.00094 0.00072 0.00055 0.00043 0.00033 0.00025 0.00019 0.00015 0.00011 0.00009 0.00007 0.00005 0.00004 0.00003 0.00002 0.00002 0.00001 0.00001 0.00001	0.76923 0.59172 0.45517 0.35013 0.26933 0.20718 0.15937 0.12259 0.09430 0.07254 0.05580 0.04292 0.03302 0.02540 0.01954 0.01503 0.01156 0.00889 0.00684 0.00526 0.00405 0.00311 0.00239 0.00184 0.00142 0.00109 0.00084 0.00065 0.00050 0.00038 0.00029 0.00023 0.00017 0.00013 0.00010 0.00008 0.00006 0.00005 0.00004 0.00003	0.76923 1.36095 1.81611 2.16624 2.43557 2.64275 2.80211 2.92470 3.01900 3.09154 3.14734 3.19026 3.22328 3.24867 3.26821 3.28324 3.29480 3.30369 3.31053 3.31579 3.31984 3.32295 3.32535 3.32719 3.32861 3.32970 3.33054 3.33118 3.33168 3.33206 3.33235 3.33258 3.33275 3.33289 3.33299 3.33307 3.33317 3.33318 3.33321 3.33324	1.30000 0.73478 0.55063 0.46163 0.41058 0.37839 0.35687 0.34192 0.33124 0.32346 0.31773 0.31345 0.31024 0.30782 0.30598 0.30458 0.30351 0.30269 0.30207 0.30159 0.30122 0.30094 0.30072 0.30055 0.30043 0.30033 0.30025 0.30019 0.30015 0.30011 0.30009 0.30007 0.30005 0.30004 0.30003 0.30002 0.30002 0.30001 0.30001 0.30001	1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

 

Пример. Необходимо определить будущую стоимость 1 000 000 рублей при ставке сложного процента 30%, если период накопления составит 5 лет.

 

1 000 000 х (1+0,3)5 = 3 712 930 р.

 

Используем для решения этой задачи табли­цы сложных процентов. Инвестор, зная стоимость одного рубля к концу пятого года накопления, может узнать будущую стоимость одного милли­она рублей, умножив будущую стоимость одного рубля на вложенную сумму:

 

1 000 000 х 3,71293 = 3 712 930 р.

 

То есть при инвестировании 1 млн р. при став­ке 30 % к концу пятого года стоимость вложен­ных средств составит 3,71 млн р.

Накопление единицы за период (Sn) – оста­ток денежных средств через п периодов при став­ке сложного процента, равной i, в результате пе­риодического пополнения основной суммы депо­зита за счет новых взносов и перевода накоплен­ных процентов в основную сумму депозита.

 

 

Пример. При вкладе на 3 года рубль, депо­нированный в конце первого года, будет прино­сить процент в течение 2 лет; рубль, депониро­ванный в конце второго года, – в течение одного года; рубль, депонированный в конце третьего года, не принесет процента.

Фактор фонда возмещения (SFF) – показы­вает денежную сумму, которую необходимо депо­нировать в конце каждого периода для того, что­бы через п периодов при ставке сложного про­цента i остаток на счете составил один рубль.

 

 

Периодический платеж = Желаемая сумма х x SFF.

Пример. Если остаток на депозите прино­сит ежегодно 20 % дохода, то для того, чтобы за три года накопить 3, 64 млн р., нужно ежегодно вкладывать по 1 млн р.:

0,27473 х 3,64 = 1,0 млн р.

Текущая стоимость единицы (Vn) – текущая стоимость одной денежной единицы, которая дол­жна быть получена через п периодов при ставке сложного процента, равной i.

 

 

Вследствие того, что целью инвестирования является получение доходов в будущем, важным шагом в оценке является определение текущей стоимости реверсии.

Текущая стоимость реверсии – это текущая стоимость денежных единиц, которые должны быть получены в будущем. Стоимость денег из­меняется во времени, стоимость одного рубля в будущем меньше его стоимости сегодня.

Пример. При 20% -и ставке дисконта теку­щая стоимость 1 млн р., ожидаемого к получе­нию через год, составит 833 тыс. р.:

Vn = l/(1+0,2)1= 0,833; 0,833 х 1,0 = 833 тыс.р.

Текущая стоимость единичного аннуитета (ап) – текущая стоимость серии ожидаемых рав­ных единичных поступлений в течение n перио­дов при ставке сложного процентам.

 

 

При заданной ставке дисконта текущая сто­имость аннуитета может быть рассчитана в ре­зультате оценки каждого платежа как отдельной реверсии.

Пример. Право получения 100 тыс. р. дохода в конце каждого года в течение следующих 3 лет можно оценить следующим обра­зом:

аn= 2,106, 100 х 2.106 = 210,6 тыс.р.

Следовательно, текущая стоимость инвестиций 210,6 тыс. р. является обоснованной платой за право получения 100 тыс. руб. в конце каждого следующего года в течение 3 лет при 20% - й став­ке.

Взнос на амортизацию денежной единицы – коэффициент частичных платежей, который по­казывает величину обязательного периодического платежа, необходимую для погашения кредита за п периодов при ставке сложного процентам

 

 

Амортизация денежной единицы – это про­цесс погашения долга в течение определенного времени. Взнос на амортизацию кредита матема­тически определяется как отношение одного пла­тежа к первоначальной сумме кредита.

Пример. Ожидается получить 1 тыс. р. в конце каждого из двух последующих лет при го­довой ставке 30%.

Отношение одного платежа к основной сумме кредита показывает размер периодического пла­тежа, необходимого для погашения долга, кото­рый для одного рубля в данном случае составит:

 

 

Следовательно, для полного погашения перво­начальной суммы кредита и процентов, начисленных по годовой ставке 30 %, в конце каждого года на протяжении 2 лет следует за каждую 1 тыс. р. уплачивать 734,8 тыс. р.