Тема 4. Олимпиады, конкурсы, турниры по математике для младших школьников

 

Цель: познакомиться с таким видом внеурочной деятельности по математике, как олимпиада; решать задачи, предлагаемые младшим школьникам на олимпиадах.

 

Занятие 1 (4 ч). Организационные вопросы проведения математических олимпиад для младших школьников

 

Литература: [3], [9], [13] из списка основной литературы, [18] – из списка дополнительной литературы.

 

Вопросы для обсуждения

1. Какими документами должен руководствоваться учитель при проведении математических олимпиад разного уровня?

2. Каково содержание примерного положения о школьной предметной олимпиаде?

3. Как вы оцениваете примерное положение об олимпиаде по математике в начальной школе, содержащееся в книге: Дик Н. Ф. 1000 олимпиадных заданий по математике в начальной школе. – Ростов-н./Д.: Феникс, 2008?

4. Как составлять олимпиадные задания по математике для младших школьников? Каким требованиям они должны удовлетворять? Как их оценивать?

5. Можно ли использовать положения статьи: Фарков А. Многоуровневые олимпиады // Народное образование. – 2004. – № 1. – С. 151–156 – при проведении олимпиад в начальной школе?

6. Надо ли готовить младших школьников к математическим олимпиадам? Если надо, то как это делать?

7. Где можно найти информацию о конкурсах и олимпиадах для младших школьников?

 

Решение задач олимпиадного характера

Задание. Решите задачи и назовите эвристический прием, которым могут воспользоваться младшие школьники, решая данные задачи.

1. Нужно перевезти 540 тонн угля на трех машинах. За сколько дней это можно сделать, если на каждую машину грузить по три тонны и делать пять поездок в день?

Сколькими способами вы можете решить эту задачу?

2. Журавли часто летают так, что образуют правильный треугольник: впереди один журавль (вожак), за ним 2, потом 3 журавля и т. д. Сколько летело в стае журавлей, если в последнем ряду их было 8? А если было 28?

3. На уроке математики Мальвина предложила своим ученикам записать четыре различных числа от 10 до 20 и сложить их. Какие это были числа, каждый ученик придумывал сам.

- Мой ответ – 75, – сказал Пьеро.

- Вы ошиблись, – возразила Мальвина, даже не взглянув на его пример.

Почему она так решила, ведь чисел Пьеро она не знала?

(Дружинин Б.А. и др. Путешествие в мир учения. 2 уровень, ч. 2, с. 14)

4. Петя живет в квартире, номер которой 200. На его этаже есть еще три квартиры. Какие номера могут быть у этих квартир? (Из статьи Останиной Е. Е. Начальная школа. – 2009. – № 4)

Занятие 2 (4 ч). Математические олимпиады для учащихся начальной школы

Литература:[3] – из списка основной литературы;

• Положение о Всероссийском Интеллектуальном марафоне учеников-занковцев (сайт www.zankov.ru);

• Международная олимпиада школ РО // Начальная школа. – 2008. – № 15 (приложение к газете «Первое сентября»);

• Положение о Международном математическом конкурсе-игре «Кенгуру» (www.kenguru.sp.ru).

 

Вопросы для обсуждения

1. Каковы особенности Всероссийского интеллектуального марафона учеников-занковцев (этапы, содержание, оценивание результатов)?

2. Выполните задания по математике, которые были предложены на II туре (2007/2008 уч. год) марафона:

а) В корзине лежат грецкие орехи. Если эти орехи считать по два, по три, по пять или по семь, то в каждом случае в корзине будет оставаться один лишний орех. Известно также, что орехов меньше 300. Сколько орехов в корзине?

б) Папа, мама и двое детей собираются сесть в автомобиль, в котором 4 места (включая водительское). Сколькими способами они могут разместиться в автомобиле, если за руль может сесть только кто-нибудь из взрослых?

в) Нина купила в школьном буфете 7 конфет. Оля купила 5 конфет. Во дворе к ним подошла Юля, и девочки решили разделить конфеты между собой поровну. Юля отдала подругам за конфеты 24 рубля. Как должны разделить между собой эти деньги Нина и Оля по справедливости?

3. Каковы особенности Международной олимпиады школ развивающего обучения (система Д. Б. Эльконина – В. В. Давыдова)?

4. Выполните задания по математике, которые были предложены на Международной олимпиаде для 2 класса (первый тур, 2008 г.).

а) Переставь местами цифры в числе 73029, чтобы полученное число было как можно меньше.

б) Машина бабушка родилась 29.09.1955. Маша заметила, что в записи этой даты сумма первых четырех цифр равна сумме последних четырех. Сколько лет исполнилось бабушке при последующем таком совпадении?

в) На рисунке изображены числа

Запиши их друг за другом в таком порядке, чтобы получившееся число было как можно больше.

5. Каковы особенности Международного математического конкурса-игры «Кенгуру» (краткая история, организация, правила оформления работ)?

6. Решите задачи для 3–4 классов конкурса «Кенгуру», который проводился в 2009 году. За какое время вы сможете это сделать?

 

Задачи, оцениваемые в 3 балла

1. Сколько треугольников на рисунке 25?

(А) 2 (Г) 5	(Б) 3 (В) 4 (Д) 6

2. 200 ´ 9 + 200 + 9 =?

(А) 418 (Б) 1909 (В) 2009

(Г) 4018 (Д) 20009

 

3. Сколько всего вершин у четырех кубиков?

(А) 32 (Б) 24 (В) 16 (Г) 12 (Д) 4

 

4. Где кенгуру?

(А) В круге и треугольнике, но не в квадрате. (Б) В круге и в квадрате, но не в треугольнике. (В) В треугольнике и в квадрате, но не в круге. (Г) Не в треугольнике и не в квадрате, но в круге. (Д) Не в круге и не в треугольнике, но в квадрате.

5. В пятиэтажном доме в каждом подъезде на каждом этаже расположено по 4 квартиры. На каком этаже находится квартира с номером 71?

(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

6. На клетчатой бумаге нарисовано число 930 (см. рисунок). Сколько маленьких квадратиков должно поменять цвет, чтобы получилось число 806?

(А) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9

7. Вася подсчитал число дней в двух идущих подряд месяцах. Какое число он не мог получить?

(А) 62 (Б) 60 (В) 58 (Г) 59 (Д) 61

8. Шоколадная плитка состоит из одинаковых долек. Маленький Владик разделил ее «по-честному»: сначала он отломал полоску из 5 долек для бабушки, а затем полоску из 7 долек для дедушки (см. рисунок). Сколько долек у него осталось?

(А) 23 (Б) 28 (В) 30 (Г) 35 (Д) 40

9. Произведение цифр двузначного числа не может равняться

(А) 40 (Б) 36 (В) 20 (Г) 13 (Д) 12

10. В 3 часа ночи в замке появилось Привидение. Часы на башне замка, которые до этого показывали правильное время, пошли с обычной скоростью, но в другую сторону. Привидение исчезло с рассветом, в 4 часа 45 минут. Какое время в этот момент показывали часы?

(А) полночь (Б) 1 ч 15 мин (В) 1 ч 30 мин

(Г) 2 ч 15 мин (Д) 7 ч 45 мин

 

Задачи, оцениваемые в 4 балла

11. В танцевальной студии занимались 25 мальчиков и 19 девочек. Каждую неделю в группу приходят два новых мальчика и три новых девочки. Через сколько недель мальчиков и девочек в этой студии станет поровну?

(А) 6 (Б) 5 (В) 4 (Г) 3 (Д) 2

12. У скольких трехзначных чисел сумма цифр равна 2?

(А) 0 (Б) 1 (В) 2 (Г) 3 (Д) 4

13.

На картинке справа изменили цвет каждой клеточки: белый – на красный и наоборот. Что получилось?

14. В комнате сидят несколько кошек и собак. Кошачьих лап в комнате вдвое больше, чем собачьих носов. Тогда кошек в комнате

(А) вдвое больше, чем собак (Б) столько же, сколько собак

(В) вдвое меньше, чем собак (Г) в 4 раза меньше, чем собак

(Д) в 4 раза больше, чем собак

15. Город разделен улицами на квадратные кварталы. Машина выезжает из точки М и на каждом перекрестке поворачивает налево или направо. Проехав один квартал, машина повернула направо, потом три раза налево, а потом еще два раза направо. На каком из рисунков изображен маршрут машины?

16. Белки Анни, Элли и Салли нашли вместе семь орехов. Каждая из них нашла хотя бы по одному ореху, и у всех оказалось разное число орехов. Алли нашла орехов меньше всех, а Элли – больше всех. Сколько орехов нашла Элли?

(А) 4 (Б) 3 (В) 2 (Г) 1

(Д) невозможно определить

17. Аня и Петя живут на набережной. Слева от дома Ани на набережной находится 47 домов, а справа – 23 дома. От дома Пети слева и справа по набережной находится одинаковое число домов. Сколько домов расположено между домами Ани и Пети?

(А) 10 (Б) 11 (В) 12 (Г) 13 (Д) 14

18. Из палочек можно выкладывать цифры, как на рисунке. Какова сумма цифр самого большого числа, которое удастся выложить, использовав ровно 15 палочек?

(А) 5 (Б) 15 (В) 27 (Г) 35 (Д) 45

19. Букет состоит из 4 цветков: красного, голубого, желтого и белого. Пчела Майя садится на каждый цветок в букете только один раз. Она начинает с красного цветка и не перелетает с желтого сразу на белый. Сколькими способами Майя может облететь все цветы?

(А) 6 (Б) 4 (В) 3 (Г) 2 (Д) 1

20. Будем называть шестизначное число счастливым, если у него сумма цифр, стоящих на нечетных местах, равна сумме цифр, стоящих на четных местах. В каком случае можно заполнить пустые места цифрами так, чтобы получилось счастливое число?

Задачи, оцениваемые в 5 баллов

21.

Какую фигуру нельзя составить из двух костяшек домино, изображенных на рисунке справа?

22. Дикарь Пятница написал в строчку несколько различных чисел, не превосходящих 10. Робинзон Крузо заметил, что в любой паре соседних чисел одно из них делится на другое без остатка. Какое наибольшее количество чисел мог написать Пятница?

(А) 6 (Б) 7 (В) 8 (Г) 9 (Д) 10

23. В доме между любыми двумя комнатами не более одной двери, и из каждой комнаты не более одной двери ведет в сад. Всего в доме 12 дверей. Какое наименьшее число комнат может быть в этом доме?

(А) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7

24. В таблицу 3´3 вписывают цифры так, что все 6 сумм, полученных при сложении цифр из каждой строки и каждого столбца, оказываются разными. Чему равна самая маленькая сумма всех цифр в таблице с таким свойством?

(А) 7 (Б) 8 (В) 9 (Г) 10 (Д) 12

25. В равенстве К + А + N + G + A + R + O + O = 56 разные буквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры. Наименьшее возможное значение суммы К + А + N равно

(А) 3 (Б) 9 (В) 13 (Г) 17 (Д) 19

26. На рисунке изображены три одинаковых кубика. На гранях кубиков нарисованы цифры: 0, 1, 3, 4, 5, 9. Чему равна сумма чисел на нижних гранях этих кубиков?

(А) 10 (Б) 9 (В) 8 (Г) 7 (Д) 6

 

Задания для самостоятельной работы

1. Напишите об олимпиадах по математике для учащихся 2–4 классов, которые проводятся в школе, где вы работаете. Приведите примеры олимпиадных заданий (с решениями).

2. Решите задачи для 3–4 классов конкурса «Кенгуру», который проводился в 2008 году.

 

Задания, оцениваемые в 3 балла

1. Сколько различных букв в словах УРА КЕНГУРУ?

(А) 7 (Б) 6 (В) 5 (Г) 4 (Д) 3

2. На листе бумаги поставили точку и провели через нее четыре прямые. На сколько частей эти прямые разделили лист бумаги?

(А) 4 (Б) 6 (В) 8 (Г) 10 (Д) 12

3. Через шесть с половиной часов наступит полночь. А сейчас который час?

(А) 21:30 (Б) 6:30 (В) 20:30 (Г) 17:30 (Д) 10:30

4. Сколько веревочек на рисунке?

(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

5. Сколько месяцев имеют в названии ровно 4 буквы?

(А) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6

6. В первом аквариуме на 12 рыбок больше, чем во втором. Сколько рыбок надо переселить из первого аквариума во второй, чтобы рыбок в них стало поровну?

(А) 12 (Б) 8 (В) 6 (Г) 4 (Д) 2

7. Дорожка выложена из 14 квадратных плит со стороной 1 м. Антон отметил центр каждой плиты и соединил эти точки линией. Какую длину имеет эта линия?

(А) 12 м (Б) 13 м (В) 14 м (Г) 15 м (Д) 16 м

8. Какое из этих чисел не равно остальным?

(А) сто раз по двадцать (Б) двадцать сотен

(В) двести десятков (Г) две тысячи

(Д) сто раз по двести

9.

Никита кладет на лист бумаги два одинаковых треугольника (нарисованных справа) и обводит контур полученной фигуры. Какую фигуру он не сможет получить?

10. Какую цифру или знак арифметического действия нужно поставить вместо *, чтобы равенство 1 + 1 * 1 – 2 = 100 стало верным?

(А) + (Б) – (В) ´ (Г) 0 (Д) 1

 

Задачи, оцениваемые в 4 балла

11. Гоша выше Бориса, но ниже Антона. Витя выше Димы, но ниже Гоши. Кто из мальчиков самый высокий?

(А) Антон (Б) Борис (В) Витя (Г) Гоша (Д) Дима

12. Вася любит умножать на 3, Маша – прибавлять 2, а Петя – вычитать 1. В каком порядке детей надо вызвать к доске выполнить любимое действие, чтобы из 1 получить 4?

(А) М, В, П (Б) П, М, В (В) П, В, М

(Г) М, П, В (Д) В, М, П

13. Фигура составлена из 6 спичек.

Сережа переложил две спички. Какая из фигур (А) – (Г) не могла получиться?

(Д) все фигуры могли получиться

14. У Даши 20 кубиков, у Маши 12 кубиков, у Глаши 8 кубиков, а у Наташи – 6 кубиков. Кто из девочек может построить куб из всех своих кубиков?

(А) Даша (Б) Маша (В) Глаша (Г) Наташа (Д) никто не может

15. В некоторой гостинице к приему гостей готово 5 трехместных номеров и один двухместный номер. Сколько еще двухместных номеров надо подготовить, чтобы разместить группу из 25 туристов?

(А) 3 (Б) 4 (В) 5 (Г) 6 (Д) 8

16. Квадратный участок земли разбит на 4 части: газон Г, цветник Ц, огород О и сад С.

 

Сад и цветник – квадраты. Периметр сада – 80 м, а цветника – 20 м. Чему равен периметр газона?

(А) 20 м (Б) 25 м (В) 30 м (Г) 50 м (Д) 100 м

17. В память о своем боевом прошлом старый пират отчеканил по одной монете достоинством 1000 дукатов, 3000 дукатов, 4000 дукатов, 6000 дукатов и 7000 дукатов. Сколькими способами он может набрать из них сумму в 14000 дукатов?

(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

18. Сколько существует двузначных чисел. У который цифра десятков меньше, чем цифра единиц?

(А) 50 (Б) 45 (В) 36 (Г) 18 (Д) 9

19. Конкурс «Кенгуру», в котором ты сегодня участвуешь, проходит в России уже в 15-й раз (всегда в марте). Первый раз Аня участвовала в 11-м конкурсе, когда ей только что исполнилось 10 лет. В каком году она родилась?

(А) 1987 (Б) 1989 (В) 1993 (Г) 1994 (Д) 1998

20. Три юных кенгуренка Кенг, Гур и Ру сидят на весах. Если с весов спрыгнет Кенг, то весы покажут 3 кг. Если спрыгнет Гур, то весы покажут 4 кг, а если спрыгнет Ру, то весы покажут 5 кг. Сколько весят все кенгурята вместе?

(А) 12 кг (Б) 10 кг (В) 8 кг (Г) 7 кг (Д) 6 кг

 

Задачи, оцениваемые в 5 баллов

21. У Тани и ее родителей общий день рождения – 1 января. В январе 2007 года Таня была в 6 раз младше своей мамы, а в январе 2008 – в 6 раз младше папы. На сколько лет папа старше мамы?

(А) 1 (Б) 4 (В) 5 (Г) 6 (Д) 7

22. Точки А, В, С и D отмечены на прямой в некотором порядке. Известны расстояния: от А до В – 13 см, от В до С – 11 см, от С до D – 14 см и от D до А – 12 см. Чему равно расстояние между наиболее удаленными точками?

(А) 14 см (Б) 25 см (В) 27 см (Г) 38 см (Д) 50 см

23. Один странный мальчик по четвергам и пятницам говорит только правду, по вторникам всегда лжет, а в остальные дни недели он может и солгать, и сказать правду. Семь дней подряд мальчика спрашивали, как его зовут. Первые шесть ответов, по порядку, были таковы: Женя, Боря, Вася, Боря, Петя, Боря. Как он ответил на седьмой день?

(А) Женя (Б) Боря (В) Петя (Г) Вася

(Д) невозможно определить

24. Фонтан на площади старинного города связан с часами на башне: он работает, когда хотя бы одна из стрелок часов находится между цифрами 3 и 4 или между цифрами 8 и 9.

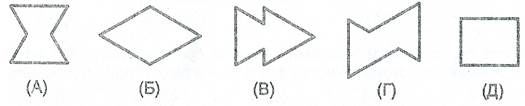
Сколько времени в течение суток этот фонтан работает?

(А) 11 ч 40 мин (Б) 9 ч 30 мин (В) 7 ч 20 мин

(Г) 5 ч 40 мин (Д) 4 ч

25. Из каждой заготовки (А) – (Д) можно склеить кубик. 4 кубика получатся одинаковыми, а один будет от них отличаться. Из какой заготовки получится этот кубик?

26. В первый понедельник каждого из трех летних месяцев Маша записывала число, на которое пришелся этот понедельник, а в конце лета сложила три записанных числа. Какая наименьшая сумма могла получиться?

(А) 3 (Б) 8 (В) 9 (Г) 10 (Д) 12