
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Види простих задач 3-го класу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Учні знайомляться з новими видами простих задач: 12. Задачі на збільшення або зменшення числа у кілька разів. 13. Задачі на кратне порівняння. 14. Задачі на знаходження невідомого множника, діленого, дільника. 15. Задачі на знаходження частини від числа. 16. Задачі на знаходження числа за його частиною. 17. Задачі з пропорційними величинами. 18. Задачі на знаходження периметру многокутника. 19.Задачі на знаходження відстані при русі назустріч. 20. Задачі на час.
Розглянемо деякі задачі визначених видів. 12.Задачі на збільшення або зменшення числа у кілька разів.
1 –
На ступені підготовчої роботи до введення задач даного виду необхідно актуалізувати конкретний зміст дії множення і ділення на рівні частини. А також, засобом спеціальних вправ підвести учнів до усвідомлення конкретного змісту виразів “більше в” та “менше в”, наприклад: 1.Покладіть у рядочок три кружечки. А нижче покладіть два рази по три кружечки. - Де кружечків більше? - Скільки,у другому рядку, разів ми поклали по стільки кружечків, скільки в першому рядку? (Два рази) - Тому говорять, що в другому рядку кружечків в 2 рази більше, ніж в першому. - Де кружечків менше? - У першому рядку лише один раз по 3 кружечки, а в другому – два рази, у другому рядку у 2 рази більше кружечків, ніж в першому. - Тому говорять, що в першому рядку у 2 рази менше кружечків, ніж в другому. - Для того, щоб кружечків стало в 2 рази більше, ніж 3, треба по стільки ж, по 3, взяти 2 рази, або взяти стільки ж – 3 та ще раз стільки ж – 3. 2.Покладіть ліворуч 2 квадрати, а праворуч у 4 рази більше. - Що треба зробити, щоб покласти квадратів у 4 рази більше, ніж 2? (Треба по 2 квадрати взяти 4 рази.) - Де квадратів більше? - У кілька разів праворуч квадратів більше? Чому? (Праворуч квадратів в 4 рази більше, тому що ліворуч лежить лише один раз по 2 квадрати, а праворуч – 4 рази.) - Згадайте, скільки квадратів ми поклали ліворуч? - Як дізнатися скільки квадратів лежить праворуч? (Треба по 2 квадрати взяти 4 рази,тобто 2 помножити на 4, отримаємо 8.) - Якою арифметичною дією дізналися про число квадратів, яке в 4 рази більше за 2? (Дією множення, 2 . 4 = 8.) - Перевірте перерахуванням. - Зробіть висновок. (Для того, щоб дізнатися про число, яке у декілька разів більше за дане, треба дане число помножити на число, яке показує у скільки разів шукане більше за дане. Або: про число, яке у кілька разів більше даного дізнаємося дією множення.) 3.Покладіть у верхньому рядочку 5 трикутників, а під ними покладіть трикутників у 3 рази більше. - Що означає вираз “ у 3 рази більше”? (Цей вираз означає,що у нижньому рядочку треба викласти 3 рази по стільки трикутників, скільки в верхньому рядочку.) - У скільки разів збільшилася кількість трикутників? (У 3 рази.) - Якою дією дізнаємося про кількість трикутників у нижньому рядочку? (Дією множення, 5. 3 = 15.) - Перевірите перерахуванням. - Де трикутників менше? У скільки разів? - Як отримати трикутників “ у 3 рази менше”? (У другому рядку трикутників у 3 раза більше, тобто тут трикутників 3 рази по стільки, скільки повинно бути в верхньому рядку. Треба трикутники, що розташовані в нижньому рядку поділити на 3 рівні частини, отримали по 5 трикутників в кожній. А тепер залишимо лише одну таку частину, і отримаємо трикутників у 3 рази менше.) - Якою дією дізнаємося про число трикутників, яке у 3 рази менше за 15? (Ми ділили трикутники на три рівні частини, тому дією ділення.) - Зробіть висновок (Про число, яке у кілька разів менше за дане дізнаємося дією ділення.) 1. Знайдіть число, яке в 6 раз більше за число 8.Знайдіть число, яке на 6 більше, ніж число 8. 2. Дано число 56.Знайдіть число, яке в 7 разів менше за нього. Знайдіть число, яке на 7 менше,ніж число 56. На підставі 5-го та 6-го завдань, а також аналогічним їм, можна зробити узагальнення: “Більше число знаходимо дією додавання або множення. Додаємо тоді, коли число більше даного на декілька одиниць. Множимо тоді, коли число більше даного у декілька разів. ”; “Менше число знаходимо дією віднімання або ділення. Віднімаємо тоді, коли число менше даного на декілька одиниць. Ділимо тоді, коли число менше даного у декілька разів. ” Такі завдання слід пропонувати учням на декількох попередніх уроках перед вивченням теми “Збільшення та зменшення числа в кілька разів”. Далі учитель пропонує учням накреслити в зошиті відрізок АВ довжиною 3 см, а нижче – відрізок КМ, довжина якого в 4 рази більша за 3 см. При цьому учні міркують так, як і при виконанні практичних завдань на ступіні підготовки: “ Щоб накреслити шуканий відрізок треба по 3 см відкласти 4 рази.”: 3 см
Потім учні знаходять довжину відрізку КМ обчисленням. Учні міркують так: “ Треба по 3 см взяти 4 рази, тобто 3 помножити на 4, 3 . 4 = 12 (см).”.Учитель пропонує учням пояснити числа даної рівності: число 3 – означає довжину відрізка АВ, виражену в сантиметрах, а число 4 – показує у скільки разів відрізок КМ більше відрізка АВ; число 12 – означає довжину відрізка КМ, виражену в сантиметрах. Таким чином, щоб відповісти на запитання задачі “Яка довжина відрізка КМ?” треба знати два числові значення: 1 – довжину відрізка АВ, відомо 3 см, та П – у скільки разів довжина відрізка КМ більша за довжину відрізка АВ, відомо, у 4; відповімо на запитання задачі дією множення, тому що по 3 см треба взяти 4 рази.
3 . 4
Отже, щоб знайти число, яке в 4 рази більше за 3, треба виконати дію множення. Після відповіді на запитання задачі встановлюємо, що знайдене нами число в 4 рази більше даного; ми його отримали збільшивши дане число – 3 у 4 рази. І далі учні читають правило, що наведено в підручнику і виділено курсивом. Підготовка до введення задач на зменшення числа у кілька разів. Школярам пропонується накреслити відрізок, довжиною 12 см, а нижче накреслити відрізок, довжина, якого в 3 рази менша за довжину даного відрізка. При цьому учні міркують так: “Ми не знаємо довжини другого відрізка. Але для його побудови треба знати відстань між його кінцями, ця відстань може бути виражена в сантиметрах або за зразком – еталоном. Із умови задачі відомо, що шуканий відрізок має довжину в 3 рази меншу за 12 см, тому треба відрізок, довжиною 12 см поділити на три рівні частини, одна з яких – еталон. Якщо ми побудуємо відрізок, який має таку саму довжину, що і одна із трьох рівних частин – еталон, то ми отримаємо шуканий відрізок. 12 см
Далі учитель пропонує знайти довжину шуканого відрізка. Учні міркують так: “Шуканий відрізок – це одна із трьох рівних частин цілого відрізка, довжиною 12 см. Для того,щоб знайти довжину однієї такої частини, треба довжину цілого відрізка поділити на кількість рівних частин в ньому: 12: 3 = 4 (см).” Учитель пропонує учням пояснити числа даної рівності: число 12 означає довжину даного відрізка, яка виражена в сантиметрах, число 3 означає у скільки разів довжина шуканого відрізка менше довжини даного, число 4 означає довжину шуканого відрізка, яка виражена в сантиметрах. Таким чином, щоб відповісти на запитання “Чому дорівнює довжина шуканого відрізка?”, треба знати два числові значення: 1 – довжину даного відрізка, відомо 12 см, та П – у скільки разів довжина шуканого відрізка менша за довжину даного відрізка, відомо – у 3 рази; відповімо на запитання задачі дією ділення, тому що шуканий відрізок – це одна з трьох рівних частин даного відрізка.
?
12: 3
Назвавши відповідь, діти з’ясовують, що в результаті отримали число, яке менше за дане в 3 рази; і читають правило, що подано у підручнику курсивом. Ознайомлення з задачами даного виду. Спочатку можна розв’язати задачу відомого дітям виду – на збільшення числа на декілька одиниць з тою самою ситуацією, що описується в задачі. Наприклад: “ Сину 3 років, батько на 24 роки старший. Скільки років батькові?” Учні складають короткий запис цієї задачі і розв’язують її усно. На дошці з’являються записи:
Розв’язання: 3 + 24 = 27 (років) Відповідь: 27 років батькові. Після розв’язання даної задачі учитель пропонує прочитати задачу “ Сину 3 роки, а батько в 9 разів старший. Скільки років батькові?”. Робота над задачею здійснюється згідно узагальненої пам’ятки: 1.Прочитай задачу та уяви про що в ній розповідається. Про що розповідається в задачі? (В задачі розповідається про вік батька та сина. Синові 3 роки, а батько в 9 раз старший, тобто йому в 3 рази більше років, ніж синові. Запитується: “Скільки років батькові?”) - Чим ця задача відмічається від попередньої? (Ця задача відмічається тим, що тут сказано не на скільки років батько старший за сина, а у скільки разів він старший.) Учитель повідомляє, що ця задача нового виду, який має таку опорну схему:
1 –
2.Виділи ключові слова та склади короткий запис задачі. (Ключові слова: “Син”, “Батько”.) Учні складають короткий запис, застосовуючи опорну схему: Син – 3 роки Батько -?, в 9 раз років б. 3.За коротким записом поясни числові дані задачі та запитання. (Число 3 означає вік сина, виражений в роках; число 9 означає у скільки разів більше вік батька, ніж вік сина.) 4.Повтори запитання задачі. Що потрібно знати, щоб на нього відповісти? (Запитується “ Скільки років батькові?”. Для того щоб відповісти на це запитання треба знати два числові значення: 1 – вік сина, відомо – 3 роки, та П – у скільки разів вік батька більше за вік сина, відомо – в 9 разів.) Якою арифметичною дією відповімо на запитання? (Відповімо на запитання задачі дією множення: щоб знайти число, яке у кілька разів більше даного, треба дане число помножити на число, яке показує у скільки разів шукане більше за дане число.) Чи можна відразу відповісти на запитання задачі? (Можна, тому що нам відомі обидва числові значення.):
?
3 , 9 7. Запиши розв’язання задачі. Розв’язання: 3. 9 = 27 (років) Запиши відповідь. Відповідь: 27 років батькові.
Всі записи на дошці здійснюються таким чином, щоб учням було зручно проводити порівняння коротких записів і розв’язків цих двох задач. Спочатку учні знаходять спільне в умовах даних задач і їх розв’язаннях: в обох задачах описується одна й та сама ситуація, вік сина однаковий, батько старший за сина, однакове запитання – “Скільки років батькові?”; ми отримали одне й те саме число у відповіді. Потім учні встановлюють відмінності: в першій задачі сказано, що батькові на 24 роки більше,ніж синові; а в другій задачі сказано, що йому в 9 разів років більше, ніж синові; таким чином в задачах подані різні умови стосовно віку батька, які визначають вибір відповідно різних арифметичних дій: додавання і множення. Методику ознайомлення з задачами на зменшення числа у декілька разів можна скласти аналогічно розглянутій попереду. А можна, перетворити задачу на збільшення числа у декілька разів у задачу на зменшення числа у кілька разів; порівняти умови і розв’язання цих задач і узагальнити, що в цих задачах визначає вибір арифметичної дії: якщо шукане число більше даного у кілька разів, то його знаходять дією множення; якщо шукане число менше даного у кілька разів, то його знаходять дією ділення. Результатом порівняння таких задач може бути узагальнення:
13. Задачі на кратне порівняння.
Методикою введення нового виду задач передбачено підготовчу роботу, метою якої є засвоєння правила: щоб знайти у скільки разів одне число більше або менше за інше число, треба більше число поділити на менше число. Можна запропонувати учням накреслити в зошитах два відрізки, один під другим: АВ = 2 см і КМ = 10 см; і запитати: - Який відрізок має більшу довжину, довший? - У скільки разів довжина відрізка КМ більша за довжину відрізка АВ? Як про це дізнатися? - Як би ми міркували, якщо довжина відрізка КМ була б невідомою, а дано у скільки разів він довший за відрізок АВ? (Ми би по 2 см (довжині відрізка АВ) відклали би стільки разів, у скільки КМ довший за АВ.) - А це обернене завдання, тут треба дізнатися саме, про те скільки разів по 2 см вміщується у довжині відрізка КМ - в 10 см. Як про це дізнатися? (Треба від початку відрізка КМ відкласти 2 см, потім ще 2 см, і так далі, доки не дістанемо кінця відрізку КМ; і підрахувати скільки разів по 2 см вміщується в 10 см (довжині відрізка КМ).) - Якщо ми дізнаємося скільки разів вміщується, то яку арифметичну дію слід обрати для цього? (Дію ділення) - Як обчисленням дізнатися у скільки разів довжина відрізка КМ – 10 см більша за довжину відрізку АВ – 2 см? Тобто, якою арифметичною дією дізнаємося у скільки разів число 10 більше за число 2? (Дією ділення, треба 10 поділити на 2.) Таким чином, щоб дізнатися у скільки разів одне число більше за інше, треба більше поділити на менше число. - Який відрізок коротший? (АВ) У скільки разів відрізок АВ коротший за відрізок КМ? (В 5 разів, тому що відрізок КМ в 5 разів довший за АВ, тому відрізок АВ також в 5 разів коротший за АВ.) - Як обчисленням дізнатися у скільки разів відрізок АВ коротший за відрізок КМ? Як дізнатися у скільки разів число 2 менше за число 10? (Дізнаємось так само, як дізнавалися про те у скільки разів число 10 більше числа 2 – треба число 10 поділити на 2.) Таким чином, щоб дізнатися у скільки разів одне число менше за інше треба більше число поділити на менше. - Порівняйте ці два правила, що в них спільного? (В них спільне те, що в обох випадках треба більше число поділити на менше число.) - Об’єднайте ці два правила в одне. (Для того, щоб дізнатися у скільки разів одне число більше, або менше за друге, треба більше число поділити на менше.) Л.Н.Скаткіним сформульовані вимоги щодо ознайомлення учнів з кратним порівнянням: 1.Перше ознайомлення необхідно провести практично, пропонуючи дітям безпосередньо порівняти довжину відрізків різного розміру, а потім перейти до порівняння числових значень величини (що було реалізовано нами). 2.Обидва питання “ У скільки разів більше?”, “У скільки разів менше?” слід розглядати разом, тому що прийом кратного порівняння при цьому один і той самий. 3.Далі слід перейти до кратного порівняння кількостей, ілюструючи це порівняння на класній рахівниці. 4.Після цього можна перейти до порівняння чисел, які означають значення інших величин: вартості, віку й тощо, а потім – до кратного порівняння відлучених чисел. Правила кратного порівняння можна також ввести на підставі додаткових завдань до задач на збільшення або зменшення числа у декілька разів. Наприклад, перевіряючи домашню задачу “ Маса індика 15 кг, а гуски – в 3 рази менше. Яка маса гуски?”, можна запропонувати додаткові запитання: - Яка маса індика?(15 кг) - Яка маса гуски? (5 кг) - Маса якої птиці менша?(Менша маса гуски) - У скільки разів маса гуски менша,ніж маса індика?(У 3 рази) - У скільки разів маса індика більша маси гуски? (У стільки ж, у 3 рази) - Як ви про це дізналися?(В умові задачі, яку ми розв’язали сказано, що маса гуски в 3 рази менша, ніж маса індика.) - Як можна про це дізнатися обчисленням? Яку дію слід виконати між числами 15 та 5,щоб отримати 3?(В результаті ми отримали менше число; менше число знаходимо відніманням або діленням; очевидно, віднімання не підходить, томі що при зменшенні 15 на 5 ми не отримаємо 3. Таким чином, про це можна дізнатися дією ділення: 15: 5 = 3.) - Щоб дізнатися у скільки разів одне число більше другого, що ми зробили?(Ми більше число поділили на менше.) - Який висновок можна зробити про те, як знайти у скільки разів одне число більше ніж друге число?(Щоб знайти у скільки разів одне число більше другого, треба більше число поділити на менше) - На скільки маса індика більше маси гуски? Якою дією відповімо на це запитання? На скільки маса гуски менша маси індика? (Для того,щоб дізнатися на скільки одне число більше другого, треба від більшого числа відняти менше число: 15 – 5 = 10 (кг) – на 10 кг маса індика більша маси гуски. На стільки ж маса гуски менша маси індика.) Для закріплення правила кратного і різницевого порівняння Л.Н.Скаткін пропонує завдання для усної лічби за таблицею:
Ознайомлення з задачами на кратне порівняння можна здійснити засобом перетворення задачі на збільшення або зменшення числа у декілька разів. Такий методичний прийом допоможе учням побачити відмінності цих двох видів задач. Наприклад, можна запропонувати таку задачу: “ Гуска важить 3 кг, а порося в 5 разів більше. Скільки важить порося?” Учні складають короткий запис цієї задачі і розв’язують її усно:
Розв’язання. 3 . 5 = 15 (кг) Виписуємо числа задачі і пояснюємо їх: 3, 5, - пряма задача.
Потім учитель пропонує учням скласти обернену задачу до даної, так щоб невідомим було число 5, яке означає у скільки разів порося важче за гуску.
Складаємо задачу “ Маса гуски 3 кг, а мас порося 15 кг. У скільки разів порося важче за гуски?”. Таким чином, складена учнями задача – це задача нового виду, спосіб розв’язування таких задач учні повинні засвоїти на даному уроці. Школярі встановлюють чим відрізняється ця задача від попередньої: в першій задачі відомо у скільки разів порося важче за гуска, а в другій – про це запитується. Учитель показує опорну схему до задач даного виду: 
П –
Далі робота над задачею здійснюється за узагальненою пам’яткою. Учні розповідають про що говориться в задачі; складають короткий запис, виділяючи ключові слова і застосовуючи опорну схему; пояснюють числа задачі і називають запитання. Зазначимо, що називаючи запитання задачі просимо школярів переформулювати його, наприклад “ У скільки разів маса поросяти більше за масу гуски?”.Наведемо лише аналітичний пошук розв’язування задачі: - Що треба знати, щоб відповісти на запитання задачі “ У скільки разів маса поросяти більша за масу гуски?”? (Треба знати два числові значення: 1 – масу поросяти, відомо – 15 кг, та П – масу гуски, відомо – 3 кг.) - Якою арифметичною дією відповімо на запитання задачі? (Дією ділення, щоб дізнатися у скільки разів одне число більше за друге, треба більше поділити на менше число.) - ?
15: 3
Записавши розв’язання і відповідь до задачі,учні відповідають на запитання “У скільки разів маса гуски менша за масу поросяти?”, а потім порівнюють умови і розв’язання даної і попередньої задачі. Ці задачі взаємо обернені, вони мають різну математичну структуру, що наочно видно на короткому записі: у задачах на порівняння відомі обидва числа, а запитання показується круглою дужкою. Розв’язуються ці задачі різними діями: перша – множенням; друга – діленням. Між тим, якщо б в першій задачі була дана маса поросяти – 15 кг, а про масу гуски було б сказано,що вона у 5 разів менша за масу поросяти, то така задача розв’язувалась би дією ділення; і ці задачі мали б однакові розв’язки, але від цього вони не стали б задачами однієї математичної структури. Далі можна обговорити з учнями питання про те, на які задачі схожий короткий запис задач на кратне порівняння; які задачі на порівняння ми вже вміємо розв’язувати; чим відмічаються їх короткі записи. І після цього можна перейти до другого запитання “ На скільки кілограмів гуска легша за порося?”: складаємо короткий запис, записуємо розв’язок задачі і відповідь на дошці. Учні порівнюють задачі на кратне і різницеве порівняння. Л.Н.Скаткін пропонує звернути увагу дітей на вірний запис найменувань під час розв’язання таких задач, наприклад: 80 см – 40 см = 40 см Відповідь: на 40 см зелена смужка коротша за червону. 80 см: 40 см = 2 Відповідь: в 2 рази зелена смужка коротша за червону. Усвідомленню математичного змісту задач на кратне порівняння сприяють завдання на складання задач цього виду, та задач на різницеве порівняння і на збільшення або зменшення числа у декілька разів, які
14.Задачі на знаходження невідомого множника, діленого, дільника. Задачі на знаходження невідомого множника.
В 3-му класі діти познайомилися з новим способом розв’язування задач – способом рівняння. Задачі даного виду пропонується розв’язувати способом складання рівняння. Таким чином, на ступені підготовчої роботи учні повинні вивчити правило знаходження невідомого множника, на підставі якого розв’язуються найпростіші рівняння на знаходження невідомого множника. З цією метою, учні виконують завдання, в яких з кожного прикладу на множення треба скласти два приклади на ділення, і на підставі, вже добре відомого їм, взаємозв’язку множення і ділення, роблять два висновки:
=:
Познайомити учнів з правилом знаходження невідомого множника можна на підставі аналогії. З цією метою актуалізуємо знання в учнів про дію додавання і дію множення, і пропонуємо учням порівняти ці дії, при цьому вони міркують таким чином “ Множення – це додавання однакових доданків значить, множення – це особливий випадок додавання; тому ці дії подібні, тобто особливості, які притаманні дії додавання також можуть мати місце і при множенні; наприклад, переставна властивість притаманна і додаванню і множенню; обидва числа при додаванні і при множенні носять однакові назви: випадку додавання – доданки, у випадку множення – множники. Відрізняються тим, що додавання перевіряється відніманням, а множення – діленням.”. Таким чином, на цій підставі можна припустити, що правилу знаходження невідомого доданка існує аналогічне правило для знаходження невідомого множника, але треба взяти до уваги, що додавання перевіряється відніманням, а множення - діленням.Учитель пропонує перебудувати правило на знаходження невідомого доданка в правило на знаходження невідомого множника (у таблиці замінюємо відповідні слова):
Потім учні перевіряють вірність припущення за аналогією на конкретних прикладах, і роблять висновок. Ознайомлення. Наведемо методику роботи над задачею: “ Невідоме число помножили на 4 і отримали 28. Знайди невідоме число.”. З способом складання рівняння учні познайомилися на прикладі задачі на знаходження невідомого доданка і працювали, за пам’яткою: 1. Прочитай задачу та уяви про що в ній розповідається. 2. Поясни,що означають числа задачі. 3. Поясни, що є шуканим в задачі. 4. Познач невідоме число буквою, наприклад – х. 5. Виділи зв’язки невідомого з іншими числовими даними задачі. Склади рівняння. 6. Розв’яжи рівняння. Зроби перевірку. 7. Дай відповідь на запитання задачі. Задачу будемо розв’язувати за даною пам’яткою. - Прочитай задачу та уяви про що в ній розповідається. Про що йде мова в задачі? (В задачі говориться про невідоме число, яке помножили на 4 й отримали 28) - Поясни,що означають числа задачі. Що означає число 4? (Це означає,що невідоме помножили на 4, тому 4 –це другий множник.) Що означає число 28? (Число 28 означає скільки дістали після множення, тобто це добуток.) - Що є шуканим в задачі? (Шуканим є число, яке невідоме.) - Позначимо невідоме число буквою, наприклад х. - Виділи зв’язки невідомого з іншими числовими даними задачі. Нагадайте, що відбулося з цим числом? (Число х помножили на 4 і отримали 28.) - Складемо рівняння. Запишімо це. (х . 4 = 28) - Що ми отримали? (Рівняння.) Розв’яжемо рівняння і дізнаємося про шукане число. - Прочитайте рівняння. Що невідомо? (Невідомий перший множник.) - Як знайти перший множник? (Щоб знайти перший множник, треба добуток поділити на другий множник.) - Виконайте дії. (х = 28: 4 х = 7) Зазначимо, що при розв’язання задач способом складання рівняння, у рівняннях перевірку не робимо. - Запишіть відповідь.(Відповідь: 7 – невідоме число.) Отже, задачі на знаходження невідомого множника розв’язуються способом рівняння, тому її опорна схема:
Таким чином, якщо в задачі говориться про невідоме число, яке збільшили, зменшили, або помножили, то цю задачу треба розв’язувати способом складання рівняння за даною пам’яткою. Аналогічно складається методика підготовчої роботи і ознайомлення с задачами на знаходження невідомого діленого та невідомого дільника.
17.Задачі з пропорційними величинами.
Задачі з пропорційними величинами вводяться тоді, коли учні вже добре засвоїли конкретний зміст дій множення і ділення. Але, між тим, вони стикаються з певними труднощами, щоразу зустрічаючись з новими величинами. Виходячи з цього, вважаємо необхідним спеціально відводити час для ознайомлення школярів з пропорційними величинами. Отже, радимо познайомити учнів з групами пропорційних величин: - маса 1 предмета, кількість предметів, загальна маса, - об’єм однієї посудини, кількість посудин, загальний об’єм, - довжина 1 відрізу, кількість відрізів, загальна довжина, - ціна, кількість, вартість, - продуктивність праці, час роботи, загальний виробіток; - витрата на 1...., кількість...., загальна витрата; - швидкість, час, відстань. та зв’язками між ними. Ознайомлення з пропорційними величинами здійснюється засобом розв’язування простих задач, які спочатку розв’язуються на підставі конкретного змісту арифметичних дій множення або ділення; і лише потім можна ввести назви величин, а аналізуючи розв’язок вивести правило знаходження числового значення однієї величини за двома відомими числовими значеннями інших величин. Наприклад, розглянемо, як вводиться поняття “загальна маса”. Учням пропонується розв’язати задачу: “Мама купила на базарі 2 кг огірків, 1 кг помідорів та 3 кг картоплі. Знайдіть масу всіх овочів.”; намалюйте цю задачу, обведіть замкненою кривою лінією, що ви будете визначати. як можна дізнатися про масу всіх овочів? (Слід додати: 2+ 1 + 3 = 6 (кг) - всього овочів купила мама) Масу всіх овочів можна назвати “ загальна маса овочів”. Потім умова задачі змінюється: “Мама купила 3 пачки сілі по 1 кг кожна, знайдіть загальну масу солі.” Намалюйте задачу. Порівняйте ці задачі? Чим вони схожі? (В обох задачах йдеться про масу декількох предметів і треба знайти загальну масу.) Чим вони відрізняються? (В першій задачі говориться про предмети, що мають різну масу, а в другій – про предмети, що мають однакову масу.) Як можна знайти загальну масу однакових предметів – однакових пачок солі? (Щоб визначити загальну масу солі можна додати: 1 + 1 + 1 = 3 (кг) – загальна маса солі; але тут маємо суму однакових доданків, а в математиці суму однакових доданків називають множенням, тому цю задачу можна розв’язати дією множення: 1 * 3 = 3 (кг) – загальна маса солі.) - Уважно розгляньте останню рівність. Що означає число 1? (Маса однієї пачки солі.) Що означає число 3? (Скільки купили пачок солі.) Як це можна інакше сказати? “Скільки предметів?” – це кількість предметів. Виходячи з цього, розкажіть правило про те, як дізнатися про загальну масу декількох однакових предметів. (Щоб знайти загальну масу декількох однакових предметів, треба масу одного предмету помножити на кількість предметів.) - Чому дорівнює загальна маса декількох предметів? (Загальна маса декількох предметів дорівнює сумі мас цих предметів. Якщо предмети мають однакову масу, то загальна маса дорівнює добуткові маси одного предмету на кількість цих предметів.)
Аналогічно можна ввести величини: “загальна довжина”, “довжина 1 відрізу”, “кількість відрізів”. 1. Кравчиня відрізала від рулону тканини 3м на пальто і 2 м на костюм. Скільки всього метрів тканини відрізала від рулону кравчиня? Яку загальну довжину тканини відрізала кравчиня від рулону? 2. Кравчиня відрізала від рулону тканини на 3 плаття по 2 метри. Скільки всього метрів тканини відрізала від рулону кравчиня? Яку загальну довжину тканини відрізала кравчиня від рулону?
Також на підставі порівняння і розв’язання простих задач можна ввести поняття “загальний об’єм”, “об’єм 1 посудини”, “кількість посудин”: 1. Селянка продала на ринку 2 л та 3 л молока. Скільки всього літрів молока продала на ринку селянка? Який загальний об’єм молока продала селянка? 2. Селянка продала на ринку 3 банки по 1л молока. Скільки всього літрів молока продала на ринку селянка? Який загальний об’єм молока продала селянка?
Далі усі ці правила можна узагальнити: - Як назвати одним словом масу, довжину та об”єм? (Величини) Яка спільна властивість притаманна цим величинам? (Загальне значення кожної величини для декількох предметів дорівнює сумі значень величин, притаманним цим предметам. А якщо дані предмети мають
Потім треба обговорити питання про залежність загальної величини від зміни однієї з двох інших величин. Наприклад: - Порівняй ці задачі з попередніми. Переформулюйте запитання задач. Розв’яжіть їх усно: 1. Батько приніс дві сітки по 4 кг картоплі. Скільки всього кілограмів картоплі приніс батько? 2. Колгоспниця від чотирьох кіз надоїла по 3 л молока. Скільки всього літрів молока надоїла від із колгоспниця? 3. Для виготовлення закладок дівчина відрізала від рулону 4 рази по 2 дм стрічки. Скільки всього дециметрів стрічки витратила дівчинка на закладки? - Що станеться з загальною масою картоплі, якщо кількість сіток збільшиться? Зменшиться? - Що станеться з загальним об’ємом, якщо кількість кіз, що доїла господарка збільшиться? Зменшиться? - Що станеться з загальною довжиною, якщо кількість відрізів збільшиться? Зменшиться? - Що станеться з загальним значенням величини, якщо кількість збільшиться? Зменшиться? - Що повинно статися, щоб загальне значення величини збільшилося? Зменшилося? (Щоб збільшилося (зменшилося) загальне значення величини повинна збільшитися (зменшитися) кількість) - Що ще може статися, що
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1031; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.03 с.) |



 П –?, у разів б (м.)
П –?, у разів б (м.)
 А В
А В




 ?
?













 1 –
1 – у?
у? Чи можна відповісти на запитання задачі відразу? (Можна, тому що нам відомі обидва числові значення.)
Чи можна відповісти на запитання задачі відразу? (Можна, тому що нам відомі обидва числові значення.)




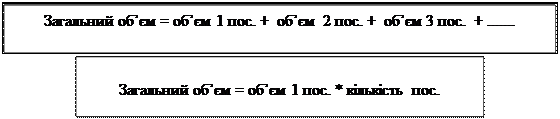
 однакові значення величини, то загальне значення величини дорівнює добуткові значення даної величини на кількість предметів.)
однакові значення величини, то загальне значення величини дорівнює добуткові значення даної величини на кількість предметів.)






