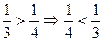Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика вивчення частин величини.
Потреба в більш точних вимірюваннях величин призвела до того, що одиниці вимірювання стали ділити на кілька рівних частин: 2, 4, 8 і так далі. Кожна частина початкової мірки мала свою назву. Наприклад, в стародавній Русі половину називали полтиною, четверту частину називали четь, про восьму частину говорили – півчеть, про шістнадцяту – півпівчеть і так далі. Рівні частини цілої мірки називали долями (частинами): четверта частина, восьма, шістнадцята й тощо. Отже, дроби – це числа, які виражають частини рахунку або вимірювання. Означення. Звичайні дроби – це числа виду, де а і в натуральні числа. Згідно програми початкового курсу математики при вивченні частин величини розв’язуються наступні задачі: 1) сформувати у учнів уявлення про частини величини; 2) навчити порівнювали частини на наочній основі; 3) навчити розв’язувати задачі на знаходження частини від числа і числа за величиною його частини. Тема “Частини величини” (“Долі”) починає вивчатися в 3-му класі під час вивчення таблиць множення і ділення. Тема вивчається на практичній основі з застосуванням великої кількості наочності: рисок паперу, прямокутників, кругів, рівносторонніх трикутників, а також можна застосовувати яблуко, торт для ділення на рівні частини.
Ознайомлення з поняттям про частини.
Учитель приносить на урок яблуко і розрізає його на дві рівні частини і показує одну таку частину. - Як можна назвати цю частину яблука?(Діти кажуть, що це половина яблука.) - Чому? (Яблуко розділили навпіл.) - Як отримати половину яблука? (Треба ціле яблуко поділити на дві рівні частини і взяти лише одну таку частину.) Учитель показує іншу частину яблука: - Що це? (Половина яблука!) Доведіть. (Яблуко поділили на дві рівні частини. Кожна така частина є половиною. Отже перша частина – половина та друга частина – половина.) - Скільки половин в цілому яблуці? (В цілому дві половини!)
- Що ви розмалювали? (Половину риски?) - Що таке половина? (Половина – це одна з двох рівних частин цілого!)
Учні розмальовують половину круга: перегинають круг навпіл так, щоб боки співпали, розгладжують лінію згину, розгортають і бачать: лінією згину поділено цілий круг на дві рівні частини; і розмальовують одну з таких частин.
Після розмалювання половини прямокутника вчитель запитує дітей: - Як отримати половину? - Поділіть прямокутник навпіл. Розмалюйте половину. - Скільки таких половин в цілому? - Як можна інакше поділити прямокутник навпіл? Покажіть половину? - Скільки таких половин в цілому? - Як інакше поділити прямокутник навпіл? Покажіть половину. - Скільки таких половин в цілому? - Скільки половин в цілому? (Цілому дві половини!)
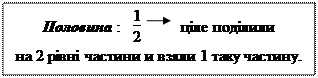
Отже, якщо цілу величину поділити на дві рівні частини, то кожну таку частину називають половиною.
- Половина - одна друга – це дробове число, воно записується так:. - Як ми отримали? (Ми одне ціле поділили на 2 рівні частини.) - Отже: 1: 2 =. - В запису під рискою записано число 2. Що означає число 2? (Число 2 означає на скільки рівних частин поділили ціле.) - Яке число записано над рискою((Число 1.) Число над рискою 1 означає скільки таких частин взяли. Деякі методисти відразу радять ввести і терміни “чисельник” і “знаменник”, тоді як за чинним підручником ці терміни вводяться при вивченні дробів в 4-му класі. - Число під рискою називається знаменник. Що показує знаменник? (Знаменник показує на скільки рівних частин поділили ціле.) - Число над рискою називається чисельник. Що показує чисельник? (Чисельник показує скільки таких частин взяли.) Отже, частини записуються парою цифр. Кажуть цифра над рискою (чисельник) та цифра під рискою (знаменник).
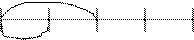
Риска – це те ж знак ділення. В математиці арифметична дія ділення має два знаки – “:”, “—“. Аналогічно вводяться третина, чверть, п’ята, шоста, восьма... частини Якщо цілу одиницю рахунку або вимірювання поділити на 3 рівні частини, то кожна буде рівна одній третій – третині:
Якщо одиницю розділити на 4 рівні частини, то кожна частина рівна одній четвертій – чверті.
Такий самий зміст мають числа,, і так далі.
Отже, запис означає, що одиницю поділили на п рівних частин і взяли 1 таку частину. Термін “ рівні частини” іноді заміняють терміном “долі” (частини). Сказати, що пиріг розділили на 5 долів – це означає, що пиріг поділили на 5 рівних частин. Закріплення поняття про частини відбувається на підставі завдань:
Завдання 1. Диню поділили порівну між 5 дітьми. Яку частину дині отримав кожний?
Завдання 2. Яку частину відрізку АВ складає відрізок СD? А С D В
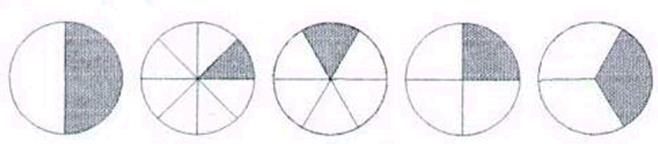
Завдання 3. Яку частину круга складає розмальована частина?
Завдання 4. Прочитай записи: торту, яблука, гарбуза, дороги, дециметру, години, кілограму. Що вони означають?
Завдання 5. Одне ціле – одиницю поділили на 7, 13, 17, 24, 99 рівних частин. Як назвати одну з таких частин в кожному випадку? Запишіть отримані дроби.
Завдання 6. Кавун важить 6 кг. Скільки кілограмів важить його половина? При розв’язанні подібних задач діти повинні міркувати за правилом: щоб отримати половину, треба ціле поділити на дві рівні частини. Отже, цілий кавун, 8 кг, треба поділити на 2. Маємо 8: 2 = 4(кг). Половина кавуна важить 8 кг.
Завдання 7. П’ята частина учнів класу відмінники. Відмінників 7 учнів. Скільки учнів в класі? При розв’язанні цього завдання учні міркують за правилом: в цілому 5 п’ятих частин, тому по 7 учнів треба взяти 5 разів. Маємо 7 * 5 = 35 (уч.). Відповідь: 35 учнів в класі.
Треба зазначити, що 6 та 7 завдання можна розглядати, як підготовку до введення правил на знаходження долі від числа та числа за його долею. З цією метою корисні запитання: - У скільки разів (,,,,...) менше за ціле? - У скільки разів ціле більше за (,,...)? Завдання 8. Яку частину метра складає 1 дм? 1 см? Яку частину години складає 1 хвилина? 1 секунда? Міркуємо так: в 1 метрі 10 дециметрів, тому 1 така частина – це, отже 1 дм – м. Порівняння частин.
Діти порівнюють частини спираючись на наочність. 1) виконують практичні дії з наочністю: на однакових геометричних фігурах отримують дані частини і накладають одну на одну, і роблять висновок; 2) розглядають малюнки, на яких на однакових геометричних фігурах розмальовані певні частини, на підставі чого роблять висновок.
Завдання 1. Порівняйте за малюнками частини: - Розгляньте риски. Що в них спільного? - На скільки рівних частин поділено першу риску? Яку частину розмальовано? Скільки половин в цілому? - На скільки рівних частин поділено другу риску? Яку частину розмальовано? Скільки третин в цілому? - На скільки рівних частин поділено третю риску? Яку частину розмальовано? Скільки четвертих частин в цілому? - На скільки рівних частин поділено четверту риску? Яку частину розмальовано? Скільки п’ятих частин в цілому? - Порівняйте та. Чому половина більша за третину? (Тому що цілу риску спочатку поділили лише на дві рівні частини, а потім – на три рівні частини; і від цього величина однієї частини зменшилася.)
- Порівняйте та. Чому? - Порівняйте та. Чому?
> > >; Величина однієї долі більше, якщо ціле поділили на менше число рівних частин. Величина однієї долі менше, якщо ціле поділили на більше число рівних частин. Завдання 2. Запишіть частини в порядку зростання:,,,,,. Завдання 3. Порівняйте половину та чверть. Що більше?
Знаходження частини (долі) від числа.
Правило знаходження частини від числа може бути введено двома способами:
Розглянемо обидві методики:
Задача1. Відрізок, довжиною 12 см розділили на 4 рівні частини. Як називається одна така частини? Знайдіть довжину четвертої частини відрізка. Доцільно розв’язання задачі ілюструвати кресленням:
12 см - Як отримати чверть? (Треба величину цілого поділити на 4 рівні частини.) Звідти витікає розв’язок: 12: 4 = 3 (см) Можна міркувати інакше: - Скільки четвертих частин в цілому? (Чотири) - У скільки разів довжина чверті менше, ніж довжина цілого відрізку? (В чотири рази.) - Якою арифметичною дією знаходимо число, яке у кілька разів менше за дане? (Дією ділення.) Розв’язання: 12: 4 = 3 (см) Відповідь: 3 см. - Що означає число 12? (Довжину цілого відрізка.) - Що означає число 4? (Кількість рівних частин в цілому.) - Що означає число 3? (Довжину четвертої частини відрізку.) - Якою арифметичною дією ми дізналися про частину від цілого? (Дією ділення) - Як знайти величину частини від цілого? (Треба величину цілого поділити на кількість рівних частин в ньому.) - Зробимо узагальнюючий висновок: Щоб знайти частину від числа, треба величину цілого поділити на кількість рівних частин в ньому.
При виведенні цього висновку можна застосовувати практичну роботу. Дітям роздаються по 3 риски паперу довжиною 24 см. Діти отримують,, цієї риски і вимірюють лінійкою довжини отриманих частин. Дані заносять у таблицю:
Діти вивчають дані таблиці і визначають, якою арифметичною дією можна дізнатися про величину частини від цілого. Потім роблять перевірку своєї гіпотези і формулюють правило.
На етапі закріплення правила учням пропонуються завдання на знаходження частини від числа: 1) Знайти від 49; 2) Знайти від 20; 3) Знайти від 100 см; 4) Знайти від 15 хв.; Задача 2. В магазин привезли 56 кг огірків. До обіду продали всіх огірків. Скільки кілограмів огірків продали до обіду?
- Що означає число 56? (Масу усіх огірків, що привезли.) - Що означає число? (Яку частину огірків продали до обіду.) - Що означає знаменник 8? (Що усі 56 кг огірків поділили на 8 рівних частин.) - Що означає чисельник 1? (ЩО 1 таку частину продали до обіду.) - Що в цій задачі грає роль цілого? (56 кг огірків). Ціле в математиці позначається, як 1. Запишімо це: - Що треба знайти в цій задачі? (Треба знайти від 56 кг.) - Як знайти частину від числа? Розв’язання: 56: 8 = 7 (кг). Відповідь: 7 кг огірків продали до обіду. Далі розв’язуються складені задачі, які містять знаходження частини від числа.
Знаходження числа за величиною його частини (долі).
Задача 1. Довжина чверті відрізка дорівнює 3 см. Визначити довжину цілого відрізка. - Скільки четвертих частин в цілому? (Чотири) - Яка довжина чверті відрізка? (3 см). - Якщо в цілому відрізку 4 таких частини по 3 см, то треба по 3 см взяти 4 рази. - Якою арифметичною дією дізнаємося про довжину цілого відрізка? (Дією множення.) Розв’язання: 3 * 4 = 12 (см). Відповідь: 12 см. - Що означає число 3? (Довжини однієї частини.) - Що означає число 4? (Кількість частин в цілому.) - Що означає число 12? (Величину цілого) - Якою дією ми дізналися про величину цілого? (Дією множення.) - Як знайти величину цілого за величиною його частини? (Треба величину частини помножити на кількість частин в цілому.) - Зробимо узагальнюючий висновок: Щоб знайти число за величиною його частини, треба величину частини помножити на кількість частин в цілому. На етапі закріплення правила учням пропонуються завдання на знаходження цілого числа за величиною його частини, наприклад: 1) Знайти число, якщо його складає 8; 2) Знайти число, якщо його дорівнює 5; 3) частина складає 7 кг. Яка маса цілого?
- Що означає число 12? (Скільки сторінок прочитала дівчинка.) - Що ще означає число 12? (Величину книги.) - Що означає число? (Яку частину книги прочитала дівчинка.) - Що означає знаменник 5? (На скільки рівних частин поділили цілу книгу.) - Що означає чисельник 1? (Скільки таких частин прочитала дівчинка.) - Що треба знайти в цій задачі? (Величину цілої книги.) - Як в математиці позначається ціле? (1) - Що треба знайти в цій задачі? (Треба знайти число за величиною його частини.)
- Як знайти число за величиною його частини? Розв’язання: 12 * 5 = 60 (с.) Відповідь: 60 сторінок в книзі.
Складені задачі, які містять знаходження частини від числа ми розглянемо в розділі „ Методика роботи над складеними задачами в 3-му класі.”.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.211.66 (0.118 с.) |

 Далі учням пропонується взяти риску паперу, поділити її на дві рівні частини і розмалювати одну таку частину.
Далі учням пропонується взяти риску паперу, поділити її на дві рівні частини і розмалювати одну таку частину.






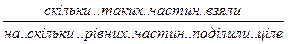
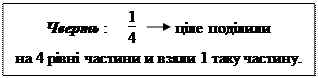









 - «одна третя»
- «одна третя»