Задачі на знаходження дати закінчення події

Задача 2. Перерва розпочалася о 9 год 15 хв і тривала 10 хв. Коли закінчилася перерва?

+

Дата початку події	Тривалість події	Дата закінчення події
9 год 15 хв	10 хв	?

 

 

 

Задачі на знаходження дати початку події.

Задача 3. Перерва тривала 30 хв і закінчилася о 10 год 35 хв. Коли розпочалася перерва?

-

Дата початку події	Тривалість події	Дата закінчення події
?	10 хв	10 год 35 хв

Щоб знайти дату початку події, треба від дати закінчення події відняти тривалість події.

Розв”язання 10 год 35 хв – 10 хв = 10 год 25 хв Відповідь: о 10 год 25 хв розпочалася перерва.

 

Розглянемо задачу: Уроки в школі починаються в 8 год. Тривалість уроків 4 год. У скільки годин закінчуються заняття?

Дата початку події	Тривалість події	Дата закінчення події
8 год.	4 год.	?

- Що означає число 8? (Час початку занять у школі.)

- Що означає число 4? (Тривалість уроків.)

- Яке запитання в задачі? (У скільки годин закінчуються заняття?)

- Що треба знати, щоб відповісти на запитання задачі? (Треба знати два числові значення: час, у якому починаються заняття, відомо – 8 год., та скільки годин тривають заняття, відомо – 4 год.)

- Якою арифметичною дією відповімо на запитання задачі? (Дією додавання.)

- Чи можна відразу відповісти на запитання задачі? (Так, відомі обидва числові значення.)

Розв’язання: 8 + 4 = 12 (год.)

Відповідь: о 12 годині закінчуються заняття.

Складаємо обернені задачі.

8, 4,

- пряма задача.

 

, 4, 12. – 1-ша обернена задача.

 

Уроки в школі тривають 4 години і закінчуються о 12 годині. О котрій годині розпочинаються заняття в школі?

Розв’язання: 12 – 4 = 8 год.)

Відповідь: о 8 годині розпочинаються заняття.

8,, 12 – 2 –га обернена задача.

 

Уроки в школі розпочинаються о 8 –й годині і закінчуються у 12-й годині. Скільки годин тривають заняття в школі?

Розв’язання: 12 – 8 = 4 (год.)

Відповідь: 4 години тривають заняття в школі.

 

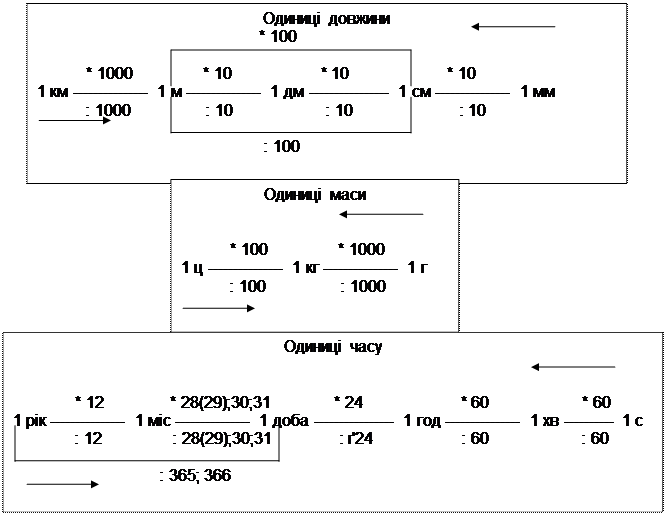
Узагальнити одиниці вимірювання величин можна на підставі таблиці:

 

 

 

 

Нестандартні задачі для 3-го класу.

 

Під нестандартними задачами ми розуміємо такі задачі, тематика яких не є сама по собі об’єктом вивчення; це не задачі, важкі для розв’язання, а задачі нестандартні за своєю тематикою.

 

Задачі, які розв’язуються способом логічних міркувань.

Задача 1. Василь, Гена та Євген змагалися у бігу. Хто з них прибіг першим, другим та третім, якщо вірні наступні твердження:

1) Василь прибіг не першим, а Євген не другим.

2) Гена прибіг не третім, а Василь не другим.

Розв’язання. Автор пропонує розв’язувати цю задачу за допомогою таблиці.

	В -     Г       Є   -

 

 

Так як усі твердження вірні, то з 1) випливає, що Василь міг прибігти або другим або третім, а Євген – або першим або третім; Василь ніяк не міг бути першим, а Євген другим. У відповідних клітинках таблиці поставлені знаки „-„.

З 2) випливає, що Євген прибіг не третім, а Василь не другим.

	В - - + Г       Є + - -

 

 

Таким чином, Василь прибіг третім, а Євген – першим. У відповідних клітинках поставимо знаки „+”. Лишається, що Гена був другим.

Відповідь: Євген прибіг першим, Гена – другим, Василь – третім.

Аналогічно, складаючи таблицю, розв’язуються наступні задачі:

Задача 2. В квартирах № 1, № 2, № 3 мешкали три кошеня: білий, чорний і рижий. В квартирах № 1 та № 2 мешкало не чорне кошеня. Біле кошеня мешкало не в квартирі № 1. В якій квартирі мешкало кожне кошеня?

Відповідь: чорне кошеня мешкало в квартирі № 3, біле кошеня – в квартирі № 2, а риже кошеня – в квартирі № 1.

Задача 3. Коли Ала, Катя і Люда спитали, які оцінки вони отримали за контрольну роботу з математики, то вчителька відповіла: „ Спробуйте здогадатися самі, а вам скажу, що в класі двійок немає і у вас трьох різні оцінки, при чому у Али не „3”, у Люди не „3” і не „5”. Напиши, яку оцінку отримала кожна з трьох учениць.

Відповідь: у Люди – „4”, у Али – „5”, у Каті – „3”.

Задача 4. Микола, Петро, Іван збирали гриби. Микола знайшов 10 сироїжок і стільки білих, скільки підберезників знайшов Іван. Іван знайшов лисичок в 2 рази менше, ніж сироїжок Микола, і 3 підберезники. Петро знайшов лише лисички, який в нього було більше, ніж білих у Миколи, але менше, ніж лисичок у Івана. Скільки грибів зібрали хлоп’ята, якщо відомо, що Микола знайшов лише сироїжки та білі, а Іван – підберезники і лисички?

Розв’язання. Так як Микола знайшов 10 сироїжок, а Іван в 2 рази менше лисичок, то Іван знайшов 10: 2 = 5 лисичок. Іван знайшов 3 підберезників, а Микола стільки ж білих, тому Микола знайшов 3 білих.

Петро знайшов лише лисички, який в нього було більше, ніж білих у Миколи, але менше, ніж лисичок у Івана. Тому Петро знайшов лисичок більше 3, але менше 5 – це 4. Петро знайшов 4 лисички. Отже хлоп’ята всього знайшли: 10 + 5 + 3 + 3 + 4 = 25 грибів.

Задача 5. Ігор, Петро і Сашко ловили рибу. Кожний з них спіймав або йоржів або піскарів, або окунів. Хто з них спіймав яких риб, якщо відомо, що:

1) Колючі плавники є в окунів та йоржів, а в піскарів немає.

2) Ігор не спіймав жодної риби з колючими плавниками.

3) Петро спіймав на 2 окуні більше, ніж спіймав риб Ігор.

Скільки риб спіймав кожний хлопчик, якщо Ігор спіймав 3 риби, а всього риб було менше 10?

Розв’язання. Відомо, що Ігор не спіймав жодної риби с колючими плавниками, значить він спіймав лише піскарів. З третьої умови ясно, що Петро наловив окунів. Тому Сашко спіймав лише йоржів.

Відомо, що Ігор спіймав 3 риби – 3 піскаря. Петро спіймав на 2 окуні більше, ніж спіймав риб Ігор: 3 + 2 = 5 окунів спіймав Петро.

Маємо, що Петро і Ігор разом спіймали 5 + 3 = 8 риб. Отже, три хлопчики спіймали більше, ніж 8 риб, але менше за 10. Значить три хлопчики спіймали 9 риб. Значить Сашко спіймав 1 йоржа.

 

Задача 6. Гном розклав свої скарби а 3 сундука різного кольору, які стояли у стіни: в один – коштовні каміння, в другий – золоті монети, в третій – магічні книги. Він пам’ятає, що червоний сундук знаходиться правіше, ніж каміння, і що книги – правіше червоного сундука. В якому сундуку лежать книги, якщо зелений сундук стоїть лівіше синього?

Розв’язання. За умовою сундук з камінням лівіше червоного, а сундук з книжками правіше червоного. Тому червоний сундук стоїть між сундуком з камінням і сундуком з книгами, і в ньому лежать золоті монети. Крім того, червоний сундук правіше від сундука з каміннями, тому сундук з камінням стоїть зкраю зліва; книги правіше червоного сундука, тому сундук з книгами стоїть зкраю справа.

	каміння		Червоний- монети		книги

 

Так як зелений і синій сундук – зкраю і за умовою зелений стоїть лівіше синього, то синій стоїть зкраю зліва, а зелений зкраю справа:

	зелений каміння		Червоний- монети		синій книги

Відповідь: в синьому.

 

Задача 7. Дві мухи змагаються у бігу. Вони біжать з пола до стелі і повертається. Перша муха біжить в обидві сторони з однаковою швидкістю. Друга муха біжить вниз вдвічі швидше, ніж перша, а вверх – вдвічі повільніше, ніж перша. Хто з мух переможе?

Розв’язання. Нехай мухи долають перший етап – від полу до стелі. Перша муха вже добіжить до стелі, а друга добіжить тільки до половини шляху.

 

1 муха.

 

2 муха.

 

Перша муха повертається до полу, а друга – лише добирається до стелі. Перемагає перша муха. Помітимо, не має значення, у скільки разів швидше буде бігти вниз друга муха, ніж перша.

Відповідь: перша.

 

Задачі, пов’язані з нумерацією чисел.

Задача 8. В потязі 14 вагонів. Хлопчик сів в сьомий вагон. Скільки вагонів попереду цього вагона и скільки вагонів позаду?

Розв’язання. Спереду 6 вагонів, а позаду 14 – 7 = 7 (вагонів).

Задача 9. В потязі 11 вагонів. Наш вагон восьмий, якщо вести рахунок від голови потягу. Яким є цей вагон, якщо рахувати від хвоста потягу?

Розв’язання. 11 – 8 = 3 – число вагонів, які знаходяться позаду 8-го вагона. Шуканий номер буде на 1 більшим. Маємо: (11 – 8) + 1 = 4 - четвертий номер.

1, 2, 3, 4, 5, 6, 7, (8), 9, 10, 11.

(4),(3), (2), (1).

Задача 10. Скільки аркушів між п’ятим і вісімнадцятим аркушами альбому?

Розв’язання. (18 – 5) – 1 = 12.

Задача 11. Скільки парних чисел між числами 6 та 16?

Розв’язання. 6: 2 = 3 – порядковий номер парного числа 6 та 16: 2 = 8 – порядковий номер парного числа 16 в ряді парних чисел від 2 до 26. Маємо (8 – 3) -1 = 4 числа.

(6), 8, 10, 12, 14, (16).

Автор зазначає, що розв’язання таких задач краще записувати по-іншому:

(16 – 6): 2 – 1 = 4 (числа), де 16 та 6 – числа, які вказані в умові задачі.

Задача 12. Скільки є будинків між будинками № 36 та №56, які розташовані по одній стороні вулиці?

Розв’язання. (56 – 36): 2 – 1 = 9.

Задача 13. Скільки всього парних чисел від 4 до 16, включаючи названі числа?

Розв’язання. 4: 2 = 2 – порядковий номер числа 4 та 16: 2 = 8 – порядковий номер числа 16 в ряді парних чисел від 4 до 16. Маємо: (8 – 2): 2 + 1 = 7 (чисел).

(4), 6, 8, 10, 12, 14, (16).

Розв’язання таких задач краще записувати по-іншому: (16 – 4): 2 + 1 = 7, де 16 та 4 – дані в умові задачі числа.

Задача 14. Скільки будинків на одній стороні вулиці від № 16 до № 36, включно?

Розв’язання. (36 – 16): 2 + 1 = 11

Задача 15. Сходи складаються з 7 сходинок. Яка за номером сходинка знаходиться по середині сходів?

Розв’язання. Задача призводиться до знаходження числа, яке знаходиться посередині числового ряду:

1, 2, 3, (4), 5, 6, 7.

Так як, число 7 – непарне, то в середині цього числового ряду буде знаходитися лише одне число: 7: 2 = 3 (остача 1). Зліва і справа від шуканого числа будуть по 3 числа в ряду чисел від 1 до 7. Шуканим є число, яке прямує за числом 3.

Маємо: 3 + 1 = 4 (середнє число).

Розв’язання таких задач краще записувати по-іншому: (7 + 1): 2 + 4 – середньою буде четверта сходинка.

Задача 16. У залізничному потязі 9 вагонів. Який вагон займає середину потягу?

Розв’язання. (9 + 1): 2 = 5 (п’ятий).

Задача 17. Сходи містять 8 сходинок. Які сходинки займають середню частину сходів?

Розв’язання. Так як 8 – число парне, то задача призводиться до знаходження двох чисел, що знаходяться посередині числового ряду:

1, 2, 3, (4), (5), 6, 7, 8.

Маємо: 8: 2 = 4 та 4 + 1 = 5 – середніми є четверта та п’ята сходинки.

Задача 18. В потязі 16 вагонів. Які вагони знаходяться в середині потягу?

Розв’язання. 16 6 2 = 8 – восьмий вагон та 8 + 1 = 9 – дев’ятий.

Задача 19. Перше календарне число, що приходиться на вівторок, є 4. Які ще календарні числа приходяться на вівторок в цьому місяці?

Розв’язання. Кожний наступний вівторок є сьомим днем після попереднього вівторку.

Маємо 4 + 7 = 11, 11 + 7 = 18 та 18 + 7 = 25.

Задача 20. На середу приходяться календарні числа: 5, 12, 19, 26. які календарні числа приходяться на суботу?

Розв’язання. 6 – 3 = 3 – субота, шостий день тижня - є третім днем після середи (третього дня тижня).

Маємо: 5 + 3 = 8, 12 + 3 = 15, 19 + 3 = 22 та 26 + 3 = 29.

Задача 21. На неділю приходиться календарні числа: 9, 16, 23, 30. Які календарні дні приходяться на вівторок в цьому місяці?

Розв’язання.

7 – 2 = 5 – вівторок (другий день тижня) є п’ятим днем, що передують неділі (сьомому дню тижня).

Маємо: 9 – 5 = 4, 16 – 5 = 11, 23 – 5 = 18, 30 – 5 = 25.

Задача 22. Скільки всього двоцифрових чисел, трицифрових чисел?

Розв’язання. 9 – число одноцифрових чисел, 99 – число одноцифрових та двоцифрових чисел, 999 – число одноцифрових, двоцифрових та трицифрових чисел.

Маємо 99 – 9 = 90 – двоцифрових чисел та 999 – 99 = 900 – число трицифрових чисел.

 

Задачі, які розв’язуються міркуванням за допомогою схематичного малюнка.

Задача 23. В бібліотеці на двох полицях по 15 книжок. До обіду з однієї полиці взяли кілька книг, а після обіду з іншої полиці взяли стільки книжок, скільки залишилося на першій полиці. Скільки книжок залишилося на обох полицях?

Задача 24. В двох вагонах їхали пасажири, по 36 людин в кожному. На станції з першого вагону вийшло кілька людей, а з другого вагону вийшло стільки, скільки залишилося в першому. Скільки всього пасажирів залишилося в двох вагонах?

Розв’язання. Позначимо кількість людей в кожному вагоні відрізками однакової довжини (їх за умовою було по 36 людей) і потім показати на кожному відрізку тих пасажирів, які вийшли з одного й іншого вагону, то можна дуже легко відповісти на запитання.

вийшло

1 вагон

вийшло

2 вагон

Відповідь: 36 людей.

Задача 25. В бібліотеці на двох полицях по 15 книжок. До обіду з однієї полиці взяли кілька книг, а після обіду з іншої полиці взяли стільки книжок, скільки залишилося на першій полиці. Скільки книжок залишилося на обох полицях?

Відповідь: 15 книжок.

Задача 26. В двох коробках по 20 цукерок. Ласунка Маша з’їла кілька цукерок з першої коробки. Побачивши це, ласунка Оленка з’їла з другої коробки стільки цукерок, скільки залишилося в першій. Скільки цукерок залишилося після цього в обох коробках?

Відповідь: 20 цукерок.

 

Задачі, які розв’язуються арифметичним методом.

Задача 27. В двох коробках 22 олівця. В першій коробці на 2 олівця більше, ніж в другій. Скільки олівців в кожній коробці?

Розв’язання.

1 коробка

2 22

2 коробка

1 спосіб:

1) 22 – 2 = 20 (шт..) олівців було б в двох коробках, якби в них олівців було порівну.

2) 20: 2 = 10 (шт..) олівців було б в двох коробках, якби в них олівців було б порівну; стільки олівців в другій коробці.

3) 10 + 2 = 12 (шт..) олівців в першій коробці.

2 спосіб:

1) 22 + 2 = 24 (шт..) – подвоєне число олівців в 1-й коробці;

2) 24: 2 = 12 (шт..) олівців в 1-й коробці;

3) 12 – 2 = 10 (шт..) олівців в 2-й коробці.

Відповідь: 12 олівців, 10 олівців.

 

Задача 28. Пояс з пряжкою коштує 12 грн., при чому пояс дорожчий за пряжку на 6 грн. Скільки коштує пояс, скільки коштує пряжка?

Розв’язання:

1) 12 – 6 = 6 (грн..) коштував би пояс з пряжкою, якби вони мали однакову ціну;

2) 6: 2 = 3 (грн..) коштує пряжка;

3) 3 + 6 = 9 (грн..) коштує пояс.

Відповідь: 9 гривень., 3 гривні.

 

Задача 29. В двох кошиках 75 яблук. Коли з першої взяли 6, а з другої 9, то в кошиках лишилося яблук порівну. Скільки яблук було в кожному кошику?

Розв’язання.

1 кошик

6 75

2 кошик

1 спосіб.

1) 6 + 9 = 15 (ябл.) – стільки яблук взяли з двох кошиків.

2) 75 – 15 = 60 (ябл.) - всього в двох кошиках, коли в них стало яблук порівну.

3) 60: 2 = 30 (ябл.) – стало в кожному кошику.

4) 30 + 6 = 36 (ябл.) – було в першому кошику.

5) 30 + 9 = 39 (ябл.) – було в другому кошику

2 спосіб.

1) 75 – 6 = 69 (ябл.) - стало в двох кошиках, після того, як з першого кошика взяли 6 яблук.

2) 69 – 9 = 60 (ябл.) – стало в двох кошиках, після того, як взяли 9 яблук з другого кошика.

3) 60: 2 = 30 (ябл.) – стало в кожному кошику.

4) 30 + 6 = 36 (ябл.) – було в першому кошику.

5) 30 + 9 = 39 (ябл.) – було в другому кошику.

Відповідь: 36 яблук, 39 яблук.

Задача 30. В двох коробках – 84 цукерки. Коли з першої коробки взяли 44 цукерки, а другої 30 цукерок, то в них залишилося цукерок порівну. Скільки цукерок було в кожній коробці спочатку?

Треба зазначити, що автор не наводить схематичного малюнка цієї задачі, але ми вважаємо його дуже корисним для знаходження способу її розв’язання:

1 коробка

44 84

2 коробка

 

Розв’язання. З двох коробок взяли 44 + 30 = 74 цукерки. Значить в двох коробках залишилося: 84 -74 = 10 цукерок. Так як в двох коробках залишилося цукерок порівну, то в кожній з них залишилося 10: 2 = 5 цукерок. Отже в першій коробці було 5 + 44 = 49 цукерок, а в другій – 30 + 5 = 35 цукерок.

Відповідь: 49 цукерок, 35 цукерок.

Задача 31. У двох хлопчиків було разом 8 груш. Коли один хлопчик з’їв одну грушу, а інший 3 груші, у них залишилося груш порівну. Скільки груш було у кожного?

Відповідь: 3 груші і 5 груш.

 

Задача 32. Було 10 гномів в білих, синіх та коричневих ковпачках. Гномів в синіх ковпачках було в 2 рази менше, ніж в коричневих, а решта гномів були в білих ковпачках. Скільки було гномів в білих, синіх та коричневих ковпачках, якщо в білих ковпачках їх було стільки ж, скільки і в коричневих?

Треба зазначити, що цю задачу можна розв’язати арифметичним способом, якщо скласти схематичний малюнок:

 

Б.

 

К. 10 шт.

 

С.

 

Маємо всього 5 рівних частин. Щоб дізнатися. Скільки ковпачків в одній такій частині, треба:

1) 10: 5 = 2 (шт.) ковпачків в меншій частині, тому 2 синіх ковпачки.

2) 10 – 2 = 8 (шт.) білих і коричневих ковпачків.

3) 8: 2 = 4 (шт.) білих або коричневих ковпачків.

Відповідь: 4 гнома в білих ковпачках, 4 гнома в коричневих ковпачках, 2 гнома в синіх ковпачках.

Задача 33. У п’ятьох селян – Івана, Петра, Якова, Михайла і Герасима було 10 овець. Не могли вони знайти пастуха, щоб пасти овець. І каже Іван: „ Будемо пасти овець по черзі – по стільки днів, скільки кожний з нас має овець”. Пол скільки днів повинен кожний селянин пасти овець, якщо відомо, що у Івана в 2 рази менше овець, ніж у Петра, у якова в 2 рази менше овець, ніж у Івана; Михайло має овець в 2 рази більше, ніж Яків, а Герасим – в четверо менше, ніж у Петра?

Розв’язання.

І.

 

П.

 

Я. 10 ов.

 

М.

 

Г.

 

10: 10 = 1 – було овець у Герасима або у Якова;

1 х 2 = 2 – було овець у Михайла або у Івана;

2 х 2 = 4 – було овець у Петра.

Відповідь: у Івана – 2 овець, у Петра – 4 вівці, у Якова – 1 вівця, у Михайла – 2 вівці, у Герасима – 1 вівця.

Задача 34. У Московському Кремлі зберігаються старовинна грамота і дзвін. За величину їх назвали цар - дзвоном і цар-грамотою. Їх загальна маса 240 т. Цар-дзвін в 5 разів важчий, ніж цар-грамота. Яка маса цар-дзвона і цар-грамоти окремо?

Відповідь: 40 т маса цар-грамоти і 200 т – маса цар – дзвону.

Задача 35. Портфель та чотири пари черевиків коштують 27 карбованців. Пара черевиків дорожче, ніж портфель у 2 рази. Скільки коштує пара черевиків?

Відповідь: 3 карбованці коштує портфель і 6 карбованців коштує пара черевиків.

 

Задача 33.Накреслити два відрізка так, щоб один був довший іншого на чверть, а разом вони складали б відрізок, довжиною 18 см.

Розв’язання. Довше другого відрізку на чверть, треба розуміти як на чверть довше, ніж саме другий:

 

1.

18 м

П.

 

Маємо в двох відрізках 9 рівних частин. 18: 9 = 2 см – в одній частині. 2 * 4 = 8 см – довжина другого відрізку. 2 * 8 = 10 см – довжина першого відрізка.

Відповідь: 10 см і 8 см.

Задача 36. Пес Тузик на 12 кг важче за кота Барсика, а Барсик вчетверо легше Тузика. Скільки важить Барсик?

Розв’язання. Якщо Барси в четверо легший за Тузика, то Тузик в четверо важчий за Барсика. Зробимо схематичний малюнок: накреслимо два відрізка, один з них в 4 рази довший за інший і позначимо їх різницю числом 12:

Т.

 

 

Б.

 

В першому відрізку чотири однакові частини, в другому – одна така частина. В першому відрізку три частини дорівнюють 12 кг. Отже, в одній такій частині 12 кг: 3 = 4 кг.

Відповідь: 4 кг (20).

Задача 37. Мама подала до обіду 8 пиріжків. Скільки пиріжків вона спекла, якщо в мами залишилося ще стільки та півстільки?

Відповідь: 20 пиріжків.

 

Задача 38. В одному мішку 48 кг борошна, а в другому наполовину менше. Чому дорівнює чверть половини всієї муки?

Розв’язання.

Якщо в другому мішку на половину менше, ніж в першому, то в другому мішку – половина першого.

1) 48: 2 = 24 (кг) борошна в другому мішку.

2) 48 + 24 = 72 (кг) борошна в обох мішках.

Чверть половини всієї муки – це її восьма частина.

3) 72: 8 = 9 (кг) – складає чверть половини всієї муки.

Відповідь: 9 кг.

Задача 39. В одній коробці 40 цукерок, а в іншій на половину менше. Чому дорівнює половина половини усіх цукерок?

Відповідь: 15 цукерок.

Задача 40. В одній коробці 20 цукерок, а в іншій наполовину менше. Чому дорівнює половина усіх цукерок?

Відповідь: 15 цукерок.

Задача 41. В одній коробці 40 цукерок, а в іншій наполовину менше. Чому дорівнює чверть усіх цукерок?

Відповідь: 15 цукерок.

 

Задача 42.Шестеро тягнуть ріпку: дідусь вдвічі сильніше бабусі, бабуся вдвічі сильніше онучки, онучка вдвічі сильніше Жучки, Жучка вдвічі сильніше кішки, кішка вдвічі сильніше миші. Скільки треба покликати мишів, щоб вони самі витягнули ріпку?

Розв’язання. Задача розв’язується з кінця. Силу кожного учасника виразимо в мишках: кішка = 2 мишки, жучка = 4 мишки, онучка = 8 мишок, бабуся = 16 мишок, дідусь = 32 мишки. 2 + 4 + 8 + 16 + 32 = 64, отримаємо 62 мишки плюс мишка, яка згадується в умові задачі.

Відповідь: 65 мишок.

 

Задача 43. Серед 12 цуценят 8 з довгими вухами та 9 тих, що кусаються. Скільки серед цих цуценят з довгими вухами і тих, що кусаються одночасно?

Розв’язання.

1) 12 – 8 = 4 (ц.) без довгих вух.

2) 12 – 9 = 3 (ц.) не кусаються.

3) 4 + 3 = 7 (ц.) або тільки мають довгі вуха або тільки кусаються.

4) 12 – 7 = 5 (ц.) і мають довгі вуха і кусаються.

Відповідь: 5 цуценят.

Задача 44. В класі усі діти вивчають англійську та французьку мову. З них 17 учнів вивчають англійську, 15 учнів – французьку, а 8 – вивчають обидві мови одночасно. Скільки учнів в класі?

Розв’язання.

1) 17 – 8 = 9 (уч.) вивчають лише англійську мову.

2) 15 – 8 = 7 (уч.) вивчають лише французьку.

3) 9 + 7 + 8 = 24 (уч.) всього в класі

Відповідь: 24 учня.

Задача 45. В класі 25 учнів. З них 6 учнів не вміють грати або в шашки, або в шахи. 18 учнів вміють грати в шашки, 20 – в шахи. Скільки учнів класу грають і в шашки і в шахи?

Розв’язання. Відомо, що 18 учнів грають в шашки, тому 25 – 18 = 7 учнів не вміють грати в шашки. Якщо ми із 7 – 6 = 1 учнів не вміють грати в шашки, але можуть вміти грати в шахи. Так як 20 учнів вміли грати в шахи, то 20 – 1= 19 учнів могли грати і в шахи і в шашки.

Відповідь: 19 учнів.

Задача 46. Чи відомо тобі, що серед усіх порід кішок тільки гепарди не втягують кігті. Кігті, в них завжди знаружі, як у собак. Серед мешканців площадки молодняку у зоопарку 18 – котеня та щеня різних порід. З них 9 – щенят, а 13 не втягують кігті. Скільки мешканців – гепарди і скільки котенят інших порід?

Розв’язання. Серед 13 малюків, не витягують кігті, 9 –щенят, тому (13 – 9) = 4 – гепарди. Кошенят інших порід 18 – (9 + 4) = 5. Відповідь: 4 гепарди і 5 кошенят інших порід.

 

Задача 47. В одному колесі 18 зубців, а в іншому, яке зціплене з ним, 30 зубців. Перше колесо зробило 15 обертів. А друге?

Розв’язання.

 

А

 

Точка А – точка зціплення колес. В той час, коли через точку А проходить один зубець першого колеса, через цю ж точку проходить один зубець другого колеса. Отже, за один й той же час через точку А проходить однакова кількість зубців першого та другого колес.

1) Скільки зубців першого колеса пройшло через точку А за 15 обертів цього колеса? 15 х 18 = 270.

2) Скільки зубців третього колеса пройшло через точку А за цей самий час? Стільки ж, 270.

3) Скільки обертів повинно зробити друге колесо, щоб через точку А пройшло 270 його зубців? 270: 30 = 90.

Відповідь: 90 обертів.

 

Задача 48. Прийшов селянин на базар і приніс кошик яєць. Його запитали: „ Чи багато в тебе яєць в кошику?” Селянин відповів так: „ Я не пам’ятаю скільки всього в тому кошику яєць. Тільки пам’ятаю, коли я складав в кошик яйця по 2, в мене залишилося 1 яйце зайве. Тоді я став класти в кошик по 3 яйця, знов одне яйце залишилося. Якщо класти по 4 яйця, то одне яйце залишається зайвим. Якщо класти по 5 яєць в кошик, то знов одне яйце залишилося зайвим. Якщо класти по 6 яєць, то одне яйце залишається зайвим. Якщо класти по 7 яєць в кошик, жодного яйця не залишилося. Скільки було в кошику яєць?”

З умови задачі невідоме число при діленні на 2 дає остачу 1: а * 2 + 1 = х.

Невідоме число при діленні на 3 дає остачу 1: в * 3 + 1 = х.

Невідоме число при діленні на 4 дає остачу 1: с * 4 + 1 = х.

Невідоме число при діленні на 5 дає остачу 1: к * 5 + 1 = х.

Невідоме число при діленні на 6 дає остачу 1: п * 6 + 1 = х.

Таким чином, якщо невідоме число зменшити на 1, то воно ділитиметься на всі ці числа без остачі; таке число може бути отримане добутком усіх цих чисел:

2 * 3 * 4 * 5 * 6 = 720

До отриманого результату додамо 1: 720 + 1 = 721.

Число 721 ділиться на 7 без остачі, а при діленні на 2,3,4,5,6 дає остачу 1.

Відповідь: 721. Можна отримати й інші розв’язки.

 

Задача № 49. У хлопчика в колекції є жуки та павуки – всього 8 штук. Якщо перелічити усі ноги в колекції, то їх буде 54. Скільки в колекції жуків і скільки павуків?

Розв’язання. Припустимо, що в коробці були усі жуки (на дошці позначаємо комах з 6 ногами). Скільки всього в них ніг? (6 * 8 = 48) А в умові задачі всього 54 ноги. На скільки більше ніг повинно бути у комах? (54 – 48 = 6). А чому так сталося? (Тому, що в колекції, крім жуків, були й павуки, а в них ніг більше.) У павука 8 ніг, а у жука – 6. На скільки більше ніг у павука, ніж у жука? (На дві ноги.) Значить, 6 ніг треба розподілити між комахами (жуками), добавляючи кожному по 2 ноги. Павуків буде стільки, скільки в 6 міститься по 2, тобто 3.

1) 6 * 8 = 48 (ніг) всього було б, якби в колекції були лише жуки.

2) 54 – 48 = 6 (ніг) на стільки ніг більше у комах, ніж ми передбачили.

3) 8 – 6 = 2 (ноги) на стільки більше ніг у павука, ніж у жука.

4) 6: 2 = 3 – стільки жуків.

5) 8 – 3 = 5 павуків.

Можна розпочати міркування з передбачення, що в колекції були лише павуки:

1) 8 * 8 = 64 (ноги) всього, якби всі були павуки.

2) 64 – 54 = 10 (ноги) зайві

3) 8 – 6 = 2 (ноги) на стільки більше ніг у павука, ніж у жука.

4) 10: 2 = 5 – стільки павуків

5) 8 – 5 = 3 жуків.

Треба зазначити, що такі задачі розв’язуються також способом підбору.

 

Задачі, які розв’язуються способом підбору.

 

Задача 50. Для дитячого садка були закуплені іграшки: зайчики, ведмеді й слоники – всього 31 іграшка. Зайчиків було в 5 раз більше, ніж ведмедів, а слоників менше, ніж зайчиків. Скільки було куплено для дитячого садка зайчиків, ведмедів і слоників, якщо відомо, що один зайчик коштує 1 грн., ведмідь – 2 грн., слоник – 3 грн. І за всю покупку було сплачено 38 грн.?

Розв’язання. Треба розбити цю задачу на дві частини: перша частина стосується підбору кількості іграшок кожного виду, а друга – підрахунку вартості всієї покупки. Спочатку визначимо, скільки могло бути іграшок кожного виду, щоб їх загальна кількість була 31, тобто виконувалася перша умова задачі.

Будемо розв’язувати задачу підбором. Припустимо був куплений 1 ведмідь, тоді зайчиків – 5, тоді маємо, що слоників: 31 – 1 – 5 = 25; ми отримали протиріччя умові: „ слоників менше, ніж зайчиків”. Цей випадок не підходить.

Припустимо, що було куплено 2 ведмедя, тоді зайців – 10, а слоників: 31 – 2 – 10 = 19. Знов отрима